方腔内自然对流的格子玻尔兹曼模拟毕业论文
2020-06-20 19:26:04
摘 要
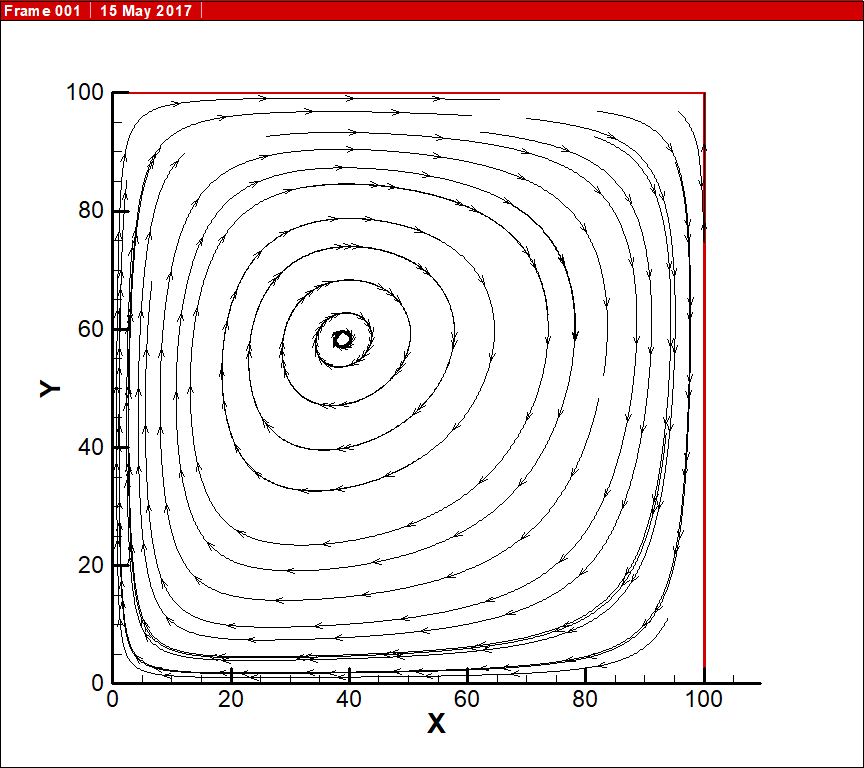
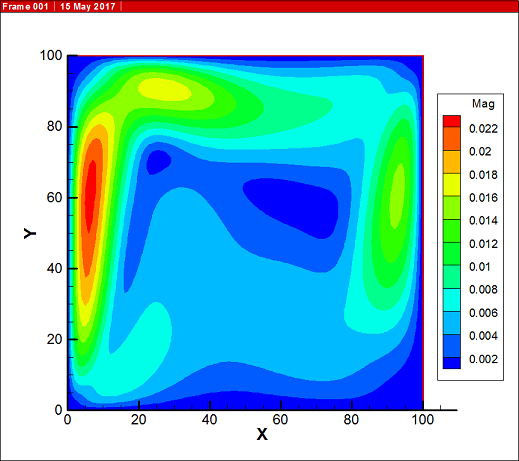
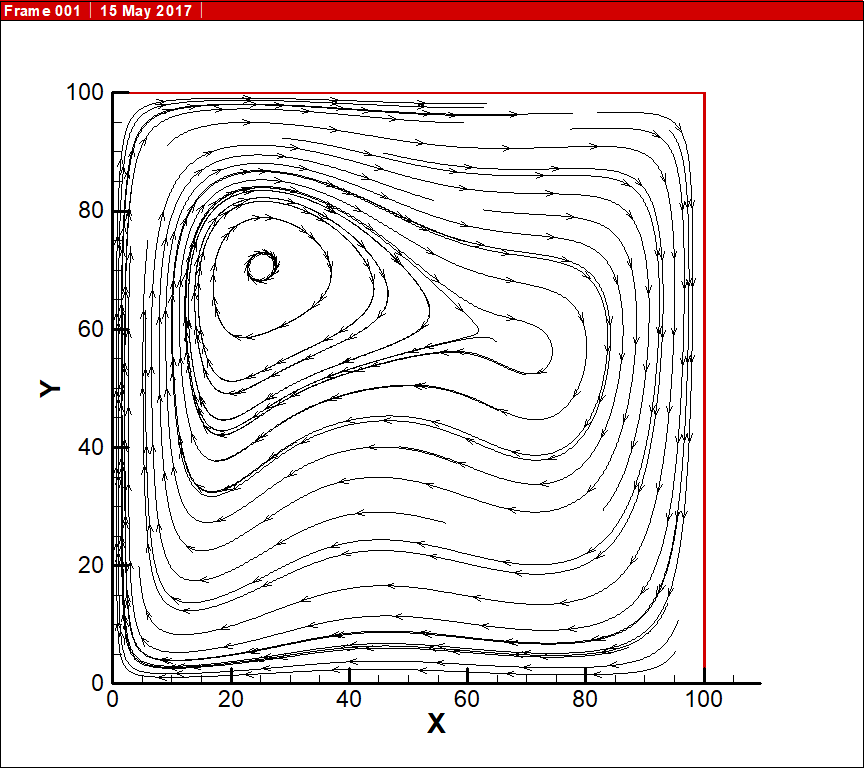
格子玻尔兹曼方法是一种介于宏观连续模拟与微观分子动力学模拟之间的介观尺寸模拟,其易于并行计算,物理背景清晰,能有效处理复杂边界条件,广泛应用于流体力学,传热学,数学,量子力学,计算机科学等诸多领域,本文使用格子Boltzmann方法D2Q9(二维和九速)模型,模拟封闭方腔自然对流,建立左壁面被加热,右壁保持常温,其他壁面为绝热的方腔模型。考虑到加热位置和瑞利数对数值模拟的影响,构建热格子TLBM模型模拟不同Ra数下自然对流,通过速度云图分布和流线图的动态变化,找出相应的自然换热规律,观察漩涡的形成,模拟结果表明:随着Ra的增大,流场的演化更为复杂,在自然对流达到稳定状态时,方腔内涡的数量越多, 左、右温壁面附近的换热越强烈,压强逐渐呈现出中心低,上、下壁面附近高的对称分布。
关键词:数值模拟 热格子Boltzmann模型 自然对流 瑞利数
ABSTRACT
The lattice Boltzmann method is mesoscopic size between macroscopic and micro simulation of molecular dynamics simulation simulation, it is easy to parallel computing, a clear physical background, can effectively deal with complex boundary conditions, widely used in fluid mechanics, heat transfer, quantum mechanics, mathematics, computer science and other fields,the lattice Boltzmann method, D2Q9 (two-dimensional and nine speed) model, is used to simulate the natural convection in a closed square cavity. The physical model of the square wall with the left wall heated, the right wall maintained at normal temperature and the other wall being insulated is established. Taking into account the heating position and the Rayleigh number of numerical simulation, construction of thermal lattice TLBM model to simulate natural convection under different Ra number, the dynamic distribution of velocity contours and streamlines, find the corresponding natural heat transfer law, observe the formation of vortex, the simulation results show that the increase of Ra, the flow field evolution is more in the complex, natural convection when reaching the steady state, the more the number of vortex cavity, left and right near the wall temperature of heat exchanger is strong, showing a low pressure center, symmetric distribution, high near the wall.
Key words: Numerical Simulationhot lattice Boltzmann model natural convection
Rayleigh number
目录
摘要 I
ABSTRACT II
第一章 绪论 1
1.1引言 1
1.2 格子-Boltzmann方法介绍 2
1.3 论文的主要研究内容 3
1.3.1研究现状 3
1.3.2 研究内容 4
第二章 TLBM模型 5
2.1 TLBM模型 5
2.2边界处理 7
2.2.1 周期格式 7
2.2.2 反弹格式 8
2.3本章小结 8
第三章 自然对流数值模拟 10
3.1物理模型的建立 10
3.2模拟结果进行分析与总结 11
3.3本章小结 14
第四章 Fluent模拟对比 15
4.1模型的建立 15
4.2 Fluent求解计算设置 15
4.3 Fluent模拟结果 16
4.4 本章小结 16
第五章 相关实验成本的经济估算 18
5.1投资估算 18
5.2资金筹措 18
5.3经济寿命期分析 19
5.4经济估算的意义 19
第六章 总结与展望 20
6.1课题的总结 20
6.2课题的展望 20
参考文献 21
致谢 24
第一章 绪论
1.1引言
本文采用的格子-Boltzmann方法是近些年得到好多领域所认可和使用的一种全新的数值模拟方法[1]。它主要吸收了格子气自动机的基本原理并对其作了深入改进。当时首先用单个流体粒子的分布函进行演化而这种方法在处理流体一些传统数值模拟时可以充分体现出它的价值,当然也可以很方便的处理复杂边界的流动问题。这种兼具微观特点的介观方法,能够从微观角度来分析组分之间的相互作用,这种方法的建立和应用具有许多优点并且简单方便,在使用的过程中会逐渐发现它具有好多优势而这些恰恰是传统模拟方法所没有的[2-3]。本文中使用的格子玻尔兹曼方法和其他的方法具有很大区别它很容易应用到各种复杂的情形中,对于传统的格子玻尔兹曼方法一般会用标准均匀网格,不过应用时要由粒子的速度空间离散格式决定,在遇到复杂边界流体流动时就不能应用,而且除了连续性介质模型所使用的网格数量较少外,其他复杂情形流体模拟时用这种方法是不适用的,所以为了解决上述问题将采用新的模型进行数值模拟。
本文中求解换热相关问题的LBM方法称为热格子方法(TLBM)[4],用于分析具有非连续效应的二维流体流动和热传递,采用以速度云图和速度流线以及不同瑞利数Ra的函数和温度轮廓来呈现传热效率的高低[5]。这里使用的TLBM采用左壁/右壁边界条件来产生强制对流,其中在壁面处的平衡分布计算被修改以包含速度和温度跳变条件进行方腔内的流体实现自然对流模拟,使用双分布函数模型,模型具有的优点一方面是稳定性好,另一方面适用范围广。本次模型同时使用速度分布函数模拟其速度的分布情况同时能看出温度对速度的影响和内能密度分布函数可以用流线图来反映其变化,由此便可以与换热分开计算,获得流场信息,通过内能密度分布函数的时间获得温度分布情况,不过在文中模拟的时候做出的结果做了改变,绘出了速度云分布图和流线分布图这种方法不仅可以改善TLBM方法的稳定性,而且可以降低黏性耗散,模型具有一定的的压缩效应[6]为了克服这种效应,本文采用一种压力和平均密度计算平衡态分布函数的方法[7]。通过这种方法可以改善速度云分布函数和内能分布函数参与粒子演化,对封闭方腔自然对流的理论和数值分析从边界层理论和量纲入手,由此建立了封闭方腔一边被升温另一边保持温度不变[8],封
闭方腔内自然对流为非稳态变化过程,在此过程中还使用了带有D2Q9(二维和九速链接)的被动标量热格子Boltzmann方法的内部计算流量求解器[9-10],研究了部分加热的方腔的自然对流特性格子模型。为了使结果更加的鲜明,引入瑞利数这一常量,通过改变Ra模拟出一系列方腔内部变化过程,在对模拟结果进行分析和总结,最终得出相应结论。
相关图片展示:
课题毕业论文、开题报告、任务书、外文翻译、程序设计、图纸设计等资料可联系客服协助查找。