摘 要

拟合优度检验是统计理论中的重要的一环，与实际应用有着密切联系,在回归分析中评价模型拟合程度的好坏是十分关键的一步。但是大部分拟合优度检验的研究都是基于一般的线性回归模型上，即含有截距的模型。而对于不含截距的模型，即过原点的回归模型，经典的拟合优度测算方法，即可决系数就可能不再适用。

首先本文将研究带截距的模型和零截距模型的性质、特点，分析两种不同回归模型的差异，根据普通最小二乘方法来分别推导在有无截距的情况下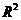的推导过程，然后探讨在有截距模型和无截距模型求解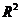的过程中出现的误差和不同之处，用蒙特卡洛方法生成随机数据，验证了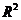存在的问题；其次，结合已有研究成果，提出三种针对过原点回归拟合优度的测算方法，分别用数据模拟，用这三种方法进行拟合优度检验；最后总结比较这三种检验方法的优劣，给出可能的进一步研究方向。

关键词：过原点模型，拟合优度检验，统计检验量。

Discussion on Method of Measuring Goodness of Fit for Cross-over-origin Regression Model

Abstract

Goodness-of-fit test is an important part of statistical theory, and has a close relationship with practical applications. It is a crucial step to evaluate the degree of fit of the model in regression analysis. However, most studies of goodness-of-fit tests are based on a general linear regression model, that is, models that contain an intercept. For the model without intercept, ie, the regression model of over-origin, the classical goodness-of-fit measure method may be no longer applicable.

Firstly, this paper will study the properties and characteristics of intercepted and zero intercept models, and analyze the differences between the two different regression models. According to the ordinary least squares method, the derivation process of R² with and without intercept is deduced, and then the errors and differences in the process of solving R² with intercept model and no intercept model are discussed. The Luo method generates random data and verifies the problem of R². Second, combined with the existing research results, three measurement methods for goodness of fit after over-origin regression are proposed. The degree of testing; the final summary of the advantages and disadvantages of the comparison of these three methods, given the possible direction of further research.

Keywords: cross-over-origin model,goodness-of-fit test,statistical test quantity

目录

摘 要 ǀ

Abstract ǁ

第一章 引言 1

1.1 研究目的及意义 1

1.2 研究相关背景 1

1.2.1 国外相关研究回顾 1

1.2.2 国内相关研究回顾 1

1.3 本文的研究方法及创新点 3

第二章 拟合优度检验的可决系数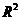 4

2.1 可决系数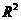的推导 4

2.1.1 有截距项模型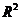的推导过程 4

2.1.2 无截距项模型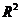的推导过程 6

2.2 有无截距项对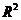产生的误差和影响 7

第三章 过原点回归拟合优度检验的测算方法比较 9

3.1 已有的过原点回归拟合优度检验测算方法 9

3.2 测算方法比较与数据分析 10

3.2.1 基于残差误差率的评价指标 12

3.2.2 基于最小二乘投影的评价指标 13

3.2.2 基于离差平方和的评价指标 14

第四章 结论与建议 15

参考文献 17

致谢 18

第一章 引言

• 1. 研究目的及意义

我们所学习研究的回归模型的拟合优度检验通常是在含常数项的模型的基础上进行的，虽然常数项在许多情况下都没有实际性的意义，但是解释变量的定义域在很多情况下并不一定包括0，但是常数项在一般回归模型里又是必不可少的。为了一个目的而去确定所有的参数，我们考虑线性回归的本质，而这个目的就是是残差项的平方和最小，并且同时要使残差项的均值为0，特别地，常数项是一个长期的、非随机的部分，不能够由自变量解释。从数学计算角度来看，残差作为对于随机扰动项的估计，需要满足无偏性质，只有这样，我们才能在进一步进行最小二乘估计，进行拟合优度检验的时候满足经典假设。所以从数据来看，有截距项的回归模型更加普适。

但是我们也知道，并不是所有的模型都一定会带有截距项的，也有可能会出现过原点回归，即无截距模型。

相关图片展示：