基于精细积分求解压力梯度作用下的平板层流边界层毕业论文
2021-03-11 23:22:07
摘 要
假如相似性解的条件得到满足,那么压力梯度作用下的平板层流边界层方程可写成一个两点边值的非线性常微分方程。精细积分法可以高精度地给出该类方程的数值解。本文介绍了边界层理论中有关平板边界层的相关理论,讨论了相似性解存在的条件,并对普朗特边界层方程进行了简化推导。随后介绍了精细积分求解的基本途径,对问题展开了编程求解,并绘出了相似性解的图像。通过对比不同压力梯度大小和方向对应的图像,探讨了压力梯度对平板边界层速度分布的影响。
关键词:平板层流边界层,精细积分法,压力梯度,有限差分法
ABSTRACT
Assuming that the solutions were similar, a plate laminar boundary layer equation under pressure gradient could be described as a nonlinear ordinary differential equation with two-point boundary value. Precise Integration Method can be applied to such equations for high-precision numerical solutions. In this paper, we introduce boundary layer theories concerning the plate boundary layer as well as discuss the prerequisite of solutions being similar, and reduce the Prandtl boundary equation. We thereafter introduce basic approaches of Precise Integration Method, coding them in order to solve the equations, and plotting the similar solutions. By comparing the figures under a variety of gradient value and direction, we thereby discuss the effect of the pressure gradient on the velocity layout.
Key words: plate laminar boundary layer; precise integration method; pressure gradient; finite difference method
一、绪论
对于黏性很小的流体(如水、空气等),在大雷诺数同平板进行相对运动时,可按流体呈现的不同特点,人为将流体划分为物面周围薄薄的一层与外部流体。物面周围的薄层称为边界层。
对于半无穷长平板的层流边界层,德国科学家布拉休斯于1908年详细讨论了其求解方法。这个问题可描述为:一个半无穷长的极薄平板迎一均匀来流,来流在平板上由于黏性作用,形成了边界层。借助平板厚度极薄的假设,我们可以引入流函数来将复杂的偏微分方程转化为常微分方程,得到如下形式的方程
(1-1) |
这是一个非线性的三阶常微分方程,虽然形式十分简单,但依然无法找出封闭形式的解来。布拉休斯当年采用级数衔接法近似地求出了近似解,而后托柏弗(Topfer)、哥斯丁(Goldstein)、豪华斯(Howarth)、哈脱利(Hartree)等人分别用数值方法求出了不同精度的解,并整理出了布拉休斯公式以供工程人员使用。
对于平板问题,布拉休斯解已经具有足够的精度。然而,很多流动问题中的壁面并非平面,这一方面是现实问题的复杂性所导致,如饱受腐蚀的水库壁面;另一方面也是人为需要,譬如机翼的表面需要一定的弯曲以达到较优的气动(水动)性能。曲面效应会导致边界层出现沿壁面的压力梯度,当壁面拓宽时是逆压,当壁面缩窄时往往是顺压。在这样的压力梯度下,原先的布拉休斯方程就无法完整描述流动现象了,必须人为加上压力梯度项,变成
(1-2) |
相比原先齐次形式的布拉休斯方程,这个方程包含了x的元素,而且也变成了非齐次方程,原本的布拉休斯解无法适用。本文对相似性解存在条件进行探讨,拟采用精细积分的方法编程计算。
精细积分法是一种近似计算常微分方程的方法,它基于泰勒展开对精确解做出近似,并对数据做出分离以避免数据储存时造成的精度损失。
精细积分法最初是钟万勰教授于1991年首次提出的矩阵指数的精细积分算法,这个方法避免了精细划分的截断误差,将矩阵指数数值解的精度提高到了计算机的程度。很快,该方法在结构动力初值问题的求解上得到了应用。在此基础上,钟万勰教授结合了计算结构力学与最优控制的模拟理论,又建立了两点边值问题的精细积分方法。
对于线性定常系统,无论是初值还是两点边值问题,精细积分方法都可给出计算机上的精确解,其精度与步长近乎无关。如今,精细积分方法已广泛应用于结构动力响应、随机振动、最优控制、热传导、波传播、偏微分方程求解、动态载荷识别、结构优化设计、刚性问题、Maxwell方程求解、复杂动力弹塑性分析等众多领域。精细积分方法与虚拟激励方法结合,成功解决了复杂结构随机振动问题的计算瓶颈;基于精细积分算法开发的LQG/Hinf最优控制系统设计与仿真工具箱(PIMCSDToolbox)也具有更高的精度和效率,现已得到哈尔滨工业大学、南京航空航天大学、国防科学技术大学等高校学者的应用,用于解决航空航天领域的快速机动控制问题。
精细积分的精度高、稳定性佳,对于两点问题有十分良好的应用,对边界层问题的求解而言是极佳的工具。
本文第二章从普朗特边界层方程讲起,引入边界层的概念,将描述黏性不可压流体的动量方程和连续性方程推导成普朗特边界层方程。在此基础上,针对平板问题引入布拉休斯方程及布拉休斯解。由于本课题考虑的是模拟曲面效应的平板层流边界层,即压力梯度作用下的平板层流边界层,所以还需人为对布拉休斯解加上压力项。此外还证明了幂次函数的速度分布必定满足相似性解条件,也就是说在这种分布下一定能将作为偏微分方程的普朗特边界层方程转化为常微分方程的形式并求解。
第三章介绍了精细积分方法计算指数矩阵式子的基本途径,推导了精细积分方法的过程公式,并估计了精细积分方法的精度。
第四章描述了应用精细积分方法求解布拉休斯方程的公式推导工作,布拉休斯方程是满足相似性解条件的压力梯度作用下的平板层流边界层方程的齐次形式,因此对于求解满足相似性解条件的压力梯度作用下的平板层流边界层方程有着重要的借鉴意义。本章从布拉休斯方程开始,通过线性化的方法将布拉休斯方程化为线性常微分方程,这意味着解可以写成指数形式。
第五章使用编程的手段对第四章的线性常微分方程进行精细积分数值求解,并同豪华斯的解进行了对比。
第六章在第五章的编程计算的基础上,对满足相似性解条件的压力梯度作用下的平板层流边界层方程进行了编程求解,绘出系列图像,在对比分析图像信息的基础上得出顺压梯度和逆压梯度下平板层流边界层的不同性质。
二、平板边界层理论
2.1 普朗特边界层方程
将连续性方程和纳维-斯托克斯方程(动量方程)联立,即可完整地描述黏性不可压流体的运动。然而其中的惯性项是非线性的,在数学上难以求得精确解,因此远不能满足工程需要。对于这类问题,一般的思路是对物理问题进行近似简化,将非线性的方程转化为线性方程,以此求得方程的近似解。这种方法的求解必须足够接近精确解,同时也要易于求解,因此我么需要对其物理本质有足够清晰的认识,对物理现象的简化也要充分考虑其主次程度。
本文要研究的物理问题是一个二维问题,描述为:一个无限长、足够薄的平板浸没于水中,相对水流体进行直线运动;此时由于黏性的影响,流场会有一定的改变,但最终会趋于一个定常的状态。本文的讨论就是以该定常状态为基础的。与此同时,人为加上水平的压力梯度,以模拟小曲度表面的曲面效应,并求解此条件下的流场速度分布。该问题的坐标系定义为:坐标原点在平板对流的一端,x轴沿原点指向平板另一端,沿原点垂直于x轴指向流场上部分为y轴,流体的速度在x、y轴上分别记为u(x,y)与v(x,y)。由于几何形状严格对称,研究第一象限的流场就可以将结论推广到整个物面影响的区域。下面的讨论都是针对第一象限流场的。坐标系的示意如图2.1所示。
图2.1 无限长平板迎均匀来流的坐标系定义示意图
无限长平板的运动在黏性的作用下会对流场产生扰动,因为水的黏度相对很小,且水的流速也非小量,加上平板的特征长度足够大,所以我们认为这个问题下的雷诺数是很大的。大的雷诺数意味着惯性力比黏性力大得多。纳维-斯托克斯方程一旦忽略了黏性项,就变成欧拉方程,这是很大的简化,我们可以用欧拉方程的结论来进行求解。然而,如果完全忽略黏性力,不仅流动无法满足物面无滑移的条件,而且也会得出达朗贝尔谬论等不符合客观物理现象的结论。因此,尽管黏性力是一个小量,但完全忽略黏性力是不妥的。
达朗贝尔谬论是达朗贝尔在1752年发表的“流体阻尼的一种新理论”一文中提出的。考虑:流体不可压缩、无黏性,物体在其中等速运动(和本文讨论的问题十分相似,只要完全忽略黏性力,本文讨论的问题就能如此描述)。可以推出物理所受的外力一定为零。由于现实中不存在无黏性流体,这种情况显然就不会发生。达朗贝尔没有对这个结论进行解释,但对于无黏性流体而言,这个结论是合理的。因此,即使流体的黏性非常小,也会对物体产生显著的影响,一旦将流体简化为无黏性流体,物理现象将会发生质的变化。
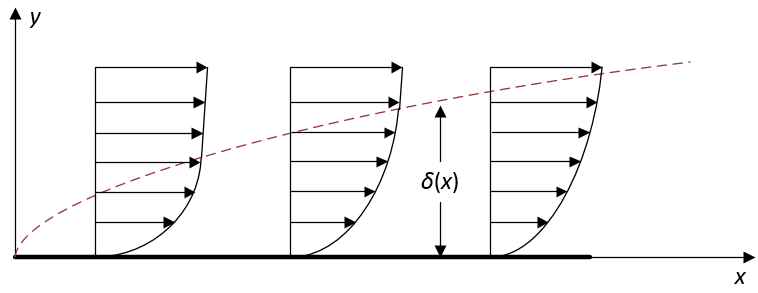
图2.2 平板附近的速度分布情况
观察平板附近的速度分布情况,如图2.2所示。整个流场可以分为两个性质很不相同的区域:一个是紧贴物面的非常薄的一层区域,称为边界层;一个是边界层以外的区域,称为外域。边界层与外域的分界线在图中用虚线标出,分界线一般规定为u等于99%U的点组成的一条线。分界线是人为规定的,代表边界层内的流体受到黏性作用足够小,或外域流体受到的黏性作用足够显著;一般不与流线重合。在外域,物面对流动的阻碍作用已经相当小,各个剖面上u的变化十分缓慢,即纵向梯度很小,因此黏性力τ=μdu/dy相对惯性力是小量。而边界层内,从物面处的u=0到分界线处的u≈U的变化要在极薄的一层内完成,纵向速度梯度可以达到很高的数值,黏性力相对显著,已经达到与惯性力同阶的程度。因此,外域忽略黏性力是可行的;而边界层的黏性力与惯性力往往同阶,不能忽略黏性力。这样,有关黏性的矛盾就得到了解决:忽略外域的黏性力而保留边界层的黏性力,不仅满足了物面无滑移的条件、规避了达朗贝尔谬论,而且也可以根据边界层极薄的特点对粘性方程做进一步的简化,不至于在整个流场内求解纳维斯托克斯方程。将黏性影响显著的近壁部分保留黏性,而对黏性影响极微弱的外域部分进行无黏处理,这就是定义边界层的基本思想。
普朗特边界层方程是在边界层极薄、边界层内黏性力与惯性力同阶的假设下,由黏性不可压缩流体的基本方程组推导而来的。这两个假设不仅符合边界层的实际物理状况,也为接下来的简化带来了便利。
首先,写出二维粘性不可压流体的基本方程组,描述边界层内的流体情况:
(2-1) |
式(2-1)中三个等式分别为连续性方程x方向动量方程y方向动量方程。方程的解满足物面和无穷远处边界条件。
记边界层厚度为δ,在边界层极薄的假设下显然δ是一个小量。又根据黏性力与惯性力同阶的假定,可以推出
对公式(2-1)中x方向的动量方程和y方向的动量方程中的各项进行估阶,并将估出的小量标灰,表示可以在方程中略去。
表2.1 动量方程的估阶 | ||||
x方向动量方程的项 | 阶 | y方向动量方程的项 | 阶 | |
其中L是假想的量纲长度,δ/L是无量纲小量。观察表格内容:y方向动量方程比x方向总体低一阶,在物理上较为次要,因此我们以如下的近似方程来替代
(2-2) |
式(2-2)表示在边界层内,压力的纵向梯度为零。外域无黏则满足伯努利方程,而给定的速度分布本身不存在纵向速度梯度,可以推出外域的纵向压力梯度也为零。因此,整个流场内可以认为
即:流场内的纵向压力梯度处处为零。
课题毕业论文、开题报告、任务书、外文翻译、程序设计、图纸设计等资料可联系客服协助查找。



