现代无线通信中信道编码技术的研究毕业论文
2020-03-28 12:18:45
摘 要
近些年来,无线通信科技的发展空前迅猛,信道编码(Channel Encoding)自诞生以来一直成为通信界的研究热点。直到现在,信道编码技术仍然是无线通信系统的一项重要技术。无线信道作为最无法把控、影响因素最多的信道,研究其信道编码将大大提高系统的可靠性,成为现代通信系统不可或缺的技术。本文将先对无线通信系统的信道编码进行研究,并针对作为第四代通信系统主流的低密度奇偶校验(Low Density Parity Check,LDPC)码进行仿真实现,分析影响系统性能的参数,并比较不同译码算法下误码率的差别,分析并得出结论。
本文对LDPC码在加性高斯白噪声(Additive White Gaussian Noise, AWGN)信道前后传输过程进行仿真,包括:LDPC码校验矩阵的构成、编码、调制、信道传输、解调、译码、误码率绘图。
关键词:信道编码;LDPC码;误码率;软判决
Abstract
In recent years, with the rapid development of wireless communication technology, Channel Encoding has been a popular research in the communication field since its birth. Until now, channel coding technology is still an important technology of wireless communication systems. As the most uncontrollable and influential channel, wireless channel research on channel coding will greatly improve the reliability of the system and become an indispensable technology for modern communication systems. This article will first research the channel coding of wireless communication systems, and simulate the realization of the LDPC code that is the mainstream of the fourth generation communication system. Analyze the parameters that affect system performance, and compare the difference in the BER under different decoding algorithms. Finally analysis and draw conclusions.
This paper simulates the transmission process of LDPC codes before and after additive white Gaussian noise (AWGN) channels, including the composition of the check matrix, coding, modulation, channel transmission, demodulation, decoding, and image of bit error rate .
Key words:Channel Coding; LDPC code; bit error rate; soft decision
目 录
第1章 绪 论 1
1.1 研究背景及意义 1
1.2 国内外研究现状 2
1.3 本文研究工作与内容安排 4
第2章 信道编码基本理论 6
2.1 卷积码 6
2.2 分组码 6
2.3 LDPC码定义及表达 7
2.4 LDPC码的编码原理 9
2.4.1 基于生成矩阵的编码算法(传统算法) 10
2.4.2 基于校验矩阵的LU算法 10
2.4.2 基于校验矩阵的RU算法 12
2.5 LDPC码的译码原理 14
2.5.1 硬判决算法 14
2.5.1 软判决算法 16
第3章 AWGN信道下LDPC码编译实现与仿真 18
3.1 校验矩阵H的构造 18
3.2 LDPC码编译码仿真 18
3.3 仿真结果分析 20
第4章 总结与展望 24
4.1 全文总结 24
4.2 未来展望 25
参考文献 26
致 谢 27
第1章 绪 论
1.1 研究背景及意义
通信最早可以追溯到远古时期,人们一开始通过一些简单的手势进行交流,到创造各种不同的语言和文字实现信息的传递。中国古代最早开始使用烽火来传达敌军来袭的消息,再到邮译传信,进而有了一骑红尘妃子笑的典故。民间传递信息的方式更是多种多样,如飞鸽传书、灯塔等。随着现代科学技术的发展,这些古老的通信方式发生了变化,应运而生航海中的旗语和现代的快递。而这些仅仅是日常生活中的通信方式,都只依靠人的视听觉,传输时间长,传输的信息容易丢失。
随着人类不断扩大交际圈,仅依赖视听觉的通信方式已经不能满足人类的需求。工业革命后,随着电话和电报的出现,通信进入一个崭新的时代——电阶段,有线通信兴起。随着电生磁现象和法拉第电磁感应的发现,电磁波开始走入人们的视线。以电磁波为传输媒介的无线通信为现代通信开辟了一个崭新的领域。通信技术随着科技迅速发展[1]。
通信的方式千千万万,但其实质就是信息的传输。在信息传输的过程中,易受到外界各种因素的影响,导致传输过程中信息丢失或者发生错误,通信系统就是来保证信息传输的高效性和有效性,所以通信系统的关键技术在于克服信道中噪声对信息的干扰,并且保证信息传输的一定效率。信息传输的效率即系统的有效性。数字通信系统具体体现在信息码占传输码的比重,即码率[2]。码率越高,系统的有效性越高。模拟通信系统体现在信号带宽上,信号带宽越大,系统有效性越差。通信系统的可靠性指的是系统信息传输的质量。模拟通信系统主要体现在输出信噪比上,信噪比是指信号与噪声的比重,信噪比越高,可靠性越好。而数字通信系统体现在误码率上,即发生错误的码数占总传输码的比重,误码率越低,其可靠性越高。通信系统的可靠性和有效性是对立的,提高有效性的同时必然会降低其可靠性[3]。设计一个通信系统,要兼顾有效性和可靠性,找到两者一个比较好的平衡点,实现信号有效且高效传输。
著名数学家克劳德·艾尔伍德·香农提出对于给定的信道容量C和信息传输速率R,若R小于C,则可以实现无差错传输,若R大于C,则无法保证任意小误码率传输[4]。这从理论上说明可以实现低于信道容量的信息传输速率可以将信息无差错传输出去。可以实现信息有效且高效传输的方式就是编码。
编码信道
图1.1 无线通信系统基本模型
如图1.1所示,为无线通信系统的一般模型[5]。信源是指产生各种各样信息的实体,是消息的来源,发出的信号为模拟信号就是模拟信源,相反发出的信号为数字信号,则为数字信源。信宿和信源刚好相反,信宿是用来接收信号的实体。信源编码器利用了压缩的原理,将连续的模拟信号通过采样变成有限个的数字信号,从而抛弃了信息中的无用部分,提高了信息的传输效率。信源译码器将信道译码器输出的信号还原为原始信号。信道编码器是将完成信源编码的信号人为地加入一定长度的监督码元,这些监督码元与信息码元有着某些对应关系。可以在信道传输后,根据这种关系可以判断信息码元的错误个数和位置,并具有一定的纠错能力,从而提高系统的可靠性。信道译码器的作用是将接收到的信息进行判错与纠错。在非理想信道传输过程中,传输的信息总是会受到一定的干扰,这种干扰称为噪声。总的来说,信源编码的目的就是为了提高系统的有效性,而信道编码的目的则是为了提高系统的可靠性[6]。因此,为了保证无线通信系统的可靠性,信道编码显得愈发重要。香农限的指出在信息传输速率不大于信道容量时,可以实现任意小误码率传输,信道编码就是实现这个理论的方法。
信道编码技术总的来说是为了解决外来的噪声对原始信息的干扰问题。通过在原始信号中加入冗余项,在接收端根据冗余项与信息之间的某种特殊关系进行判错纠错,进而降低传输的误码率,提高整个系统的可靠性。
1.2 国内外研究现状
无线通信正式被人们所重视,于上世纪七十年代开始被研究。在接下来的十年期间,以太网迅速发展,无线网以其灵活性强、不受网线框架限制等优点受到广泛认可,但由于无线网是作为以太网的一种补充,存在易受噪声干扰、传输速率低等问题,而且不同的厂商其产品也互不兼容。之后,人们把研究重点放在无线网标准上。最终于1997年,IEEE制定了802.11标准。如今,无线通信贯穿人们工作和生活的方方面面,包括WIFI、手机、数字电视等。
近几年来,无线通信领域特别是移动通信、卫星通信有了巨大的发展,信息被表示为一组二进制的码元序列在信道中进行传输。因为传输介质的缺陷和信道环境干扰,信息在传输过程中可能会发生丢失或者错误,为获得更高的传输可靠性和抗干扰能力,信道编码技术孕育而生。
信道编码技术根本目的就是为了克服来自外界的干扰与噪声导致初始信息的失真错判问题,通过信道编码技术可以提高通信系统传输的可靠性。信道编码的工作方式就是在等待发送的原始信息码段之间加入包含有一定规律的码段,这组码段称为校验信息。在接收端则利用校验信息和原始信息之间的联系发现错误甚至纠正错误。信道编码正是通过增加信息的长度来减少错误带来的影响,从而提高系统的可靠性。
1948年,香农在其论文中提出著名的信道编码定理,并阐述了信道容量的相关概念,为之后纠错编码的发展奠定了基础,出现了更为著名的信道编码定理。根据香农定理,若想在带宽已知却存在着干扰噪声的信道中无差错地传输信息,只有满足以下有两种方法:增大信噪比或者在原始信号的编码中加入纠错码。人类在信道编码领域取得的首次实质进展是在1949年,科学家R.Hamming和M.Golay正式提出了第一个实用的差错控制编码方法,这就是著名的汉明码。信道编码发展的前期,科学家们开始探究更加优秀的编码结构,努力在相对较短的信道编码得到较好的查错纠错性能。1954年,穆勒在他的“逻辑设计”一文中提出穆勒码,之后里德在他的基础上,提出了Reed-Muller码[7]。到了1955年,P.Elias最先提出卷积码这一经典信道编码方式。卷积码和分组码的不同点是它最大程度地运用了每个信息块之间的关系。1957年,循环码被普朗吉提出,随后他又在1958年提出QR码[8]。1960年,BCH码和RS码相继问世。其中,RS码又称里所码,这种信道编码方式采用的是前向纠错法。自此开始,讲究重点转向纠错编码的实用性问题。1963年,一种无限接近于香农极限的LDPC码被Robert Gallager在他的博士论文中提出,这种具有稀疏校验矩阵的分组纠错码性能优异,几乎可以在所有信道中使用。但由于硬件软件问题,一直被人们所忽视。直至二十世纪末Turbo码的提出,人们才发现Turbo码其实也是一种LDPC码。于是后来人们重新对LDPC码进行研究,成为一个新的研究热点。LDPC码目前作为第四代通信系统的主要纠错码,成为研究热点[9]。纠错编码自上世纪五十年代开始,从无到有,再到各种有效的纠错码的出现。此后纠错编码得到了迅速的发展,Goppa等学者从几何方向研究纠错码和算法,提出了维特比译码算法。
对数字通信系统而言,信道编码技术是不可或缺一步,它保证了在信号从发出到接收的全过程中数据正确可靠。随着科技的不断发展,信道编码在通信领域获得越来越广泛的应用。在深海和卫星通信领域中,RS码和卷积码级联,可以有效地纠正突发和随机错误,从而提高卫星通信质量。卷积码应用于无人机测控领域,提高指令信息的传输可靠性。在数据存储领域,高速计算机采用RS码和BCH码。在移动通讯领域,卷积码、CRC码及BCH码主要被应用于第二代移动通信,使低速数据传输和语音质量得到保证。而Turbo编码技术和卷积编码技术被广泛运用于3G系统中,无需存储,具有较好的实用性[10]。在3G传输系统中,卷积编码成为了一种高效的前向纠错码,它在CDMA系统与GSM系统中应用范围相当之广。另外,从3G开始进入了高速率数据传输业务,因此追求高效的信道编码技术显得更加急切。现在的4G通信主要采用LDPC码作为编码标准,保证高效高速的数据传输效率。
通信工程一直在寻找一种既可靠又高效的信息传输方式,这也是众多学者分析各种方式可靠性与有效性的原因。简单来讲,通信的基本就是可以将信息通过信道传输后,在接收端可以还原发送端所发送的信息。但总所周知,信道没有绝对理想的,各种人为与自然的干扰会影响接受到的信息,导致信息不能被完整地还原。因此,纠错编码就成为一门为了弥补信道中信息丢失或错误的关键技术,是现代通信系统的必要技术之一,同时也成为了研究通信方向的研究者们必须掌握的一门技术。
1.3 本文研究工作与内容安排
本文首先介绍通信的发展历程,到无线通信的出现使通信时代进入了一个全新的无线时代,再介绍无线通信系统和信道编码的诞生、纠错码的发展史,并详细描述研究的LDPC码的相关原理,最后对LDPC码编译码的实现进行仿真。
本文的主要内容如下:
第一章 由通信的发展史引出无线通信在人们日常生活中的重要地位,简单介绍无线通信系统的基本框架及各个部分的作用,提出传输信息存在错误或丢失的问题,借此引出信道编码,并简述纠错码的发展历程。
第二章 简单地介绍线性分组码的相关定理,并对LDPC码的定义、表达方式、编码算法和译码算法进行详细描述。
第三章 介绍利用MATLAB软件实现LDPC码编译码仿真,并以流程图的形式简单地说明如何构造校验矩阵、编码过程以及译码过程,最后对仿真结果进行分析,得出结论。
第四章 对LDPC码在加性高斯白噪声信道中传输前后过程的仿真,进行总结和分析,并提出仿真过程中的不足,最后做出对未来的展望。
总而言之,对LDPC码编译码的实现是对无线通信系统信道编码技术的研究,也是目前4G通信系统的研究热点之一。本次毕设的目的就是对不同译码方式下,LDPC码性能的好坏进行对比总结,并分析影响LDPC码译码性能的因素。
第2章 信道编码基本理论
在无线信道中传输的信号,必然会受到信道中各种不稳定因素的影响,从而导致信息的丢失或出错。信道编码就是以牺牲通信系统的有效性,在传输的信息码元前后加入用于检纠错的监督码元,使得在传输完成之后,对整个信息序列进行检纠错,提高整个系统的可靠性。信道编码就几乎等同于检纠错码技术,按照监督码元和原本的信息码元之间的关系可以大致分为卷积码和分组码。
2.1 卷积码
假设输入的信息码元个数为k,输出的码字个数为n,则这个n个元素的码字序列不仅仅与第一次传输的k个信息码元有关,还跟后面(m-1)次输入的k个信息码元有关。可以用(n,k,m)表示一个卷积码,这也是卷积码与分组码的最大的不同。故卷积码的编码约束度即约束矩阵数为(m 1)。卷积码需要m个储存器或者寄存器,用于存放第m次之前所有输入的k个信息码元。一般来说,k和n的大小比较小,可以选择串行输入,节省输入时长。
2.2 分组码
将信息码元以k个码元为一组,映射为含有n个码元的码组,其中信息码元为k个,监督码元为(n-k)个,监督码元起到一个检错、纠错的作用,这样一个[n,k]的码组就被称作分组码。当信息码元与监督码元存在某种线性关系时,这个分组码就被称为线性分组码。若每个信息码有q种不同的表示方式,即信息码为q进制,则整个分组码含有qk个码字。本篇论文讨论的都是二进制线性分组码,q等于2。
码元个数相同的两个码组,对应码元不同数值的总个数称为汉明距离,简称为距离。在编码过程中,任意两个码组之间的汉明距离中的最小值为最小汉明距离,最小汉明距离的大小影响分组码的检纠错能力。一个码组中所有不为零的个数叫做这个码组的码重。下面用d来表示最小汉明距离。下面为最小汉明距离与检错、纠错个数之间的关系:
(1)当需要检测出a个错误时,则要求
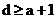 (2.1)
(2.1)
(2)当需要纠正b个错误时,则要求
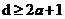 (2.2)
(2.2)
(3)当需要同时检测出a个错误,并纠正b个错误时,则要求
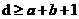 (2.3)
(2.3)
作为一个二进制线性分组码,它具有两点基本性质。第一点,码组集合中任意两个码组的模二和仍为集合中的一个码组;第二点,整个码组集合的最小汉明距离等于整个码组集合的最小码重。
线性分组码既可以由一个生成矩阵G表示,也可以由一个校验矩阵H表示[11]。
一个二进制线性分组码(n,k)的生成矩阵G由k个n维行向量组成,是一个k行n列矩阵,即:
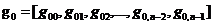 (2.4)
(2.4)
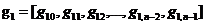 (2.5)
(2.5)
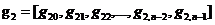 (2.6)
(2.6)
︙
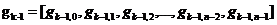 (2.7)
(2.7)
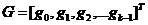 (2.8)
(2.8)
课题毕业论文、开题报告、任务书、外文翻译、程序设计、图纸设计等资料可联系客服协助查找。



