遗传算法演示系统设计与开发毕业论文
2020-03-30 12:18:04
摘 要
随着人工智能成为越来越火热的研究课题,不少智能算法及其改进应用,也越来越被人们重视。遗传算法作为其中一个较为重要且应用较广泛的算法,被更多的学者研究改进为人工智能的发展做出了很大程度的推进。
本文研究了遗传算法的主要思想,以及其各个参数对算法的影响,并运用此算法解决函数极值的求解问题和TSP问题。在解决问题的过程中,根据数据结果着重分析了遗传算法在这两个问题中的具体运用以及遗传算法的特性。在函数极值求解问题中,描述了字符串转换图像的算法和依托于QcustomPlot库开发的画图功能。在TSP问题中则给出了路径交换中城市冲突问题的解决办法。
研究结果表明:遗传算法作为一种启发式智能算法,其依托于优胜劣汰的基本思想,体现出了种群整体进化并向适应性更高的方向发展的特性,这种特性在解决某些精度要求不是特别高,但对时间要求比较高的问题上有着出色的表现,即牺牲一定的准确性来换取时间上的提高。
关键词:遗传算法;TSP问题;字符串转换图像
Abstract
With artificial intelligence becoming more and more hot research topic, many intelligent algorithms and their improved applications have been paid more and more attention. As one of the more important and widely used algorithms, genetic algorithms have been improved by more scholars and improved to a great extent for the development of artificial intelligence.
This dissertation studies the main ideas of genetic algorithm and the influence of its various parameters on the algorithm, and uses this algorithm to solve the problem of solving function extremum and TSP problem. In the process of solving the problem, the specific application of genetic algorithm in these two problems and the characteristics of genetic algorithm are emphatically analyzed based on the data results. In solving the extremum of functions, the algorithm of string converts to image and the drawing function based on QcustomPlot library are described. In the TSP problem, the solution to the urban conflict problem in path switching is given.
The research results show that the genetic algorithm, as a heuristic intelligent algorithm, relies on the basic idea of "survival of the fittest", which embodies the characteristics of the population evolution and to a higher adaptability. This characteristic is not particularly high in solving certain precision requirements, but it is excellent on the problem of high demand for time. The performance is to sacrifice certain accuracy in exchange for improvement in time.
Key Words: Genetic algorithm; TSP question; String conversion to image
目录
摘 要 I
Abstract II
第1章 绪论 1
1.1 研究背景与意义 1
1.2国内外研究现状 1
1.3本文研究内容 2
1.4本文组织结构 2
第2章 遗传算法原理分析 3
2.1 遗传算法起源 3
2.2 遗传算法发展 3
2.3遗传算法与其他算法的比较 4
第3章 遗传算法求解函数最大值及TSP问题 5
3.1遗传算法初始化方法 5
3.2遗传算法杂交,变异与优胜劣汰方法 5
3.3遗传算法中参数影响及结果分析 7
第4章 系统设计及实现 9
4.1 QcustomPlot开源库 9
4.2 字符串转换图像算法 9
4.3 求解函数最大值模块 11
4.4 求解TSP问题模块 13
第5章 总结与展望 16
5.1本文工作总结 16
5.2 未来工作总结 16
参考文献 17
致谢 18
第1章 绪论
1.1 研究背景与意义
人工智能可以说是近几年来计算机领域乃至各个领域最火热的研究方向,一门新技术的出现到成熟,会经历一条叫做“Garnet曲线”的发展轨迹,如下图1.1所示:
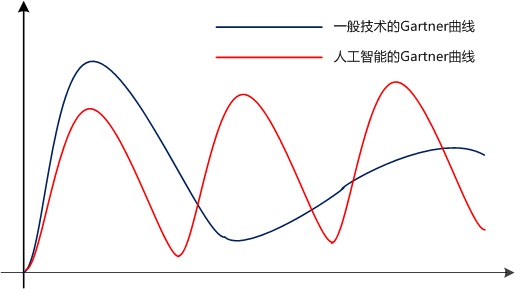
图1.1 Garnet曲线
随着大规模数据和大规模算力技术的实现,人工智能再一次回到了风口上,更多的人相信人工智能的发展会让以后的社会及工业产生重大的影响。
遗传算法实际上已经提出了很久,经历了研究热潮和冷冻期,随着人工智能的发展,这一算法也在优化人工智能模块中起到了很重要的作用,因此很多高校在培养计算机人才的时候,也会开设人工智能这样的课程,来介绍人工智能的发展和支持其发展的各个算法思想。此系统即为了能更好的展示遗传算法的过程和思想,以及用直观的图像让学习者能更好的理解并拓展。
1.2国内外研究现状
相对于最近几年兴起的人工神经网络而言,遗传算法作为一个已经较为成熟的算法思想体系,被更多的高等学校选择作为计算机学院教学知识点之一。而相对于实际运用而言,将遗传算法的演示作为中心目的而开发的演示系统较少,比较出名的是EA_demo,英国格拉斯哥大学1997年出版 ,至今仍广泛使用。
EA_demo可以让用户在网页上批次运行查看运行结果,也可以单步执行,查看遗传算法是如何运作的。用户可以改变父代数量,迭代次数,变异概率以及选择机制。
1.3本文研究内容
本系统的中心旨在提供一个可交互的界面演示系统,让人们能更直观详细的了解遗传算法的思想以及在实际问题中的具体操作流程。系统本身主要集成两个功能,即函数极限问题和TSP问题近似解的求证。
通过此系统,可以更直观的对遗传算法思想,函数极限问题求证方法,以及TSP问题近似解的求法有一定的了解。
目前传统课程教学在一定程度上已经集成了多种多媒体工具教学,但是在计算机教学领域,某些课程可以通过实际软件进行教学,但类似遗传算法这种思想教学,用编译软件,课件展示等无法很好的直观表现出来,因此一个以教学为主要目的的算法演示系统可以很好的补充这一方面的缺失,让学习之人能更好的理解并应用,同时在此思想基础上继续研究学习,从而举一反三,达到更好的效果。
1.4本文组织结构
本文共分为五章。
第一章绪论介绍全文背景意义以及国内外研究现状。
第二章集中介绍遗传算法的发展以及在现实中的运用,同时介绍一些其他类似算法进行比较分析。
第三章开始介绍具体如何用遗传算法求解函数极值和TSP问题,对遗传算法中一些重要参数的影响进行研究,并且对最终结果进行分析。
第四章主讲整个展示系统的开发与实现,以及一些界面展示说明。
第五章对全文,整个系统进行分析展望,分析优缺点以及可以改进优化的方向。
第2章 遗传算法原理分析
2.1 遗传算法起源
遗传算法作为一个算法,最早由美国密歇根大学的Holland教授为研究自然与人工系统的自适应性行为而提出的[1],其本质就要追寻到遗传这一词。而在遗传学中最出名的当属达尔文的优胜劣汰理论,遗传算法本身也是建立在此自然规律中的。为模拟出遗传的特点,在遗传算法中提出了父代编码个体,交叉概率,遗传算子,优胜劣汰等具体化过程[2]。对于每一个个体,都由一串编码来表示其蕴藏的各种抽象信息,这更像是模拟人的基因对。在每个个体的生命周期中,最重要的事便是繁衍子代,每代个体都会杂交产出后代,并且伴随着一定的变异率来防止结果收缩。产生的个体都会被评判并且比较,选出结果最差的一部分淘汰,相应的最优秀的一部分增加其个体数量来让后代得到更好的评价。
2.2 遗传算法发展
从最初简单的父代生成,杂交,变异,优胜劣汰的模拟过程为开端[3],遗传算法经历了很长一段时间的来自各个学者的优化改进,以期望得到更合适更优秀的解。
八十年代是遗传算法兴盛发展的年代,不管在理论研究上还是实践应用中,遗传算法都成了十分火热的课题[4]。1985年,在美国召开了第一届遗传算法国际会议(International Conference on Genetic Algorithms ,ICGA),并且成立国际遗传算法学会(International Society of Genetic Algorithms ,ISGA),以后每两年举行一次。1989年,Holland的学生D.E.Goldberg出版了专著 《搜索、优化和机器学习中的遗传算法》[5]。该书总结了遗传算法目前的主要研究成果,对遗传算法的理论和实际应用做出了论述。随后Koza将遗传算法与计算机编程结合起来,提出了遗传编程(Genetic Programming,简称GP)的概念[6]。在控制系统的离线设计方面遗传算法被诸多使用者证明是正确有效的策略。此后,越来越多的学术会议都将遗传算法当做是主要会议议题之一,比较著名的包括每隔一年举办一次的Parallel Problem Solving from Nature和Foundations of Genetic Algorithms[7].这些国际会议主要都讨论研究了遗传算法的理论应用和发展方向,对遗传算法起到了很好的推广促进作用。
报刊同样起到了发酵推广遗传算法的作用,越来越多的相关论文发表在了一些著名的国际报刊中,关于遗传算法的研究热潮一直在持续,越来越多不同领域的研究学者都置身于有关遗传算法的研究和应用当中[8]。
到现代社会,随着人工智能的发展,遗传算法被很多人工算法学者使用在优化过程中,这一结合把遗传算法从空间离散搜索扩展到了识别规则并生成的功能体系中[9]。这一机制为解决人工智能中优化提炼结果集起到了很好的带动作用。精炼的结果集更有利于机器的学习和优化。在另一方面,遗传算法正与其他智能算法如神经网络,混沌理论相互结合,思想的渗透有利于创造出更优秀的结果[10]。在进化规则(Evolution Programming,EP)和进化策略(Evolution Strategy,ES)等领域,遗传算法也渐渐崭露头角[11]。
2.3遗传算法与其他算法的比较
遗传算法(GA)是一种经典的启发式进化算法,其核心思想即在模拟人类自然进化的过程。人们对GA的大量研究中,提出了很多用于提高算法效率和输出结果的改进思路。算法的本质其实就是一种思想,一种解决问题的逻辑办法。不同于普通的解决逻辑,类似于遗传算法这样的算法是以宏观的角度来看待问题的,类似的算法有粒子群算法和差分进化算法等[12]。
粒子群算法(PSO)算法最早由Kenned和Eberhart于1995年提出[13]。类似于遗传算法,其初始化个体有“群体”和“进化”的过程,每一个个体可以看做是可行解空间中随机的粒子群体,每一个个体都是一个可行解,类比于遗传算法的评价判定函数,粒子群算法也有一个适应值来判定。不同于遗传算法中的优胜劣汰,粒子群会向适应值较高的方向移动,最后会形成明显的粒子群堆叠,从而得到最优可行解。
差分进化算法(DE)在 1997 年日本召开的第一届国际进化优化计算竞赛(ICEO)表现突出[14],已成为进化算法(EA)的一个重要分支,很多学者开始研究 DE 算法,并取得了大量成果。2006年 CEC 国际会议将其作为专题讨论,由此可见 DE 算法已成为学者的研究热点,具有很大的发展空间。
遗传算法,粒子群算法,差分进化算法都属于进化启发算法中的分支[15],经过长时间的积累与发展,每一个算法又多出了许多优化改进变体,针对不同的问题匹配更合适的算法。目前较为普遍的性能比较认为:这三种算法中,DE算法具有最优的性能并且具有较高的稳定性,即计算结果能很好的收敛到同一个可行解。PSO算法的收敛速度次之,但是算法收敛不一定,即稳定性上次之,最终结果容易受参数影响,但启发式算法稳定性不能作为评价一个算法是否优秀的点,启发式进化算法的本质就是牺牲最优解的保障性来获取较优解的速度,不稳定的结果集可能为最优解提供机会。GA算法的收敛速度相对较慢。
第3章 遗传算法求解函数最大值及TSP问题
3.1遗传算法初始化方法
遗传算法的第一步就是初始化父代个体,模拟个体的方法不尽相同,不同的模拟方法对算法的性能有一定的影响,因此根据实际情况进行合理的模拟是一个好的开端。
通常来说,遗传算法解决函数极限求解时,大部分使用的初始化方法是将个体转化成二进制数字,每一位都对应一个基因位,举例说明:
对于函数f(x) = sin(x),限定x的定义域为[-10,10],x的精度为0.01,此时可以将此区间看成是(10-(-10))/0.01=2000个实数组成,因为2^11=2048gt;2000,所以需要11位的二进制数来表示每一个个体。
对于一个n位的二进制数t[n],对应的整数值为t,x定义域为[x_low,x_up],精度为double则此二进制数对应的实数num有如下转换公式:
(3.1)
而对于TSP问题,就不能简单的通过二进制数来表示每一条完整的可行路径,由于TSP问题的特性,我们的每一个可行解都是一个遍布所有城市路径的全排列中的一个,因此我们可以考虑先生成一个最基础的顺序路径,即对于n个城市,此路径为[1,2,3. . .n]。然后通过随机交换多次城市位置的方式生成整个初代种群,这样即满足了TSP问题的特性。
一个好的初始化策略会对后续的杂交,变异,优胜劣汰部分起到很好的促进作用,我们在初始化个体的选择上,要尽量保证每个个体既能表达出个体特性,又能方便模拟杂交的步骤,在最后结果转换上也要尽可能简单易懂。
3.2遗传算法杂交,变异与优胜劣汰方法
个体初始化完成后,相对应的杂交变异和优胜劣汰步骤都应该简单易懂,不同的实际问题,此部分应该有不同的处理,但是每一种策略的选择都应该尽量的保证随机性,并且要避免问题过早的“收缩”,以至于陷入局部最优解使得最终结果不尽人意。对于函数极值问题,由于个体都是相同位数的二进制数,杂交方法只要将相同位置的部分交换即可得到新的个体,例如:
起始位 结束位 起始位 结束位
S1:00101101010101011 S1:00110101101010011
S2:11010101101010101 S2:11001101010101101
而对于TSP问题,不能简单的交换部分路径,这里还要解决交换了路径后会有重复路径的冲突问题,例如:
P1:1-gt;3-gt;5-gt;[8-gt;2-gt;4-gt;7]-gt;6-gt;9-gt;1
P2:1-gt;5-gt;3-gt;[2-gt;9-gt;6-gt;4]-gt;7-gt;8-gt;1
交换了路径过后:
P1:1-gt;3-gt;5-gt;[2-gt;9-gt;6-gt;4]-gt;6-gt;9-gt;1
P2:1-gt;5-gt;3-gt;[8-gt;2-gt;4-gt;7]-gt;7-gt;8-gt;1
可以看到两条路径均出现了城市重复的现象,要解决这一冲突可以用到如下算法:
对于P1路径待交换部分路径change1[n]和P2路径待交换部分路径change2[n],不相同子数分别组成一个冲突集,conflict1[m]和conflict2[m]。在P1中依次将conflict2[i]换成conflict1[i],i=1,2,. . . m。P2中同理,如此处理过后结果集将变为:
P1:1-gt;3-gt;5-gt;[2-gt;9-gt;6-gt;4]-gt;7-gt;8-gt;1
P2:1-gt;5-gt;3-gt;[8-gt;2-gt;4-gt;7]-gt;6-gt;9-gt;1
此时冲突已经得到了解决,杂交部分的路径也完整的保存了下来。
变异作为打破局部最优解的办法,其数值设置对最终结果的影响,以及结果集收敛速度有一定的影响。所谓变异,即在杂交的过程中,会有一定概率出现杂交后代出现不同于常规表现的现象,具体表现为:
在函数值求解中,某一位会由1变为0或者由0变为1。
在TSP问题中,某两个城市会交换位置。
变异的设置也应该在简单易理解的情况下,打破现有常规解,起到跳出常规,防止结果集过早收缩的情形。
每一轮杂交变异之后,将会对每一个个体进行评价,为后代选出更优秀更适合繁衍下去的后代,即优胜劣汰。对于函数极值问题,只需要将每一个个体带入到函数中求解即可,而对于TSP问题的个体,则需要计算出按此路径行走一遍的总距离来评判,最终评判后,将评价较低的个体淘汰,同时增加优秀个体,即适应性强的个体,以确保整个种群向着高评价度偏移,最终达到收缩到最优解的过程。
3.3遗传算法中参数影响及结果分析
整个遗传算法模拟了一个种群中的繁衍进化过程,在这一过程中,包含了种群数量,变异概率,迭代次数等参数。
课题毕业论文、开题报告、任务书、外文翻译、程序设计、图纸设计等资料可联系客服协助查找。



