自适应滤波器算法研究与实现毕业论文
2020-04-01 11:04:22
摘 要
自适应滤波器问世后,成为了继维纳滤波器后数字信号处理中有一个一个非常重要的组成部分。在实际应用场景中,由于缺少有用的信息来制作出固定系数的传统的数字滤波器,又或者是固定系数的滤波器无法满足信号每时每刻的改变,所以需要自适应滤波器来弥补传统的数字滤波器在功能上的空缺。自适应滤波器的功能十分之强大,能够处理绝大多数需要在未知的统计环境下的信号或着是非平稳的信号,而且其性能在通常情况下还远超于用传统的方法所设计出的固定系数的数字滤波器。除此之外,自适应滤波器还拥有着其他类型滤波器所无法达到的额外的信号处理的能力。
自适应滤波器是指利用之前时刻的结果,自动调节此刻的滤波器系数,以适应随机变化的信号和噪声的某些未知特性,来得到有效的输出信号。自适应滤波器可以去除输出信号中的噪声干扰或其他无用信息,得到与期望信号接近或完全一致的输出信号。本文首先是介绍了自适应滤波器的基本原理,其中重点阐述了自适应滤波器的两类不同的数字结构,然后再重点介绍了最小均方误差算法和递推最小二乘算法这两种自适应滤波算法,并进一步对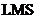 算法和
算法和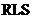 算法性能进行了细致的对比。发现
算法性能进行了细致的对比。发现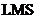 算法不仅具有结构简单,而且鲁棒性强的特点,虽其收敛速度很慢,但是相比于收敛速度更快的
算法不仅具有结构简单,而且鲁棒性强的特点,虽其收敛速度很慢,但是相比于收敛速度更快的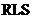 而言,其计算复杂度较小。最后本文对基干
而言,其计算复杂度较小。最后本文对基干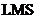 算法及
算法及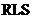 算法的自适应滤波器各自进行了相应MATLAB仿真。而实验结果也进一步的验证了上述观点的正确性,虽
算法的自适应滤波器各自进行了相应MATLAB仿真。而实验结果也进一步的验证了上述观点的正确性,虽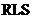 算法的收敛速率比
算法的收敛速率比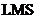 算法快,但稳定性也随之相对较低。
算法快,但稳定性也随之相对较低。
关键字: 自适应滤波 LMS RLS FIR结构滤波器
Abstract
Adaptive filter is an critical part of digital signal processing. In practical applications, we always need to design an adaptive filter for the reason that there is not enough information to design a fixed coefficient digital filter, or the fixed coefficient will change when the filter is running normally. An adaptive filter can provide an effective solution to any signal that needs to be processed in an unknown statistical environment or when a non-stationary signal needs to be processed, and its performance is usually far more than a fixed coefficient filter designed by a conventional method. In addition, adaptive filter can also provide additional signal processing capability that non adaptive methods can not provide.
Adaptive filters use the results of the previous time to automatically adjust the current filter coefficients to adapt to the unknown characteristics of random changes of signals and noise, and to obtain effective output. Adaptive filter can remove noise or useless information in output signal, and obtain small distortion or no distorted output signal. This paper first introduces the theoretical basis of adaptive filter, focuses on two different digital structures of adaptive filter, and then concentrates on the two different adaptive filtering algorithms, the least mean square error algorithm and the recursive least square algorithm, and then compares the performances of the LMS algorithm with the RLS algorithm. LMS algorithm is not only simple in structure but also robust, and on the other hand, its convergence speed is very slow, but compared with RLS with fast convergence speed, its computation is very small. Last, the simulation of the adaptive filter of the backbone between LMS algorithm and the RLS algorithm is carried out on MATLAB respectively. The experimental results show that adaptive filtering plays an important role in adaptive signal processing, and adaptive filter is widely applied in many fields. RLS algorithm converges faster than LMS algorithm by an order of magnitude, but its stability is relatively reduced.
Key words: adaptive filter; LMS algorithm; RLS algorithm; FIR filters
目录
第一章 绪论 1
1.1研究背景及意义 1
1.2国内外发展现状 1
1.3本论文主要研究内容及结构安排 2
第二章 自适应滤波器原理综述 4
2.1自适应滤波器的基本理论 4
2.2自适应滤波器的基本结构 6
2.2.1自适应横向滤波器 6
2.2.2自适应格型滤波器 7
2.3 本章小结 8
第三章 自适应滤波算法 9
3.1 最小均方误差(LMS)算法 9
3.2 最小均方差(LMS)算法的性能分析 13
3.3递归最小二乘(RLS)算法 14
3.4递归最小二乘(RLS)算法的性能分析 17
3.5自适应算法的分析比较 18
3.6 本章小结 18
第四章 基于Matlab的自适应滤波器仿真 19
4.1基于LMS算法的自适应滤波器仿真与分析 19
4.2基于RLS算法的自适应滤波器仿真与分析 21
4.3本章小结 22
第五章 总结与展望 23
5.1 总结 23
5.2 展望 23
参考文献 24
附录 25
致谢 28
第一章 绪论
1.1研究背景及意义
滤波器这一术语常常用来称呼一个系统,而设计这样一个系统是为了从含有噪声的数据中提取到所期望的,并且符合规定的信息。滤波器可以分为两种,即线性滤波器和非线性滤波器。若滤波器输出端滤波的量与它的输入端输入用于测量的信号为线性关系,这种情况下我们就认为该滤波器是线性的;否则我们就认为该滤波器是非线性的。
在解线性滤波器问题的统计方法中,通常假设有用信号及其附加噪声的某些统计参数(例如,均值和自相关函数)已知,需要设计含噪声数据作为作为其输入的线性滤波器,使得根据某种统计准则噪声对滤波器影响最小。对于平稳输入,其解决方案所采用的滤波器通常称为维纳滤波器。可是当输入端的信号或噪声是非平稳的时候维纳滤波器却难以得到令人满意的滤波效果。于是在这种情况下,我们可以设想最优滤波器为时变形式,来进一步采取卡尔曼滤波器。包括维纳滤波器和卡尔曼滤波器的线性滤波器理论已经得到广泛的研究。然而,线性维纳滤波器的设计必要使用所要处理的数据在统计方面的某些先验知识,并且只有当输入滤波器的信号的某个统计特性与滤波器设计时所依赖的这一先验知识互相匹配时,滤波器的输出才是最优的滤波结果。而当这个信息并不确定或者完全未知时,该设计就不是最优的。为消除这一限制,可采用自适应滤波器。
能够在使用前一时刻获得滤波结果,自动地调整当前时刻的滤波系数,从而达到最优滤波的滤波器,我们把能实现这种功能的滤波器称之为自适应滤波器。自适应滤波器常常具有较好的自学习与自跟踪能力,能够对各类不同的随机信号进行可靠地检测与准确地估计。设计出恰当的自适应算法来驱动采用了适当的数字结构的自适应处理器是设计自适应滤波器所需要考虑的基本步骤。其中,最关键的也是人们长期以来的研究热点是自适应滤波算法,可以简单的划分为线性自适应算法和非线性自适应算法,非线性自适应算法往往具有相较而言更强的信号处理与分析能力,但是它的计算却更为复杂,故实际场景中应用的更多的依然是线性自适应滤波算法[1]。
1.2国内外发展现状
早在上世纪的40年代,人们就对平稳的随机信号建立了世人皆知的维纳滤波理论。这种滤波器能够严格的按照干扰噪声以及有用信号某些方面的统计特性这一标准,以线性最小均方误差达到最小来得到最佳滤波效果。可是当我们无法得知输入信号在某些方面的统计特性时,滤波效果就无法达到最佳甚至表现的很糟糕。在20年之后,随着空间技术的蓬勃发展,又产生了闻名于世卡尔曼滤波理论,这种滤波器利用了状态变量模型,不仅能对能够对非平稳的序列,而且当面对多输入多输出等多种随机序列时,也能作出最优滤波。卡尔曼滤波器在面对非平稳的随机信号时,既可以按照要求进行有效地线性最佳滤波,同时针对不同需要进行非线性滤波[2]。
然而只有在对信号和噪声的统计特性进行了初步了解的情况下,这两种滤波器才能获得满意的滤波效果(最优解)。在1967年,Widrow B又根据实际的需要进一步的提出了自适应滤波理论,该理论可使在事先不知道有关输入信号和噪声的某些统计特性知识的条件下,设计出能达到最优滤波结果的滤波器,它是通过在自己的滤波过程中逐渐估计出所需的统计特性,并以此为依据自动调整自己的参数,最后在用于收敛的时间充足的条件达到最佳的滤波效果。而当输入信号的统计特性发生改变时(实际情况往往如此),它又能够察觉到这种变化,自动调整系数,使滤波器性能又达到最佳。
虽然我们可以通过各类不同的算法来实现自适应滤波器的自动调节系数,但是由于它采用的是一种逼近的算法,这种算法导致了实际的计算值和期望的理论值之间必然存在一定的差距,这也就造成了自适应滤波问题可能产生多个解。现在较为广泛使用的自适应滤波方法主要还是基于下面的几种基本理论,再结合递推算法推导出来的:
(1)基于维纳滤波理论的方法: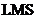 算法;
算法;
(2)基于最小二乘准则的方法:自适应递归最小二乘法(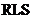 );
);
(3)基于卡尔曼滤波理论的方法;
(4)基于神经网络理论的方法。
虽然基于后面两种基本理论的方法在收敛速率以及稳定性方面能有着更好的性能,但是,第一种基于维纳滤波理论的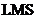 算法和第二种基于最小二乘准则的
算法和第二种基于最小二乘准则的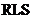 算法有着更加简单的算法,而且也能达到令人满意的滤波效果,成为了更为应用广泛的自适应算法。
算法有着更加简单的算法,而且也能达到令人满意的滤波效果,成为了更为应用广泛的自适应算法。
1.3本论文主要研究内容及结构安排
本文的主要研究思路如下:
第一章:先给出自适应滤波器的研究背景及意义,接着讲述了自适应滤波器的各类应用,然后深入探讨了国内外研究发展现状与前景。
第二章:采取逐步深入的方法,首次讲自适应滤波器的原理,再介绍自适应滤波器的结构及其重要性,最后重点介绍自适应滤波器的横向结构。
第三章:在第一章和第二章的基础上,先详细地讲述了两种常使用的自适应滤波的算法,即最小均方误差(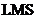 )算法和递推最小二乘(
)算法和递推最小二乘(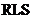 )算法,接着再针对这两种算法的各类性能指标进行了分析与对比。
)算法,接着再针对这两种算法的各类性能指标进行了分析与对比。
第四章:首先基于第三章讲述的两种基本算法的自适应滤波器在MATLAB平台上进行的仿真实验,接着进一步通过仿真实验结果分析出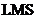 算法和
算法和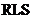 算法各有自己的优缺点,它们各有自己适合使用的场景。
算法各有自己的优缺点,它们各有自己适合使用的场景。
第五章:在前四章理论与实验的基础上,进一步分析了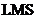 算法和
算法和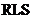 算法的优缺点,并进行归纳总结,并对后续工作进行展望
算法的优缺点,并进行归纳总结,并对后续工作进行展望
本文的主要工作如下:
(1)首先根据选定毕设题目,查阅了关于自适应滤波方面的各类中英文文献,并认真学习了自适应滤波器的基本设计原理;
(2)接着再查阅了有关将自适应滤波器设计应用于MATLAB平台上这一方面的参考资料;
(3)然后通过对毕设要求中(也是实际中两种最常见的)自适应滤波的算法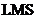 算法和
算法和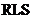 算法的进行了深入研究,了解了它们各自的优缺点以及各自的适用场合;
算法的进行了深入研究,了解了它们各自的优缺点以及各自的适用场合;
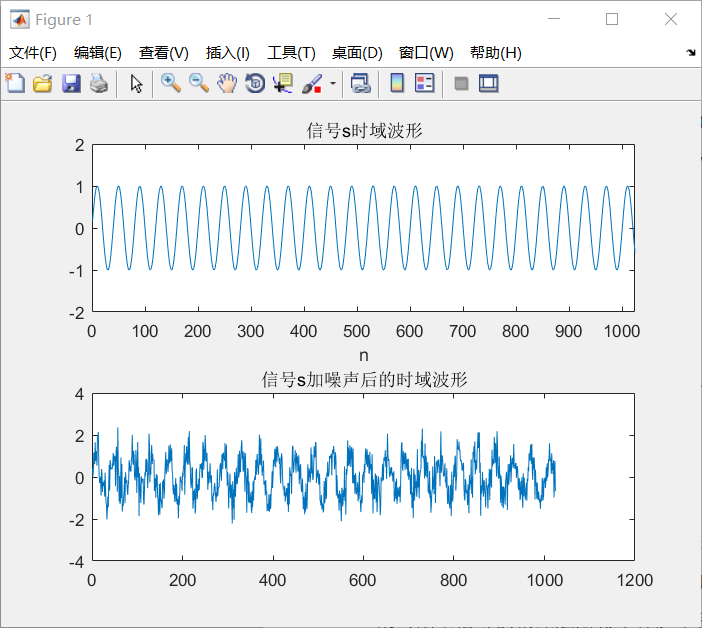
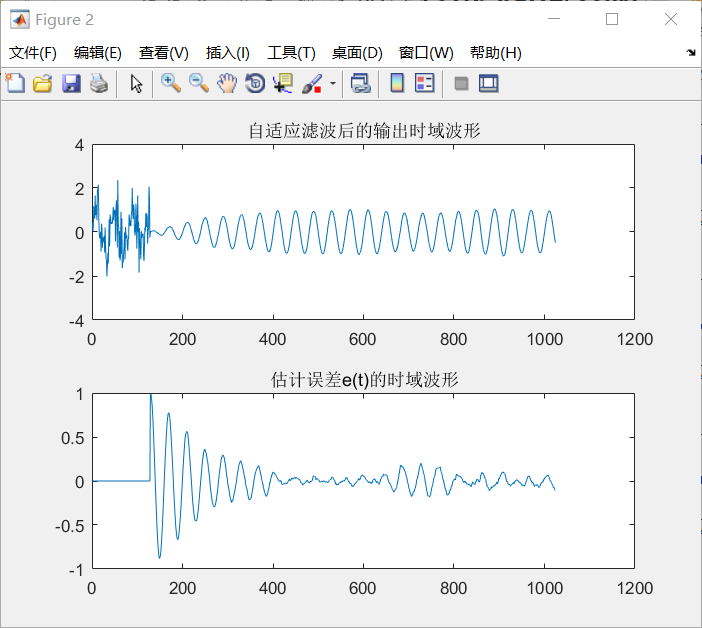
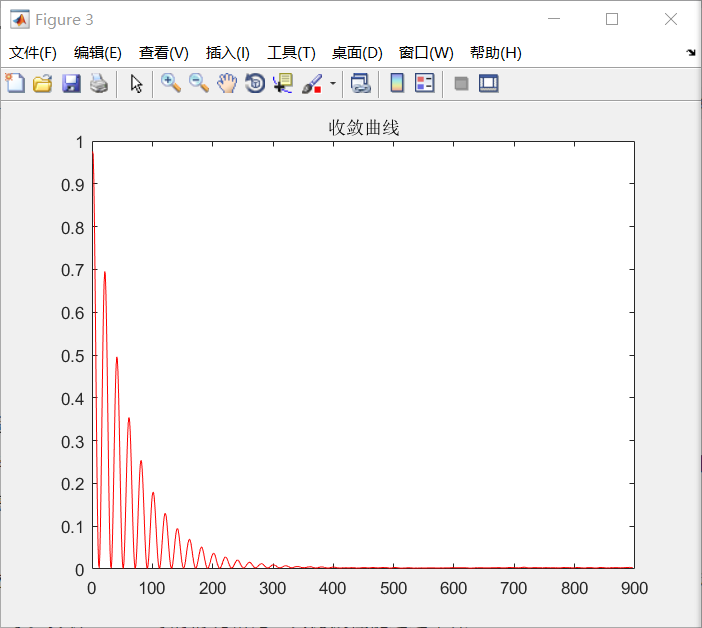
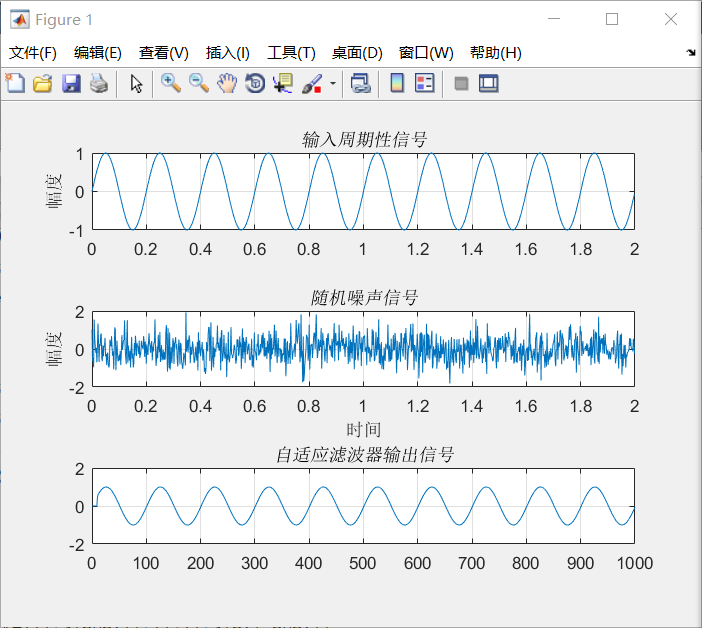
(4)最后对基于上述的两种自适应算法的自适应滤波器进行了仿真实验,通过实验进一步验证之前提出的原理。
自适应滤波器原理综述
-*//*-所谓自适应滤波,就是使用之前时刻已获得的滤波器系数等结果,自动地改变当前时刻的滤波器系数,通过这种方式来实现适应信号和噪声统计特性未知的,又或者随着时间变化的功能的滤波手段称为自适应滤波,自适应滤波通常能得到令人满意的最优滤波结果。所谓“最优”是需要选取一定的准则来度量的,在实际场景中使用最多的准则也就是即将介绍的最小均方误差准则以及最小二乘准则。
自适应滤波器可以通过改变自身的系数来达到最佳滤波的效果。自适应滤波及基本过程常常可以划分为:“学习过程”和“跟踪过程”,其中学习过程常常是指依照输入的统计特性未知信号,来改变自身的系数从而使滤波效果能到最佳的过程,而跟踪过程是指若在输入信号统计特性发生变化时,滤波器及时的调整自身的系数来达到最佳滤波效果的过程,这也就是自适应滤波器能够具有较好的学习和跟踪的性能的原因[3]。调整系数的是为了接近、达到或保持最优滤波,也就是滤波器输出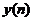 中的噪声干扰在某种准则下达到最小。
中的噪声干扰在某种准则下达到最小。
自适应滤波器可以从很多不同的方面进行分类,按其滤波器所采用的数字结构可以划分为开环和闭环两类自适应滤波器;按自适应处理器的类型可以分为递归型和非递归型,也即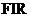 和
和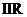 ;按其自适应算法更是可以划分为
;按其自适应算法更是可以划分为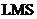 自适应滤波器、
自适应滤波器、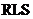 自适应滤波器等多种滤波器。
自适应滤波器等多种滤波器。
根据复杂度这一准则来分,可划分为线性的自适应滤波器以及非线性的自适应滤波器,后者虽然具有更为强大的信号的处理和分析能力,但是由于后者的计算相较而言更加复杂,硬件上的实现相较而言也更加困难;而前者及其所相应的算法具有结构较为容易、计算复杂度也较低的优势,在分析和实现方面也很容易,被广泛应用于实际的自适应信号处理系统之中;在线性自适应滤波器的实际应用中的常见情况:当自适应滤波器的学习过程结束的时候,滤波器系数就不会再变化,此时滤波器就转化为线性系统,故这种自适应滤波器在实际中也被称为线性自适应滤波器,而线性自适应滤波器因为便于设计且易于进行数据处理,所以实际仍然是使用率最该的自适应滤波器。
线性自适应滤波器的数字结构既可以采用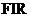 型结构,也可以是
型结构,也可以是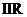 型结构。对比于采用
型结构。对比于采用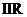 型结构的自适应滤波器,由于采用
型结构的自适应滤波器,由于采用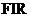 结构的自适应滤波器的自适应技术在实现方面更加简单,且其权系数的更改,也就是滤波器性能的调整也更加容易,同时因为采用
结构的自适应滤波器的自适应技术在实现方面更加简单,且其权系数的更改,也就是滤波器性能的调整也更加容易,同时因为采用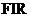 结构的滤波器是绝对稳定的,其极点永远在单位圆内,具有更加优秀的鲁棒性,所以
结构的滤波器是绝对稳定的,其极点永远在单位圆内,具有更加优秀的鲁棒性,所以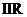 结构的滤波器虽然能够以更小的计算复杂度来实现和
结构的滤波器虽然能够以更小的计算复杂度来实现和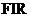 滤波器相同的功能,但
滤波器相同的功能,但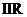 型滤波器在自适应处理过程中,会使滤波器产生输出信号不稳定的现象,再者由于通常一个稳定的
型滤波器在自适应处理过程中,会使滤波器产生输出信号不稳定的现象,再者由于通常一个稳定的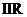 滤波器总是可以用一个采用足够多阶的
滤波器总是可以用一个采用足够多阶的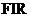 结构的自适应滤波器来近似的替代,于是我们在实际工程中一般都会采用
结构的自适应滤波器来近似的替代,于是我们在实际工程中一般都会采用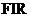 型结构的自适应滤波器,材用
型结构的自适应滤波器,材用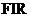 型结构作为自适应滤波器的结构也具有更加广泛的应用场景。
型结构作为自适应滤波器的结构也具有更加广泛的应用场景。
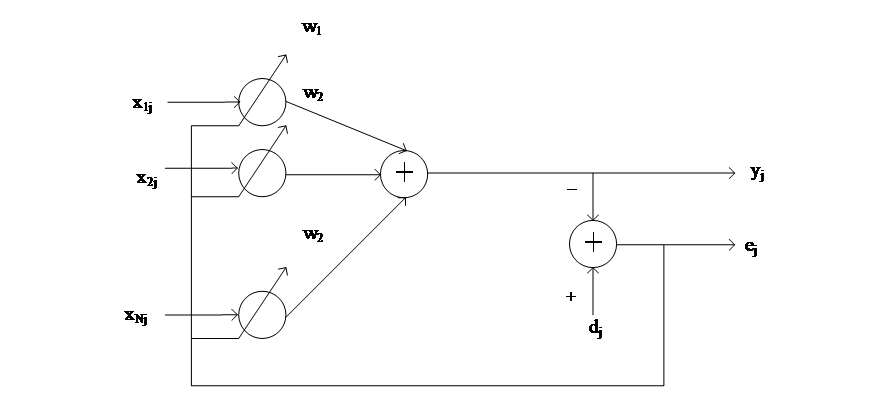
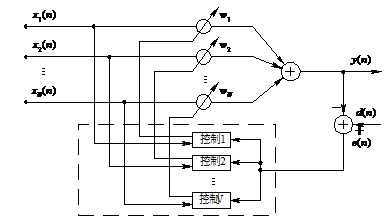
自适应算法通过调整可编程滤波器的系数来使自适应滤波器的特性发生变化。图2.1给出了自适应滤波器的一般结构,在输入信号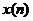 (常带有噪声干扰)通过可编程的滤波器后产生了响应
(常带有噪声干扰)通过可编程的滤波器后产生了响应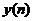 (实际所获得的输出信号),接着将其与参考信号
(实际所获得的输出信号),接着将其与参考信号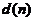 (这就是我们所期望的信号)进行对比,得到的误差
(这就是我们所期望的信号)进行对比,得到的误差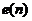 (用于性能参考),并以此通过某些自适应算法对滤波器系数进行改变,最终使得误差
(用于性能参考),并以此通过某些自适应算法对滤波器系数进行改变,最终使得误差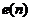 的均方值缩减到最小。
的均方值缩减到最小。
以上是毕业论文大纲或资料介绍,该课题完整毕业论文、开题报告、任务书、程序设计、图纸设计等资料请添加微信获取,微信号:bysjorg。
相关图片展示:
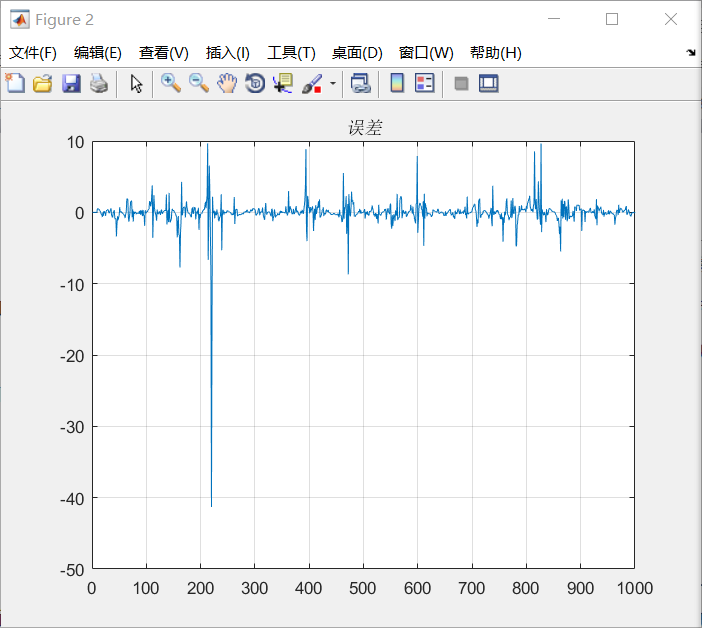
课题毕业论文、开题报告、任务书、外文翻译、程序设计、图纸设计等资料可联系客服协助查找。



