数值模型选择对定容燃烧弹内甲醇燃烧模拟的影响毕业论文
2020-04-05 10:57:49
摘 要
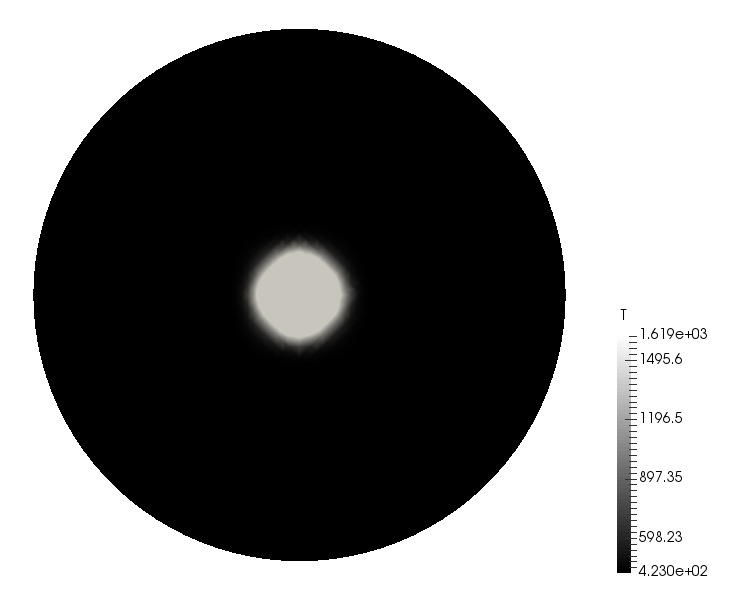
甲醇类作为代用燃料具有广阔的发展前景,得到了相关燃烧学研究的重视。采用定容燃烧弹研究甲醇向外传播层流火焰是一种很好的方式。并且数值模拟是甲醇燃烧实验的重要补充。本课题基于OpenFOAM计算流体力学软件框架,在定容燃烧弹模型中研究甲醇向外传播球形火焰的数值模拟结果与燃烧机理、初始条件等的影响。数值模拟得到了较好的结果,火焰成像较好。根据模拟数据计算了最高燃烧压力、最高燃烧温度等数据与实验结果进行比较。并结合实验数据,在不同条件下对比了详细机理与一种简化机理的准确度,得出了简化机理在中低当量比和低温低压条件下表现较好的结论。同时也对比了模拟结果与实验数据的不同,分析了误差出现的原因,并提出了若干改进模拟结果准确度的方法。
关键字:数值模拟;OpenFOAM;定容燃烧弹;燃烧机理;球形传播火焰
Abstract
As a substitute fuel Methanol has a broad prospects of development, and has received attention from related combustion studies.It’s a good way to study the Methanol outward propagation sphere flame using constant volume bomb model. And numerical simulation is an important supplement to the methanol combustion experiment.This research is based on the OpenFOAM CFD framework,studies the effects of combustion mechanisms, numerical schemes, and boundary conditions on the results of outward propagation sphere flame numerical simulation in a constant volume bomb model. Numerical simulations gave good results and the flame imaging was good. According to the simulation data, the maximum combustion pressure and the maximum combustion temperature were calculated and compared with the experimental results. Combined with experimental data, the accuracy of a detailed and a simplified combustion mechanism under different conditions was compared. It is concluded that the simplified mechanism performs better under medium and low equivalence ratios and low temperature/pressure conditions. At the same time, it also contrasted the difference between simulation results and experimental data, analyzed the causes of the errors, and a method to improve the accuracy of simulation results was proposed.
Key Words:numerical simulation;OpenFOAM;constant volume bomb;combustion mechanisms;outward propagation sphere flame
第1章 绪论
1.1引言
近些年来,代用燃料相关研究一直是燃烧学的重要开展方向。紧迫的能源形势、日益严格的排放法规以及不断提高的环保意识,都是推动代用燃料研究与应用的巨大动力。常用的代用燃料有天然气(CNG)、液化石油气(LPG)、二甲醚(DME)、生物柴油、醇类燃料等。其中,甲醇(CH3OH),是结构最简单的醇类燃料,具有成本低资源丰富、热效率高等优势。甲醇汽油、甲醇柴油由于对发动机改动小、排放性能优异,已经得到广泛运用。国家标准化管理委员会在2009年批准颁布了《车用甲醇汽油》国家标准[1],这推动了一大批甲醇燃料相关的研究,国内迎来了甲醇燃料的应用与发展契机。
甲醇的燃烧机理相对简单,易于研究。开展甲醇燃烧相关的研究对更复杂的醇类燃料、含氧燃料研究具有重要启示作用。目前,针对甲醇燃烧的研究主要从三个大的方向展开:
(1)第一个方向是关于甲醇燃烧的实验研究,这是研究甲醇燃烧最经典而有效的方法。模拟实验装置通常可分为高速循环机、定容燃烧弹、高速压缩机等,其中定容燃烧弹由于其简单的结构、易于改变的初始条件,得到了十分广泛的应用。燃烧实验主要采用原位光谱诊断法和取样分析法来研究化学反应动力学机理[2]。
(2)第二个方向是关于甲醇燃烧理论模型的建立,包括建立详细的甲醇反应路径、建立火焰速度与初始温度、压力、当量比的经验公式等。理论模型研究是实验研究的重要补充,有利于深入探究化学动力学机理。理论模型普遍存在的问题是,特定的模型在其适应的初始条件下精度较高,而超出这一范围则精度变差。目前有许多研究提出新的理论模型或改进现有模型的方法。
(3)第三个方向是关于甲醇燃烧的数值模拟,通过建立良好的模型,数值模拟方法能够得到十分接近于模拟实验的结果。相比于实验的方法,数值模拟具有成本低、操作时间短、易于改变初始条件的优点,因此得到广泛的应用。而数值模拟存在网格划分、模型选择等问题,处理不当容易导致模拟结果偏离实验结果。
其中,预混层流燃烧一直是研究的热点。层流燃烧是湍流燃烧的基础,而与湍流燃烧相比,层流燃烧实验简单可靠,测量结果准确。测定层流燃烧速度,可以作为湍流燃烧模型的基本输入数据,同时提供了验证化学反应动力学机理(下文简称燃烧机理)有效性的重要方法[3]。现有研究利用定容燃烧弹装置,通过实验系统地研究了甲醇-空气混合气体的燃烧特性[4][5]。另外一些文章提出适用于甲醇-空气预混燃烧的详细或简化机理,并初步验证了其吻合性[6][7][8]。而系统地研究甲醇-空气混合气体数值模拟的课题并不多。数值模拟是研究燃烧机理的必要手段,探究数值模拟中燃烧机理和初始条件对模拟结果的影响有十分重要的意义,本课题也将围绕此内容展开。
1.2目标与内容
对于燃烧数值模拟,学术上常采用Fluent、CFX和COMSOL等商用CFD软件,不同的是,本课题将选用OpenFAOM软件框架进行数值模拟。与商用CFD软件最大的不同是OpenFOAM完全开源,采用OpenFOAM不仅能够节约成本,还由于其开源的特性,十分便于定制修改程序以满足计算需求。因此,本课题将围绕采用OpenFOAM建立定容燃烧弹模型模拟甲醇-空气预混燃烧的整个过程展开,主要包括以下方面内容:
(1)控制方程建立、燃烧机理选择;
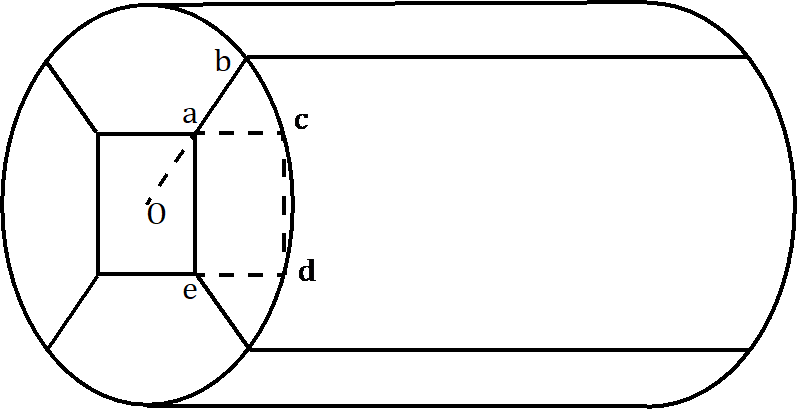
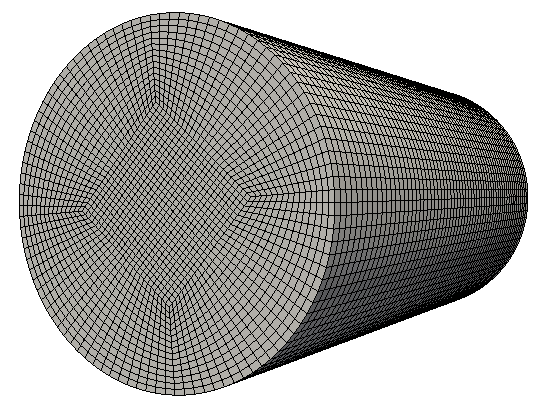
(2)定容燃烧弹的模型建立、网格划分;
(3)边界条件、离散格式、代数方程求解器等求解设置;
(4)选择不同燃烧机理、初始条件进行模拟计算;
(5)数据后处理与燃烧特征计算;
(6)实验结果与模拟结果的对比分析。
第2章 数学模型
燃烧过程分为许多种类型,在本课题中模拟的是气态预混层流燃烧,即涉及化学反应的燃料与氧化剂均为气态,并且在点燃之前预先混合,流动状态为层流。下文所述的燃烧均指气态预混层流燃烧。
燃烧是一个十分复杂的过程,需要考虑热力学、化学平衡、化学动力学等问题[9]。在一定温度条件下,不可压缩流体的速度和压力可以由连续性方程和动量方程求出,而涉及化学反应的流体要额外考虑能量传输、组分变化等。
通过计算流体力学(CFD)解决燃烧问题的核心是采用计算机求解控制流体的偏微分方程组(Partial Differential Equations,简称PDEs)。在OpenFOAM框架下偏微分方程组通过求解器(solver)得到表达,采用编程的方式在求解器中写入偏微分方程后,经过离散化和代数方程求解器的求解,最终解决问题。
在OpenFOAM中常采用涉及化学反应的reactingFoam求解器解决燃烧问题,其偏微分方程包括:
2.1 连续性、动量、能量方程
连续性方程是质量守恒定律在流体力学问题中的表述形式,动量方程是动量守恒定律(牛顿第二定律)在流体力学中的表述,能量方程则来源于能量守恒定律。CFD中最基础的假设是采用连续介质流体模型,即速度密度都连续、可微。
燃烧反应中的流体局部密度不定,其依赖于温度、压力、组分浓度。由于流体性质受到温度的影响,连续性、动量方程与能量方程相关联。连续性方程、动量方程和能量方程又被称为流体力学三大基础方程。
2.1.1质量、动量方程
质量守恒:
(2.1)
动量守恒:
(2.2)
其中:
- 混合气密度,定义为:
(2.3)
( - 混合气平均摩尔质量,
- 气体常数 ,
- 温度,
- 压力)
- 时间,
- 速度,
- 动量通量,在牛顿流体中定义为:
(2.4)
(:混合气动力粘度,
:单位矩阵)
- 重力。
在上述方程中,物理量都采用了张量标记法(tensor notation)。在OpenFOAM中表述偏微分方程时,除标量以外的物理量都习惯性地采用张量标记法,将一个物理量视为一个整体,而不是各组成分量,这样就可以使方程简单明了,便于在OpenFoam中通过编程表述出来。与此相对的是序数标记法,例如上述质量守恒方程在许多文献中常表述为:
(2.5)
相比张量标记法就显得不够简练。
另外一个更重要的原因是,采用张量标记法代表物理量不随参考系发生变化。由于线性空间的对称性,同一个物理量可以由不同的矩阵表示出来。例如上式中的,如进行坐标变换后变成,这三个值发生改变,但仍表示同一个物理量。这种依赖于坐标系的特点,不利于物理定律的表述。总的来说,使用张量标记法表述的方程保证了物理定律不随参考系变化这一性质,从记号的角度来讲也更为简洁。本章节中的方程都一律采用张量标记法。
2.1.2能量方程
燃烧过程中施放的能量通常有两类表示方法,一种是内能,一种是焓。这两种形式都可以在能量方程中采用,本质上是等价的,都是系统内能量守恒定律的表述。不同类型的流体和流动类型按照习惯会采用不同的能量形式。例如求解液体问题常采用内能,而涉及气体的问题尤其是燃烧问题更倾向于使用焓。[10]
OpenFOAM中,常引入比能(specific energy),表示单位质量的总能量,由三部分构成:单位质量动能(kinetic energy)、内能(internal energy)以及重力势能(gravitational potential energy)。从微观角度看,微元能量变化有三个来源:自身的能量产出或消失、流入或流出的能量、做功增加或减少的能量。总能量方程为:
(2.6)
其中:
- 单位质量的动能,,
- 单位质量的内能,则微元比能,
- 比热源,表示单位时间、质量的能量产出,
- 热通量矢量,
- 剪切力。
在燃烧问题中,常将总能量方程改写为焓方程,定义比焓:
改写为:
(2.7)
在reactingFoam求解器中忽略了和两项,并假设,则方程最终简化为
(2.8)
2.2组分输运方程
在燃烧化学反应过程中,化学组分间发生反应建立产物,并且吸收或释放热量,在这个过程中,新的化学组分和热量变化会随着流动而传递。这个过程中的能量和化学组分平衡方程叫做组分输运方程(species transport equations),简称组分方程或输运方程。此方程是燃烧建模的基础,假设化学组分的质量分数为、...,则组分输运方程可表述为:
(2.9)
()
扩散项中表示组分的扩散系数。产生扩散项的分子输运过程十分复杂,在reactingFoam求解器中仅采用最基础的二元通量近似值来计算扩散项。在湍流输运过程比分子输运过程重要的情况下二元通量近似值较为准确[11]。
源项代表组分的产出或消耗,与化学反应机理相关联。假设组分的净反应速率为 ,则源项:(为摩尔质量)。在每次求解迭代中,为了通过组分输运方程得到各组分的质量分数,必须先求出源项,这就需要求解大量与化学反应相关的常微分方程。化学反应机理越复杂,计算规模就越大。源项的计算量占了燃烧数值模拟中的绝大部分,为了优化性能,就要求在保证燃烧机理准确性的前提下简化燃烧机理,这将在后续章节中讨论。
reactingFoam求解器的源代码中有数个代表方程的头文件:
头文件 | 代表方程 |
EEqn.H | 能量方程 |
pEqn.H | 状态方程 |
UEqn.H | 动量方程 |
YEqn.H | 组分方程 |
表2.1 头文件
写入或修改头文件中的方程,再经过编译,可以生成求解器,通过运行求解器即可求解方程。
偏微分方程的编程表示是OpenFOAM的一大特点,其语法十分接近数学表达式,十分简洁而有条理。虽然其基于C 语言,但通过OpenFOAM类的继承,不需要太多C 知识就可以将方程表示出来。例如UEqn.H中的动量方程表示为:
fvVectorMatrix UEqn (
fvm::ddt(rho, U)
fvm::div(phi, U)
turbulence-gt;divDevRhoReff(U)
==
-fvc::grad(p)
rho*g
fvOptions(rho, U)
);
第3章 燃烧机理
甲醇燃烧的全局方程为:
该全局反应仅代表理想化的燃烧反应物与产物。甲醇虽然是结构最简单的醇类,实际燃烧过程却是十分复杂的,包含了数百种中间反应与中间产物。燃烧机理,即燃烧过程的化学反应机理,通过将复杂燃烧过程分解为许多基元反应,从而厘清各中间反应与中间产物的关系。
3.1详细机理
在学术上,不同的甲醇燃烧机理有所区别,但都具有相似的反应过程并且有大量相同的中间产物,通过实验精确测定所得出的燃烧机理基本上都能够准确的代表燃烧过程。比较有代表性的甲醇燃烧机理是加州大学圣迭戈分校的San Diego机理。[12]而该机理包含数百个可逆反应,由第3章的讨论可以知道,求解如此多的反应方程在计算上较为困难,求解时间随反应步数线性增加。因此,保证计算精度要求的情况下,系统地简化燃烧机理是十分必要的。
3.2 简化版26步机理
敏感性分析是一种常用的简化燃烧机理的方法,即采用详细机理进行数值模拟,修改各基元反应的指前因子(化学反应速率与之成正比),分析其对最终结果的影响,删去影响程度不大的反应,从而实现简化。通过敏感性分析简化燃烧机理的优点是简化结果在燃烧特征、最终产物方面更接近详细机理,并且有助于对燃烧过程的概念理解。而存在的问题是,某些燃烧过程中十分重要但敏感度低的反应被简单的删去了,这会导致一些问题,比如说不能够实现自点火(autoignition)。一些简化甲醇燃烧机理以与自由基的反应作为初始反应:
忽略了点火初期反应产生自由基的一些重要但敏感度低的反应,而在甲醇-空气混合气中初始状态下是没有自由基存在的,这就导致在数值模拟中无法正常点火。
R. Seiser等人通过分析San Diego机理中各基元反应对点火条件的影响,删去了200多条对结果无影响的反应(如2或3碳原子的反应),经过迭代计算,最终确定了26条关键的不可逆反应,其中任何一条反应删去都会带来10%以上的误差。并且对比实验结果发现简化后的机理比较符合实验结果[11]。下文将该机理简称为RS-26机理,如表3.1所示。其中化学反应速率常数由Arrhenius公式计算:,为指前因子,为反应温度,为拟合率常数,为活化能,为摩尔气体常数。
在RS-26机理中,反应1为初始反应,该反应生成一些自由基后甲醇被反应2~5消耗。甲氧基不如羟甲基稳定,通过反应6转换为后者[14],同时甲氧基在反应8中分解,在反应9中被氧分子轰击。羟甲基同时在反应7中轰击氧分子。产生的甲醛在反应10~13中被消耗,其生成的甲酰基在反应14中与氧气反应,同时在反应15中分解。反应16为CO氧化过程,虽然该反应过程十分缓慢,但仍然有足够的放热量,因此是甲醇自点火过程的重要反应。通过过氧化氢产生自由基的反应17、18十分活跃,是非常重要的反应。与过氧羟基重组相关的反应17~24具有与反应2一致的重要性,应当在机理简化过程中保留,而与氢氧根重组相关的反应仅有25、26比较重要[15]。
简化后的26步反应已经比较适合于数值模拟,相比详细机理来说复杂度大大降低。但如果对计算性能有更高的要求仍可以通过分析各步反应对结果的影响继续进行简化,但必然会导致偏差值增大。人为地修改某些反应的反应速率可以达到缩小预测值偏差的目的,但属于偏向经验主义的做法。
序号 | 反应 | A | n | E |
1 | CH3OH O2 → CH2OH HO2 | 2.000e 13 | 0.000 | 44933.08 |
2 | CH3OH HO2 → CH2OH H2O2 | 8.000e 13 | 0.000 | 19383.37 |
3 | CH3OH H → CH2OH H2 | 1.354e 03 | 3.200 | 3489.48 |
4 | CH3OH OH → CH3O H2O | 4.400e 06 | 2.000 | 1505.74 |
5 | CH3OH OH → CH2OH H2O | 1.440e 06 | 2.000 | -838.91 |
6 | CH3O M1 → CH2OH M1 | 1.000e 14 | 0.000 | 19120.46 |
7 | CH2OH O2 → CH2O HO2 | 5.000e 12 | 0.000 | 0.00 |
8 | CH3O M1 → CH2O H M1 | 7.780e 13 | 0.000 | 13503.82 |
9 | CH3O O2 → CH2O HO2 | 4.280e-13 | 7.600 | -3537.28 |
10 | CH2O HO2 → HCO H2O2 | 4.110e 04 | 2.500 | 10205.54 |
11 | CH2O OH → HCO H2O | 3.900e 10 | 0.890 | 406.31 |
12 | CH2O O → HCO OH | 3.500e 13 | 0.000 | 3513.38 |
13 | CH2O H → HCO H2 | 5.740e 07 | 1.900 | 2748.57 |
14 | HCO O2 → CO HO2 | 7.580e 12 | 0.000 | 411.09 |
15 | HCO M2 → CO H M2 | 1.860e 17 | -1.000 | 16993.31 |
16 | CO OH → CO2 H | 4.400e 06 | 1.500 | -740.92 |
17 | HO2 HO2 → H2O2 O2 | 3.020e 12 | 0.000 | 1386.23 |
18 | H2O2( M3) → OH OH( M3) | 2.623e 19 8.153e 23 | -1.390 以上是毕业论文大纲或资料介绍,该课题完整毕业论文、开题报告、任务书、程序设计、图纸设计等资料请添加微信获取,微信号:bysjorg。 相关图片展示:
您需要先支付 80元 才能查看全部内容!立即支付
课题毕业论文、开题报告、任务书、外文翻译、程序设计、图纸设计等资料可联系客服协助查找。 最新文档
联系我们加微信咨询 
加QQ咨询 
服务时间:09:00-23:50(周一至周日) |