摘 要

前期研究表明，定向凝固制备的柱状晶Cu-Al-Mn形状记忆合金具有优异的超弹性性能和明显的性能各向异性特征，具有良好的应用前景。本文以柱状晶组织Cu-Al-Mn形状记忆合金的超弹性各向异性实验研究为基础，借助有限元分析软件ABAQUS对形状记忆合金进行数值模拟，采用用户子程序构造其本构关系，模拟了形状记忆合金的超弹性累加拉伸循环。同时通过对柱状晶组织Cu-Al-Mn形状记忆合金各向异性的几个特定角度进行了仿真计算，并与实验结果相比较。通过对任意角度对应的用户子程序参数的拟合和推导，实现了对柱状晶组织Cu-Al-Mn形状记忆合金各向异性的数值模拟，所得结果对于柱状晶形状记忆合金的超弹性各向异性仿真计算具有重要的指导意义。

本文的特色：观察柱状晶组织的结构，发现其与纤维增强复合材料有相似之处，参考单层板的偏轴工程弹性常数，计算柱状晶组织在任意角度的弹性模量。结合马氏体相变熵变和实验数据在任意角度拟合对应的相关参数。

关键词：形状记忆合金；柱状晶Cu-Al-Mn合金；超弹性各向异性；有限元数值模拟；用户子程序

Abstract

Columnar-grained (CG) Cu-Al-Mn shape memory alloys prepared by directional solidification shown in previous studies have excellent superelasticity and obvious performance anisotropy characteristics，and have a good application prospect．In this paper，based on the experimental study of the superelastic anisotropy of the CG Cu-Al-Mn shape memory alloy，the superelastic property of shape memory alloy is numerically simulated by the finite element analysis software ABAQUS．And the constitutive relation was constructed by the user subroutine to simulated the superelasticity of shape memory alloys in the accumulative tensile cycles．At the same time，the anisotropy of some specific angles in the CG Cu-Al-Mn shape memory alloy were simulated and compared with the experimental results．Through the fitting and derivation of user subroutine parameters corresponding to any angle, the numerical simulation of the anisotropy of the columnar crystal Cu-Al-Mn shape memory alloy is realized．The obtained results has important guiding significance for the superelasticity of the CG shape memory alloy．

The characteristics of this article：By observing the structure of the columnar crystal structure，it is found having similarities with the fiber-reinforced composite material．With refrence to the eccentric axis engineering elastic constant of the single-layer plate，we can calculate the elastic modulus of the columnar crystal structure at any angle．With reference to the martensitic phase transition entropy change and experimental data，parameters related with phase transition are fitted at any angle．

Key Words：Shape memory alloy；Columnar Cu-Al-Mn alloy；Superelastic anisotropy；Finite element numerical simulation；User subroutine

目　录

摘要 I

Abstract II

第1章 绪论 1

1.1 课题背景及目的意义 1

1.1.1 课题背景 1

1.1.2 目的及意义 1

1.2 Cu-Al-Mn形状记忆合金 2

1.2.1 形状记忆合金概述 2

1.2.2 形状记忆合金特性 3

1.3 形状记忆合金的本构关系 4

1.3.1 宏观唯象模型 5

1.3.2 细观力学模型 5

1.4 柱状晶Cu-Al-Mn合金的超弹性各向异性 6

1.5 研究内容和技术路线 7

1.5.1 研究内容 7

1.5.2 技术路线 8

第2章 有限元本构模型 10

2.1 热力学关系 10

2.2 动力学关系 12

2.3 相变条件 15

2.4 双线性超弹性模型 16

2.5 本章小结 17

第3章 超弹性数值模拟 18

3.1 数值算法 18

3.2 用户子程序 21

3.3 建模过程 22

3.4 模拟结果 22

3.5 复杂路径模拟结果 27

3.6 本章小结 29

第4章 各向异性的数值模拟 30

4.1 ABAQUS材料叠加网格实现各向异性 30

4.1.1 介绍 30

4.1.2 初步理论 31

4.2 确定任意方向材料参数以实现各向异性模拟 31

4.2.1 实验结果的数值模拟 32

4.2.2 参数计算 36

4.2.3 任意角度的数值模拟结果 43

4.3 本章小结 44

结论 46

参考文献 47

致谢 49

绪论

1.1 课题背景及目的意义

1.1.1 课题背景

国家重点基础研究发展计划（“973”计划）的“高性能金属材料控制凝固与控制成形的科学基础”项目（2011CB606300）中提出了一种利用成型加工发展组织异向性，从而显著提高金属材料性能的创新性研究思路^[1]。普通多晶组织Cu基形状记忆合金具有变形协调性差，容易发生晶间开裂的缺点。现以定向凝固制备的柱状晶组织Cu基形状记忆合金，具有极好的变形协调性和相变协调能力，这有利于发展低成本高性能的Cu基形状记忆合金。

柱状晶Cu-Al-Mn形状记忆合金采用定向凝固方法制备，具有轴向强lt;001gt;取向和低能平直晶界的特征，超弹性应变可达到单晶合金水平，具有替代Ni-Ti合金的潜力，同时其成本不到Ni-Ti合金的十分之一^[2]。

柱状晶组织Cu-Al-Mn合金具备优良的超弹性，同时也具有显著的各向异性，其力学性能在与柱状晶凝固方向所成不同角度的方向上有所不同，呈现出明显的差异。本文为了和实验研究超弹性各向异性性能相结合，采用计算模拟仿真的方法研究在更多的方向和应力状态下合金的超弹性。单纯靠实验方法很难表征所有应用状态下的力学行为，数值计算仿真可以在一定程度上解决复杂力学行为的分析。

1.1.2 目的及意义

本文参考柱状晶组织Cu-Al-Mn形状记忆合金的实验研究，针对其具有的超弹性各向异性，以单向拉伸数据为基础，采用力学本构模拟的方法，建立起合金的本构模型，并在有限元软件ABAQUS中结合用户子程序进行相应的各向异性力学行为的计算仿真。

通过对比多组实验曲线和有限元模拟结果，如各个取向试样的超弹性累加拉伸、复杂加载路径下的应力-应变曲线，验证有限元模型的稳定性和可靠性。通过研究与形状记忆合金的超弹性各向异性相关的力学参数，如奥氏体弹性模量、马氏体弹性模量、相变应变和相变应力，实现对柱状晶组织形状记忆合金任意角度下的超弹性各向异性的数值模拟。本研究的完成可推进形状记忆合金超弹性本构方程的应用，同时为柱状晶组织合金的各向异性性能的实验研究及其应用提供理论参考和指导。

1.2 Cu-Al-Mn形状记忆合金

1.2.1 形状记忆合金概述

形状记忆合金（shape memory alloy，SMA）作为一种智能型功能材料，既有传感功能（感知和接收应力、应变、电、热等信号），又有驱动功能（响应激励）^[3]。

它具有在温度变化和应力诱导下产生可逆的马氏体相变的特点，这是SMA的形状记忆效应（shape memory effect，SME）和超弹性（superelasticity，SE）两种重要的功能特性的物理基础。该合金还具阻尼效应和电阻效应，以及良好的生物相容性、无磁性、高阻尼、耐腐蚀和磨损、比强度高等性质^[4]。现已广泛应用于航空航天、土木建筑、生物医学以及日常生活等众多领域，可以实现结构的振动控制、主被动变形控制以及结构检测等等。

目前的SMA合金材料大致可以分为Fe基、Ni-Ti基和Cu基三大类形状记忆合金。以这三大类合金为基础添加其他元素，可以改善或实现合金的某方面特性。

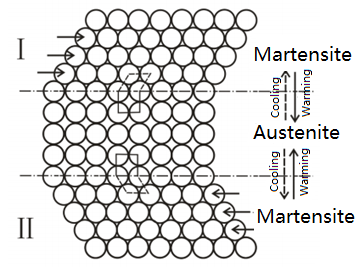
图1.1　马氏体相变的简化模型^[2]

Figure1.1　A simplified model of martensitic transformation

形状记忆合金的特殊行为诞生了几种工业应用，如生物机械植入物，执行器和隔振器。这种行为是固-固相转化的结果，称为马氏体相变。由于温度变化，SMA微观结构在两个稳定状态之间转换，即低温马氏体和高温奥氏体，如图1.1所示，这种相变在宏观尺度上会导致各种力学行为。

Cu基形状记忆合金是除Ni-Ti合金之外较具应用前景的形状记忆合金，而且材料价格低廉，只有Ni-Ti合金的十分之一。但其相应的普通多晶组织性能较差，容易在应力作用下的马氏体相变完成前就发生晶间脆性断裂，此外，还存在疲劳强度低，冷加工性能差，表观超弹性应变极限值低等缺陷，具有极大的局限性。在另一方面，Cu基形状记忆合金单晶体具有可以与Ni-Ti基合金相媲美的性能，但大尺寸的Cu基单晶的制备非常困难，难以大规模应用。

通过合理的组织结构设计，降低多晶Cu基合金中多晶晶粒的取向差异，有利于提高晶粒间的相变协调性和变形协调性，相当于用较为简单有效方法使Cu基合金在某一方向贴近单晶性能，从而改善普通多晶组织合金的超弹性、形状记忆效应和耐疲劳性能。

1.2.2 形状记忆合金特性

由马氏体相变行为导致的主要宏观力学特性有^[6]：

（1）单向形状记忆效果（one way shape memory effort，OWSME）：在给定温度下施加荷载产生永久变形，通过适度加热，恢复初始形状的能力。

（2）双向形状记忆效果(two way shape memory effort，TWSME)：记忆两种形状能力，一种在低温，另一种在高温下，通过足够的热机械训练，不但对奥氏体母相具有记忆效应，并且在冷却后也能恢复马氏体变形后的形状。

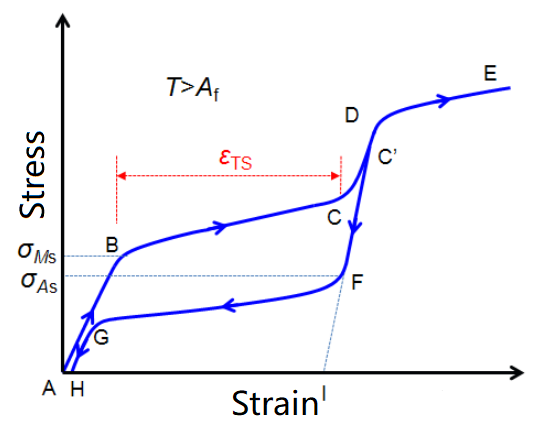
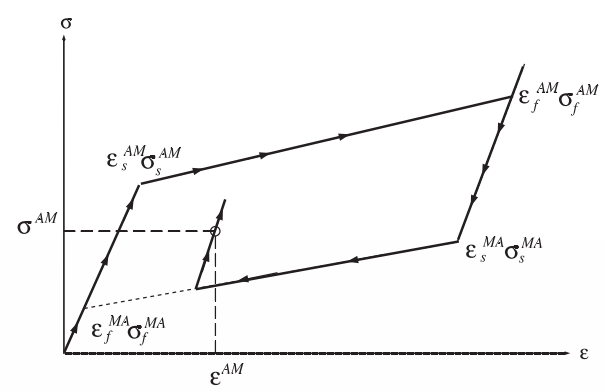
图1.2　超弹性应力-应变曲线示意图^[2]

Figure1.2　Superelastic Stress-Strain Schematic

（3）超弹性效应：一定条件下，合金在应力作用下产生弹性变形后继续发生更大的非弹性变形，此时出现不稳定的应力诱导马氏体；卸载后，马氏体相会恢复到之前的奥氏体母相，合金随之恢复到变形前的形状。其可恢复应变量大（gt; 5%），且应力-应变关系呈现出非线性，其曲线由于相变应变的存在呈滞回环形式，如图1.2所示。

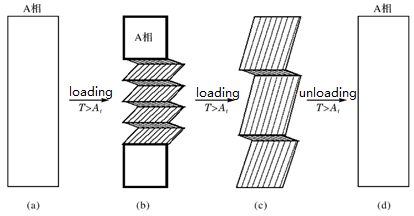
图1.3　超弹性机制^[6]

Figure1.3　The mechanism of superelasticity

超弹性相变机制如图1.3所示，温度在马氏体逆相变结束温度A_f以上时，材料处于奥氏体相，此时加载外力产生的应力诱发马氏体相变处于热力学不稳定的状态，对应的奥氏体相是稳定状态，所以在卸载后马氏体将发生奥氏体逆相变^[5]。（a）表示奥氏体相状态，（b）中应力诱发产生取向不同的马氏体变体，材料出现宏观变形，（c）中继续施加应力，材料全部变为马氏体相，（d）中进行卸载，材料发生逆相变，变形完全恢复^[6]。

1.3 形状记忆合金的本构关系

为了在ABAQUS中实现材料的力学性能，需要导入SMA的本构关系。由于SMA行为的特殊性，以及缺乏这些材料在复杂行为下的实验数据，难以描述其本构关系。直到超弹性的相变理论在1979年被提出，相关研究才得以展开，至今已有多种理论和方法，构造了不同类型的本构关系来模拟SMA的行为。

实际应用中比较有影响力的本构模型主要有以广义塑性理论为基础的宏观唯象模型以及基于马氏体相变晶体学和热力学原理的细观力学模型^[6]。

1.3.1 宏观唯象模型

该模型建立在实验基础上，通常由经验公式组成，并使用易于实验测量的参数，由于其简单性，非常合适用于数值计算。模型受限于多轴实验数据的缺乏，主要是一维的宏观SMA本构模型，然后推广到三维，再现其单轴力学行为，但由此得到的形状记忆合金三维性能的可信度很难确定。这类本构模型的区别主要在于其中所采用的相变动力学公式，应用较多的有Tanaka模型、Liang-Rogers模型和Brinson模型。

Tanaka模型在实际应用过程中仅限于一维情况，采用的是指数形式的马氏体相变公式，认为马氏体体积分数ξ与温度T呈关系，以此描述相变程度。Liang-Rogers模型采用全量型的本构关系，是在Tanaka模型的基础上得到，推广到了三维情况。Liang-Rogers模型的缺陷在于，当温度低于马氏体相变结束温度M_f时，材料呈线弹性。正是基于这个原因，Brinson将马氏体体积分数分为应力诱发的马氏体体积分数和温度诱发的马氏体体积分数两部分，分别对应采用两个变量，Brinson模型中马氏体相变动力学方程在不同温度区间各有两个演化方程^[6]。这三个模型在本质上都是基于能量守恒的。

这些模型形式简单，适用于工程实际应用，但只描述了合金宏观行为，不涉及单晶和多晶，不能描述材料变形过程和相变机理，没有考虑各向异性行为，而细观力学模型在这方面做的更好^[7]。

1.3.2 细观力学模型

该模型采用热力学基本原理，其基本概念是通过描述微观结构和基本形变机制确定宏观行为。在这些模型中，Patoor，Sun-Hwang，Brinson等人^[8]的模型值得参考，这些模型考虑马氏体变体作为相变内含物，使用微观力学来计算相变导致的相互作用能（interaction energy）并以此描述材料的热弹性马氏体相变，以平均值计算应力和应变，考虑内含物代表可能的变体。该类模型具体的物理基础使他们更具实际意义，同时建立了宏观力学行为的理论依据，然而，考虑到涉及到的重要参数的数量，这类推导相当复杂并且对计算时间要求过高。

Sun-Hwang模型引入相变塑性以模拟SMA材料的形状特性，缺点是将重定向和相变过程中的自由余能和能量耗散分开来讨论，这不利于描述整体行为^[8]。Patoor模型采用晶体学考虑马氏体相变的微观结构，以各个马氏体变体的体积分数作为内状态变量，通过吉布斯自由能函数和不同马氏体晶粒间的交互作用矩阵来计算单个晶体和晶粒的行为，再通过自洽方法推广到多晶行为^[9][10]。

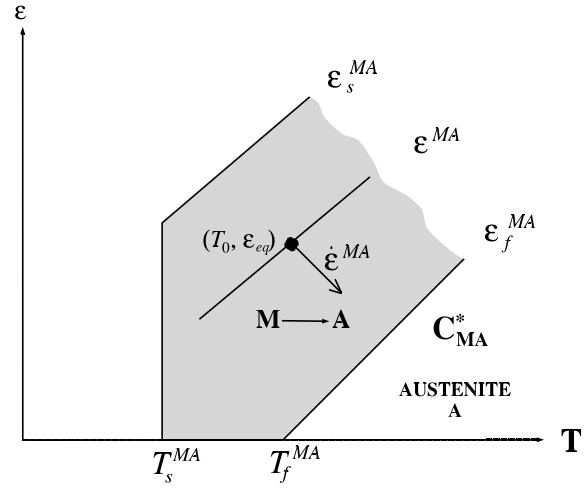
1.4 柱状晶Cu-Al-Mn合金的超弹性各向异性

本文的具体研究对象是由定向凝固方法制备的具有大晶粒尺寸、高取向性组织和平直晶界形貌的柱状晶Cu-Al-Mn形状记忆合金。该合金的超弹性应变可达到单晶合金水平，克服了普通多晶组织Cu基合金由于变形协调能力差，易发生晶间断裂而导致记忆性能差，从而限制合金广泛应用的问题^[11][12]。

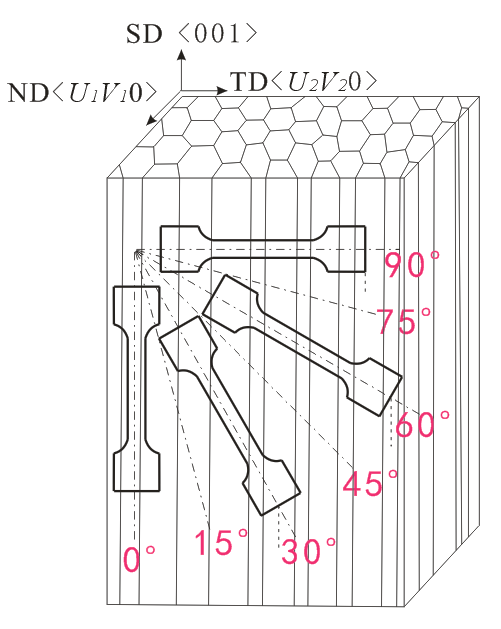
柱状晶（columnar-grained，CG）组织是一种极端各向异性组织，与柱状晶凝固方向所成的不同角度上的力学性能有所变化。合金沿凝固方向（SD）为长径比很高的柱状晶晶粒，有的柱状晶晶粒甚至贯穿将近整个铸锭。图1.4为定向凝固制备的柱状晶组织Cu-Al-Mn合金（CG-CAM）试样的横截面（与SD垂直）和纵截面（与SD平行）的金相组织形貌照片。CG-CAM试样横截面的组织形貌与普通等轴晶相似，平均晶粒直径约为1000μm左右；而其纵截面晶界平直，只存在纵向晶界，基本不含横向晶界和三叉晶界^[2]。因此，通过定向凝固制备的柱状晶Cu-Al-Mn形状记忆合金在力学性能的到优化的同时也具有了显著的宏观各向异性，其力学性质随着与柱状晶凝固方向所成角度的改变而有所改变，在不同的方向上呈现出明显的差异^[2][13]。

图1.4　定向凝固柱状晶组织Cu-Al-Mn合金的金相形貌照片^[2]

以上是毕业论文大纲或资料介绍，该课题完整毕业论文、开题报告、任务书、程序设计、图纸设计等资料请添加微信获取，微信号：bysjorg。

相关图片展示：