对光晶格中费米-费米混合奇异量子态转变温度的计算毕业论文
2020-04-07 14:13:28
摘 要
本文在简要介绍了二次量子化以及平均场论的基本内容的基础上,着重对哈伯德模型进行了分析,并利用费米-哈伯德模型对在光晶格中半满情况下的费米-费米混合体系进行了描述,运用平均场近似,对系统的哈密顿量进行了简化,从而分别在零温和有限温的情况下对系统的可能的量子相展开了讨论。
在零温下,通过求解系统序参量的自洽方程得到了序参量的表达式,从中可以看出,此时系统总是倾向于处在一种自旋排列相互交错的有序状态。
在有限温下,得到了系统序参量的自洽方程,可以根据该方程数值地求解量子相变温度,并计算了系统的配分函数和自由能,得到了自由能对系统参数的依赖关系,从而为实验提供了确切的理论依据。
关键词:费米-费米混合;哈伯德模型;光晶格;平均场理论
Abstract
After a brief introduction of second quantization and mean-field theory, we direct our attention to Hubbard model and describe the fermi-fermi mixture in the optical lattice at half-filling by Fermi-Hubbard model. We perform mean-field approximation to simplify the Hamiltonian and discuss the possible quantum phases of this system at absolute zero temperature and finite temperature respectively.
At absolute zero temperature, we obtain the expression of the order parameter by solving the self-consistent equation of it. The result shows that in this case the system always tends to stay in an ordered state where spin is arranged alternately.
At finite temperature, we get the self-consistent equation of the order parameter, from which we can compute the phase transition temperature numerically. Then, we derive the partition function and the free energy as a function of system parameters. The results provide a helpful theory evidence for the experiment development.
Key Word: fermi-fermi mixture; Hubbard model; optical lattice; mean-field theory
目 录
摘 要 I
Abstract II
第一章 绪论 1
1.1 国内外的研究现状 1
1.2 研究的目的与意义 3
第二章 二次量子化 5
2.1 全同粒子 5
2.2 占有数表象 6
2.3 产生与湮灭算符 6
2.4 二次量子化算符的一般形式 7
2.5 二次量子化中的基矢变换 8
2.6 量子场算符及其傅立叶变换 9
第三章 哈伯德模型 11
3.1 费米-哈伯德模型 11
3.2 玻色-哈伯德模型 12
第四章 平均场理论 14
4.1 数学形式 14
4.2 对称破缺 15
第五章 费米-费米混合体系 18
5.1 零温下的费米-费米混合体系 19
5.2 有限温下的费米-费米混合体系 23
第六章 结论 25
6.1 总结 25
6.2 展望 26
参考文献 27
致 谢 29
第一章 绪论
1.1 国内外的研究现状
超冷原子物理是上世纪末发展起来的一个新兴研究领域,其研究的对象为接近绝对零度的稀薄气体。1995年,玻色-爱因斯坦凝聚(BEC)被预言七十年后终于在实验室实现,自此超冷原子物理进入了飞速发展的时期,对超冷玻色气体和费米气体的研究成为了当代物理最活跃的领域之一。
最初的量子气体实验主要是在铷、钠或锂上进行,到目前为止,已经在多种原子体系中实现了玻色-爱因斯坦凝聚,比如1H、7Li、23Na、39K、41K、52Cr、85Rb、87Rb、133Cs、170Yb以及处于激发态的4He[1]。可以看到,随着在玻色气体中BEC的实现,对超冷费米气体的研究也逐渐受到关注。费米气体指的是自旋为半整数并且与玻色气体具有截然不同量子统计特性的气体,其量子行为和自然界中的中子、质子和电子等基本费米子具有统一性,因此可以用来研究原子分子物理中的电子行为、凝聚态物理中超导与超流以及粒子物理与天体物理中的强关联行为[2]。相比冷却玻色气体而言,在实验上冷却费米气体要面对更大的困难,一方面是由于过于相信费米子之间没有相互作用,另一方面是由于蒸发冷却技术很难应用到费米系统,因为蒸发冷却技术主要通过弹性碰撞后能量重新分配来实现BEC,由于泡利不相容原理,全同费米子之间的s波散射是被禁止的,尽管一般情况下p波散射没有被禁止,但是由于其对温度平方的依赖性而被强烈地抑制了。当前在实验上主要采用两种方法实现简并费米气体:其一是克服泡利不相容原理通过不同自旋的原子之间的碰撞来实现;其二是同时陷俘玻色和费米气体,利用同步冷却技术来实现[3]。于1999年,美国JILA研究所在磁阱中囚禁不同自旋态的原子,利用蒸发冷却技术首次在实验上实现了超冷简并费米气体[4]。
随着理论研究和实验技术的发展,实验的体系不再局限于仅由玻色子、费米原子或者费米分子气体组成的体系,而是逐渐推广到对杂核体系的量子简并的研究,例如两种或者三种玻色子的混合物、玻色子和费米子的混合物以及两种不同的费米子的混合物等等。其中,玻色-费米混合体系已经在6Li-7Li、6Li-23Na以及40K-87Rb等体系展开了研究。同时,40K-40K和6Li-6Li费米-费米自旋混合气体在实验上已经观察到了金属和Mott绝缘态以及BCS-BEC转变[5],在6Li-40K费米-费米混合体系中简并费米气体与杂合分子已经成为了现实,实现更多费米-费米混合体系并设法观察到新奇量子态始终是研究的重要目标,未来还希望能够实现由161Dy、163Dy或167Er组成的费米-费米混合体系,然而在实验技术的发展上仍然存在许多困难[6]。尽管在实验上一直未能实现费米气体的奇异超流相,在理论上仍然受到了许多关注,p波超流、不平衡超流、杂合库珀对超流或是自旋轨道耦合费米超流都是理论上存在的几种可能,也成为了实验上努力的方向。
目前,已经发展了多种调控体系参量的有效手段。通过Feshbach共振直接调节原子之间的有效散射长度从而改变原子间的相互作用,对BCS-BEC转变、形成寿命更长的BEC分子、配对空缺、不均匀气体等的研究逐步得到深入[7]。此外,光晶格可以说是操控量子气体最重要的工具,它最初是在激光光谱学的背景下提出,随着激光冷却技术的发展,在实验上实现成为了可能。光晶格将超冷原子气体束缚在一个周期势场中,和真实固体中的晶格类似,不同的是,光晶格提供的是一个十分纯净且无缺陷的系统,同时相关参数具有很高的可调控性,这就为量子模拟提供了一个非常理想的平台,成为了揭示新奇量子效应的至关重要的一种手段[8]。
近年来,哈伯德模型成为了描述光晶格中的超冷原子气的重要模型,模型的哈密顿量形式简洁,仅仅考虑了占据同一个格点的粒子之间的相互作用以及粒子在最近临格点之间的跳跃,该模型最早在1963年提出来描述固体中的电子体系并且对研究高温超导的机制有重要意义。在固体的情况下这个模型忽略了长程的库伦相互作用、晶体的缺陷以及晶格的扰动,因此只是一种非常粗略的近似,从而不能反映出一些重要的物理效应[9]。然而,哈伯德模型可以非常有效地描述光晶格中的超冷原子体系,根据体系中的粒子种类,可以将哈伯德模型分为玻色-哈伯德模型和费米-哈伯德模型。相对来说,费米-哈伯德模型无论是在排斥相互作用的情况还是在吸引相互作用的情况都有着更加丰富的内容,费米子的统计特性以及自旋自由度的影响都是这些有趣的物理现象背后的原因。费米-哈伯德模型在光晶格中的实现,直接将量子气体的研究前沿与凝聚态物理联系了起来。
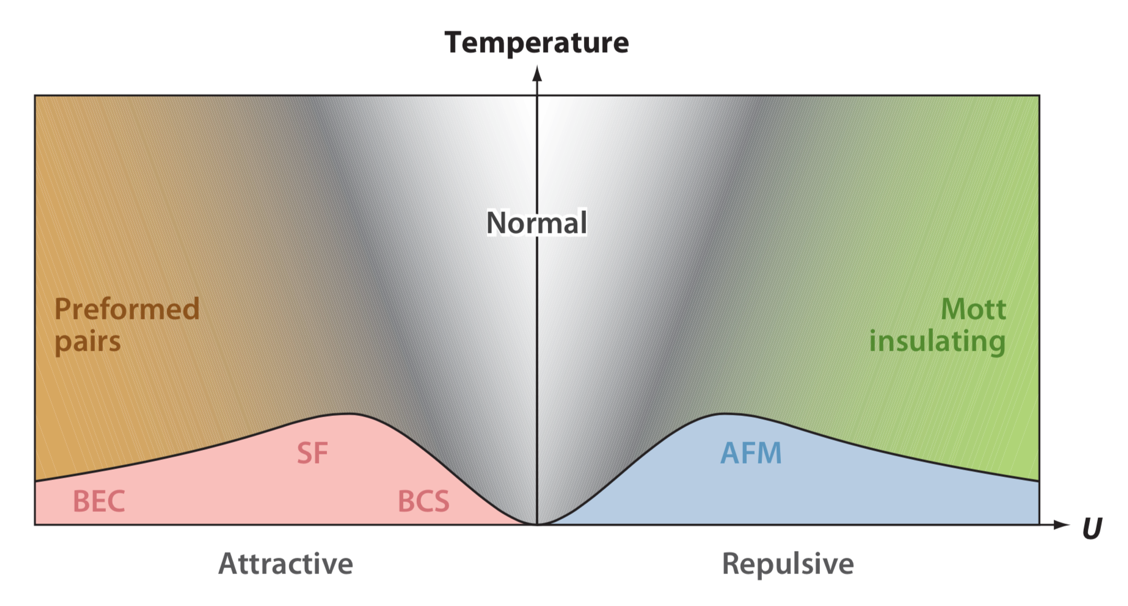
图1.1 在三维简单方晶格半满情况下费米-哈伯德模型的相图[10]
图1.1给出了费米-哈伯德模型的一个比较完整的相图。吸引相互作用的费米-哈伯德模型,也就是占据同一个格点的费米子之间的相互作用能量为负值的情况,已经在超导的背景下被广泛地研究。在低温时通过调节相互作用的强弱可以使s波超流体发生BEC-BCS转变,但在实验上还无法达到足够低的温度来实现这种转变。BCS通常是发生在弱相互作用的情况并且临界温度随着相互作用的增强而升高,随着相互作用的增强,配对粒子逐渐转变为BEC的情况,可以将每一对看作是一个硬核玻色子,这时,临界温度随着相互作用的增强而降低。
在排斥相互作用的情况下,费米-哈伯德模型呈现出的最重要的两种状态是Mott绝缘体和反铁磁序的出现。在较高的温度时,自旋处于一种无序的状态,从而导致系统基态具有十分高的简并度,此时系统可以从弱相互作用下的金属费米液体转变到强相互作用下的Mott绝缘体。在金属态中,原子可以在晶格中自由运动;而在Mott绝缘态中,原子被限制在格点中,并且由于泡利不相容原理和排斥相互作用的影响,两个原子占据同一个格点的情况受到抑制。在低温时,系统的自旋变为一种有序的状态,即相邻格点之间总是倾向于被自旋相反的粒子占据,这是因为粒子在相邻格点之间的虚跳跃能使系统的能量更低。处于Neel临界温度时,发生二级相变使系统转变到反铁磁序的状态。当相互作用很弱时,系统会形成自旋密度波,并且Neel临界温度非常低;随着相互作用逐渐增强,系统便随之呈现出反铁磁Mott绝缘态。在实验上已经观察到了Mott绝缘体以及短程的反铁磁序,同样是由于温度的原因,自发形成的长程反铁磁序至今还未实现[11]。此外,为了解决在二维参杂哈伯德模型中非传统超导这个长期以来一直被关注的问题,需要达到更低的温度。已经有预言说在这种参杂的情况下会出现d波超流态,但不论是在实验上还是在理论上仍然有待进一步研究。因此,发展有效的冷却技术是实验上所面临的一个重大挑战,同时在理论上对如何获得更高的临界温度的计算也成为了需要关注的问题。
1.2 研究的目的与意义
本次毕业设计的主要目标是计算二维光晶格半满情况下费米-费米混合奇异量子态的转变温度,具体将进行如下几项工作:
I.查阅相关文献,学习基础专业知识,掌握二次量子化、量子场论的基本内容,了解强相互作用费米-费米混合的量子场论模型描述,重点学习哈伯德模型,并利用该模型对光晶格中的费米-费米混合体系进行描述。
II.分析费米-费米混合在光晶格半满的情况下可能的量子相,研究排斥相互作用可能导致的量子密度波态,研究自发对称破缺机制;
III.考虑零温下的费米-费米混合体系,运用平均场理论,求解哈密顿量,得到基态波函数,求解系统序参量的自洽方程;
IV.运用平均场理论,计算出费米-费米混合的有限温相变,计算该系统有限温的配分函数和自由能,建立有限温多体理论,得到系统自由能对系统参量的依赖关系。
对相变临界温度的计算可以为实验上费米-费米自旋混合气体奇异量子态的实现提供更确切的理论依据,对进一步研究混合简并气体有着重要意义。
第二章 二次量子化
2.1 全同粒子
在经典力学中,如果已知充分的初始条件,那么随后粒子的状态就可以由哈密顿运动方程所决定。由于粒子的轨道可以被准确地计算,在任一时刻,都有确定的位置和速度,因此粒子总是可区分的。在这种意义上,在经典力学中,即使是全同粒子(具有完全相同的质量、电荷、自旋等固有性质)也是可以被区分的。
在量子力学中,情况就完全不同了。由于不确定原理,粒子不存在确定的运动轨道,而是像波包一样传播。在运动过程中,全同粒子的波函数在空间发生重叠,由于它们的固有性质完全相同,位置和速度又不像经典粒子那样同时具有确定的值,这就导致了全同粒子的不可区分性。由于这一特性,使得在全同粒子所组成的体系中,两个粒子相互代换不引起物理状态的改变。这个论断被称为全同性原理,是量子力学中的基本原理之一[12]。
根据全同性原理,与描述的是同一个状态,因而它们之间只相差一个常数因子,则
由此得到,依次对应物理中可能的两类粒子,即所谓的玻色子和费米子:
因此,描述全同粒子体系状态的波函数只能是对称的或反对称的。
任何描述N个粒子的波函数都可以写成这N个单粒子波函数的线性叠加,同时考虑上述的波函数对称性,可以证明,N粒子的波函数有如下形式:
其中,对于费米子,对于玻色子;代表处于态的总粒子数;表示如果将置换到的过程中需要交换两个元素的次数为偶数(奇数),其值取;求和包含了对量子数集所有的种置换的求和。
2.2 占有数表象
为了能够更加简洁地描述N个全同粒子的状态,引入了占有数表象,通过依次列出占据每一个状态的粒子数而得到N粒子波函数的基矢,
从而避免了对每一个粒子的状态都要进行标记的繁杂。
随后,很自然地就引入了粒子数算符,其本征态为,对应的本征值为占据第个态的粒子数,即
对于费米子,由于泡利不相容原理,仅能取0或1;对于玻色子,可取任意自然数。
对于空间中没有粒子的状态,用真空态来标记。
2.3 产生与湮灭算符
为了将一次量子化和二次量子化联系起来,定义算符,
其中,。可以看出,经过算符作用后,体系中占据第个状态的粒子数增加了1个,因此将称为产生算符。
需要注意的是,对于费米子,每个态上至多有1个粒子,因此有。
相应地,定义湮灭算符,
它们与粒子数算符的关系是
通过将产生算符多次作用到真空态,可以得到N粒子波函数的任意基矢,
根据产生于湮灭算符的定义,容易得到它们之间的对易关系
其中,,对应于玻色子;,对应于费米子。
2.4 二次量子化算符的一般形式
在二次量子化中,所有的算符都可以由前一节中定义的产生和湮灭算符所表示。
首先,考虑作用在N粒子系统上的单粒子算符,通常都具有这种形式
其中,是作用在第n个粒子上的单粒子算符。例如,动能算符,其中是作用在第n个粒子上的动量算符。
对于在基矢中已对角化子的单粒子算符,有
根据这个定义,可以得到
则在二次量子化中,单粒子算符的一般形式为
在一般的基矢中,则有更加一般的形式
上述过程可以推广到多粒子算符中。对于二粒子算符,在二次量子化中的一般形式为
其中,。

图2.1 单粒子算符和二粒子算符在二次量子化中的示意图。指向内和指向外的箭头分别代表初态和末态
2.5 二次量子化中的基矢变换
一个量子态可以采用各种不同的表象来描述,作为对量子态进行运算的算符,在不同的表象中也有不同的表述形式,这就使得基矢的变换成为量子物理中一个重要的问题。
现在考虑两组不同的完备的单粒子基矢集和,利用完备性关系,以及和,便可以得到不同基矢下产生和湮灭算符之间的变换规则:
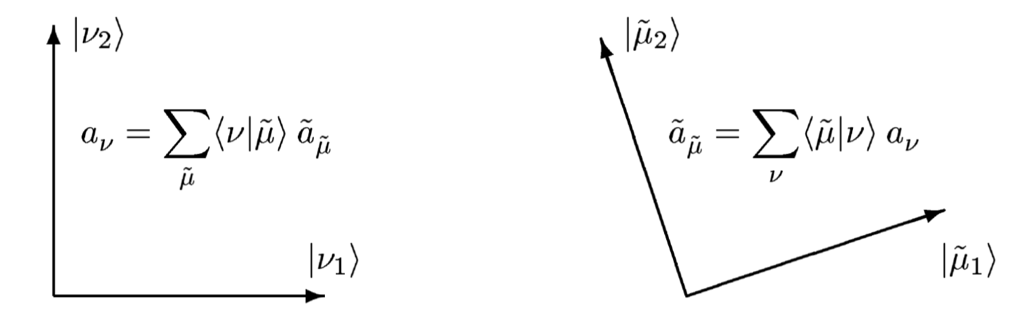
图2.2 湮灭算符和在基矢和之间的变换规则
2.6 量子场算符及其傅立叶变换
在二次量子化中,有一个特殊的表象需要引起注意,就是实空间表象。在实空间表象中,完备的基矢的本征值不再是离散的量子数,而是连续的位置矢量,即基矢集变为,相应地,产生和湮灭算符就是所谓的场算符和,它们和其他表象下的产生湮灭算符之间有如下的变换规则:
需要注意区分的是,和是二次量子化算符,而和是一次量子化中的波函数。
在某种意义上,场算符体现了量子物理中波粒二象性的本质。一方面,它们被定义为场,也就是一种波;但另一方面,它们也具有类似粒子的对易关系:
通过引入场算符,可以非常方便地写出在实空间表象中的算符,将与带入二次量子化的单粒子算符的一般形式中,可以得到
因此,在实空间表象中,利用场算符表述时,二次量子化的算符具有和一次量子化矩阵元相类似的形式。
最后,在处理具体问题时,常常需要在实空间和动量空间之间转换,场算符可通过对动量空间中的产生和湮灭算符进行傅立叶变换得到
经过傅立叶逆变换,有
第三章 哈伯德模型
由于强关联多体系统的复杂性,想要对真实的系统进行研究是不现实的。因此,为了对相关体系进行研究,对真实系统进行合理的简化以构建有效的模型,成为了一个至关重要的问题。一般在构建模型的过程中,会忽略很多次要因素,例如粒子之间的远程相互作用,但是最重要的物理机制仍然被保留下来,从而能够有效地描述我们所关心的系统。在处理具体问题时,选择一个合适的模型是非常重要的。自1963年哈伯德模型被提出以来,它始终是研究多体物理的最简单有效的模型之一,曾正确地预言了Mott绝缘体的存在,也在研究高温超导的机制中备受关注。哈伯德模型最初是用来描述固体中的电子,可以看作是由紧束缚模型发展而来。由于哈伯德模型能够很好地近似描述低温时处于周期势场中的粒子,近年来,它也成为了研究光晶格中超冷原子体系的重要模型[13]。
3.1 费米-哈伯德模型
费米-哈伯德模型仅仅考虑在晶格中占据同一个格点的费米子之间的相互作用,以及费米子在最邻近晶格格点之间的跳跃,因此该模型的哈密顿量有如下形式:
其中,为晶格格点位矢; 表示和为最邻近的格点;,标记自旋向上和自旋向下的同种费米子,也可指代两种费米子;、和分别为格点上费米子的产生算符、湮灭算符和粒子数算符;是费米子在最邻近格点之间的跳跃强度;为占据同一格点的费米子之间的相互作用强度,若则为排斥相互作用,若则为吸引相互作用。
课题毕业论文、开题报告、任务书、外文翻译、程序设计、图纸设计等资料可联系客服协助查找。



