基于切削力模型和特定切削条件的排屑角突变建模毕业论文
2020-04-08 13:25:37
摘 要
基于不等分剪切区理论,本文首先推导了直角切削的切削力和切削功率的预测模型,接着利用等效平面法,推导了在斜角切削的情况下的预测模型。以斜角切削的预测模型为基础,在假定切削过程服从最小能量原理,且刀尖圆弧半径不为0的条件下,本文推导了斜角双刃横车端面的主、副切削刃以及圆弧切削刃的切削层参数,建立了整体的切削力和排屑角预测模型,并借助MATLAB编程实现了相关算法。最后,以斜角双刃横车端面的预测模型为基础,在刀尖圆弧半径为0的条件下,在MATLAB上用优化算法求解了以切削宽度和切削厚度为控制参数时排屑角突变的分叉集。
计算结果表明,推导的直角切削模型的切削力预测在一定范围内精度较高,与实验对比误差在以内;推导的斜角双刃横车端面的模型,可以实现对切削力和排屑角的预测;推导的排屑角突变的分叉集,可以实现对排屑角突变情况的预测。
以数学建模和MATLAB编程为主,本文将前人的直角切削的切削力预测模型推广到了斜角切削且刀尖圆弧半径不为零的情况,并且利用优化算法成功拟合出了分叉集,扩展了切削力和排屑角突变的预测范围。
关键词:切削力模型;不等分剪切区理论;最小能量原理;排屑角突变
Abstract
Based on the theory of unequally divided shear zone, this paper first deduces the prediction model of cutting force and cutting power in orthogonal cutting, and then uses the equivalent plane method to derive the prediction model in the case of oblique cutting. Based on the forecast model of oblique cutting, under the condition that the cutting process obeys the principle of minimum energy and the arc radius of the tip is not zero, the main and auxiliary cutting edges and the circle of the beveled double-edged planer are deduced. The parameters of the cutting edge of the arc cutting edge establish the overall prediction model of the cutting force and the flowing chip angle, and the related algorithm is implemented by the simulation software MATLAB. Finally, on the basis of the prediction model of the inclined double-edged flat car end face, under the condition that the radius of the cutting edge arc is 0, the optimization algorithm is used on MATLAB to find out the control parameters when the cutting width and cutting thickness are used as the control parameters. Bifurcation set of mutated corners.
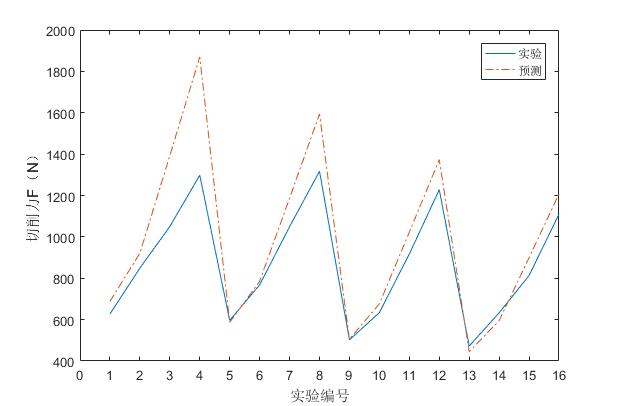
The calculation results show that the predicted cutting force of the right-angled cutting model has a high precision in a certain range, and the error is within ±10% compared with the experiment. The model of the inclined-edge double-edged flat-car end can achieve the cutting force and row. The prediction of the chip angles; the derivation of the bifurcation set of the chipping angle mutations can be used to predict the abrupt change of the flowing chip angle.
Based on mathematical modeling and MATLAB programming, this paper extends the cutting force prediction model of the right-angle cutting to the case of oblique cutting and the radius of the tool tip arc is not zero, and successfully uses the optimization algorithm to fit the bifurcation. The set extends the prediction range of cutting force and chipping angle mutations.
Key Words:Cutting force model;the theory of unequally divided shear zone;the principle of minimum energy;the mutation of the flowing chip angle
目 录
摘 要 I
Abstract II
第1章 目的及意义 1
1.1研究目的和意义 1
1.2国内外研究现状 1
1.2.1突变理论简介 1
1.2.2突变理论的应用 3
1.2.3排屑角预测研究现状 4
1.2.4切削模型研究现状 4
第2章 直角自由切削的切削功率 6
2.1基本假设与原理 6
2.2速度关系 6
2.3剪切变形关系 7
2.4温度关系 9
2.5切削力与切削功率的计算 10
2.6 MATLAB仿真分析与验证 10
第3章 斜角切削的切削功率 13
3.1切削功率的计算 13
3.2相关参数的取值 16
3.2.1材料特性参数 16
3.2.2剪切区厚度 16
3.2.3剪切角和摩擦角 16
第4章 斜角双刃非自由横车端面的切削功率 18
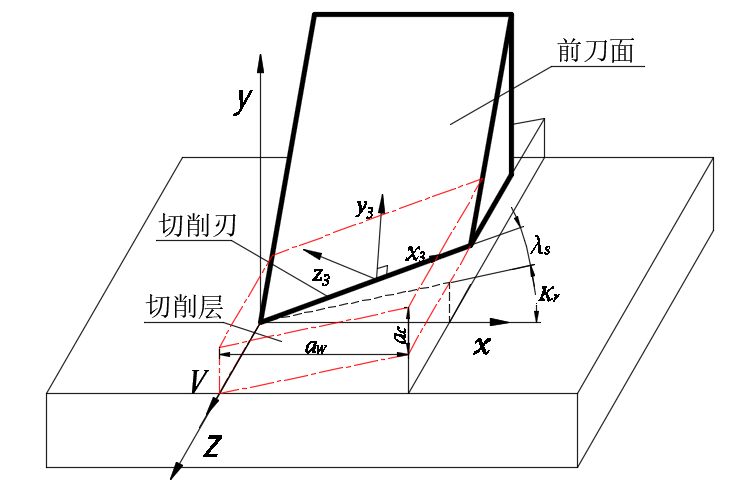
4.1切削刃角度参数的推导 18
4.1.1主切削刃的角度参数 19
4.1.2圆弧切削刃的角度参数 19
4.1.3副切削刃的角度参数 21
4.1.4排屑角和法向前角的推导 22
4.2切削层面积参数的推导 23
4.2.1情况1 23
4.2.2情况2 25
4.2.3情况3 29
4.2.4情况4 32
4.3总切削功率的推导 36
4.4 MATLAB仿真分析 39
第5章 0圆角直角双刃横车端面的排屑角突变 41
5.1直角双刃横车端面的切削功率 41
5.2 MATLAB仿真分析 42
参考文献 45
致谢 46
附录 47
第1章 目的及意义
1.1研究目的和意义
近年来,随着机械、材料和自动化等领域的进一步交融和进步,切削加工技术,包括高速切削技术、精密加工技术和微细制造技术等有了迅猛的发展,这也就要求切削基础理论的需要新的进展和突破。
传统切削理论认为,当确定了切削宽度 、厚度 、切削速度和刀具几何形状等控制参数时,切削过程的切削力、排屑角等状态变量也就相应确定了,并且认为这种一一对应关系是连续、稳定的。然而在生产实践中,存在着大量因切削过程中控制参数的连续变化而引起的切削突变现象,如排屑角突变、切屑螺距突变等。这与上述假定相矛盾,然而这些现象却在实验中被反复观察到。
师汉民等在低速刨削实验时发现:当切削厚度ac从0逐渐增大到0.127mm的时候,排屑角φ从39o突变到60o,主切削力增大约1倍;当切削厚度由最大厚度慢慢减少到0.07mm的时候,排屑角φ从54o突变到21o,此时主切削力降低了75%[2]。
这种切削过程中的非线性特征使关于控制参数控制方法失效,特别对高速切削和 CIM 环境的切削在线控制造成很大的困难,对切削功率及工艺效果的影响不容忽视[3]。因此,以突变理论为数学理论基础,建立完整、准确的分析模型,并对该现象进行精确地预测,不仅对通过控制参数的相关优化来改善切削条件等方法有着重要意义,也可籍此进一步推动切削基础理论的进一步发展。
1.2国内外研究现状
1.2.1突变理论简介
在自然界和人类社会活动中,除了渐变的和连续光滑的变化现象外,还存在着大量的突然变化和跃迁现象,如岩石的破裂、桥梁的崩塌、细胞的分裂等[4]。
用数学的方法来分析这些突然变化和跃迁现象的有效工具之一是突变理论。它认为所有状态分为两种:一种是稳定态,另一种是非稳定态。稳定态是指,系统在非常小的扰动下,其状态仍然能够维持不变;非稳定态是指,即使在非常小的扰动下,系统的状态也立刻发生改变。对于处于非稳定态的非线性系统,从一个平衡状态转化为另一个平衡状态,是以突变的形式发生的[4]。
考虑一个具有结构稳定性的系统,系统的势能可由势函数表示,例如在力学中势函数是系统的总能量[5],在经济学中可以是消费函数[6],在金属切削中可以是切削功率[7]等。无论在什么时候,具有结构稳定性的系统的状态都可由给定个状态变量的值来确定,且个控制参数可以对该系统的状态进行控制。René Thom用拓扑学证明了势函数的种类由控制参数的个数决定,并且认为控制参数和状态变量的个数限定在一定范围时,突变的种类仅有7种,这7种突变被称为初等突变[4],具体见表1.2-1。
表1.2-1 基本突变类型
突变类型 | 势函数 | 控制参数个数 | 状态变量 个数 |
折叠型 | 1 | 1 | |
尖点型 | 2 | 1 | |
燕尾型 | 3 | 1 | |
蝴蝶型 | 4 | 1 | |
双曲脐型 | 3 | 2 | |
椭圆脐型 | 3 | 2 | |
抛物脐型 | 4 | 2 |
在上述7种基本突变类型中,尖点型相对其他型而言比较容易创立,故接下来以尖点型突变为例子,来简要介绍突变理论的一些基本概念。
尖点突变模型势函数的一般表达式(即普适开折)为:
式中,为状态变量,、为控制参数。
平衡位置为系统理论上可能达到的状态,位于势函数的极小值,所以此时有:
即:
把由式确定的平衡曲面M称为突变流形(如图1.3-1)。而平衡曲面M的临界情况由:
即:
而决定,然后把式和式的交集称为奇点集S。
最后联立式和式,消去(相当于将奇点集S投影到控制参数平面上),可得分叉集B(如图1.3-1):
实际上,平衡曲面M定义为势函数对状态变量一阶导为零的集合,分叉集B定义为势函数对状态变量一阶导为零的集合和二阶导为零的集合的交集。
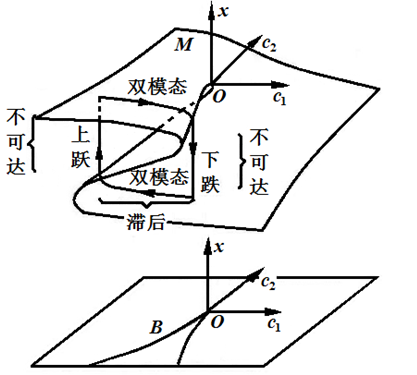
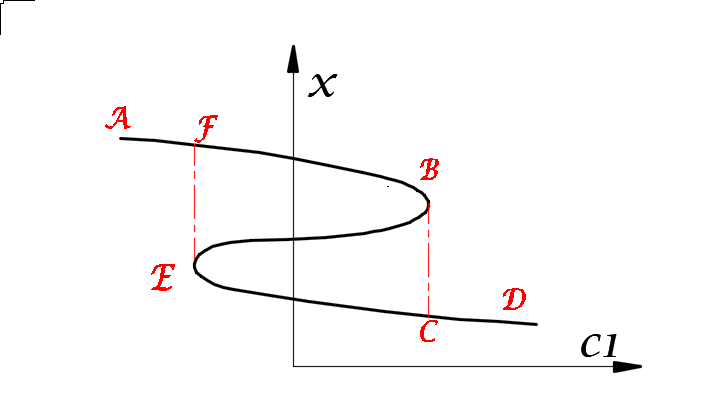
图1.3-1 尖点突变的平衡曲面与分叉集 图1.3-2 尖点突变的示意图
由图1.3-1可以知道,尖点突变流形(即平衡曲面M)呈现出折叠的形态,事实上,只有平衡曲面出现折叠,突变才有可能发生。平衡曲面的折叠使其出现了上、中、下三叶,代表了理论上可能的三种平衡位置,其中上、下两叶是稳定的,中叶是不稳定的。
通过对突变流形的分析,可得突变模型如下特性,它们也可以用作突变特征[4]:
(1)多模态:控制参数在某些范围时,系统的势能可能出现两个或多个极小值。对于尖点突变模型即双模态;
(2)突跳:当控制参数连续变化并从特定方向通过分叉集时,系统的状态会发生上跃或下跌。以图1.3-2为例,保持控制参数c2为常数:若沿路径A到D增大控制参数C1,状态变量在B点附近跌落至C点,即发生了突变;类似的,沿路径D到A减小C1,x在E点附近上跃至F点;
(3)滞后性:同样以图1.3-2为例:当控制参数x分别沿着A到D和D到A的路径变化时,根据以上分析,状态变量分别在B、E点发生突变,显然E点处C1的值小于B点处C1的值。
1.2.2突变理论的应用
突变理论虽然是一门“年轻”的理论,但在很多领域已经取得了丰硕的成果。例如找到了光的焦散面的全部可能的形式[8]。与其他的数学方法相比,突变理论在解释生物学和社会学中许多现象具有一定的优势。例如对捕食者-被捕食者系统中的群体消长情况,与微分方程相比,突变理论的预测能与实验很好的相符[4]。
在摩擦研究中,鲍久圣用突变理论建立摩擦突变的尖点模型,对提升机紧急制动过程中闸瓦“摩擦突变”现象进行了定性描述和定量预测[10]。MARCO等应用突变理论对带柔性转轴的平面运动系统的稳定性进行分析,发现系统在运动过程中不仅可能发生折叠突变,而且可能发生尖点突变或蝴蝶型突变,通过分叉集划分出不会发生突变的稳定工作区域和会发生突变的不稳定区域,提高了保障系统运行的稳定性,且理论预测值跟实际测量得到的值误差在9%以内[11]。
1.2.3排屑角预测研究现状
一直以来,国内外对于排屑角进行了大量的研究,其中许多都是通过对实验数据的分析来对其进行预测。
G.V.Stabler在刨床和车床上对不同材料的工件进行了大量单刃斜角自由切削的实验,给出了刃倾角和自然排屑角的一个简单的经验关系[11],即:
其中,值在0.9到1.0之间,随工件材料和切削条件变化。
实际上,许多学者认为排屑角不仅仅与刃倾角有关, Brown 和 Armarego等认为排屑方向应与前刀面上的摩擦方向相一致[13],即:
式中,是在前刀面上平行于切削刃的切削分力,是前刀面上垂直于切削刃的切削分力,这也是师汉民等在外圆车削实验中所采用的测量方法之一[2]。
国内学者张维纪等人认为,刀具的结构参数和加工条件也会影响排屑角 [14],通过理论分析,给出了排屑角计算公式:
其中,为平均摩擦角。
刘旺玉等人对刃倾角大于50o的斜角切削的切屑流动方向进行实验研究,通过高速钢刀具切削低碳钢(Q235)工件的实验,拟合出了排屑角的经验公式[15]:
可以看到,虽然国内外学者给出了很多的排屑角预测公式,这些研究都是侧重于某一因素或者仅仅只是给出了一个经验公式。一般情况下,大多仍然采用的是G.V.Stabler给出的著名公式—— 。
1.2.4切削模型研究现状
剪切区是一个非常窄的区域,并且有很高的剪应变率(可达 104~106s-1)[8]。由于切削过程受到很多因素的影响,虽然有很多理论建立了相关的切削模型,但通常难以建立与实际剪切变形区完全一致的切削模型。在建立模型时,大都主要考虑第一变形区的剪切变形,实现一定程度上的对实际切削过程的模拟与预测。以下介绍三种比较常见的切削模型。
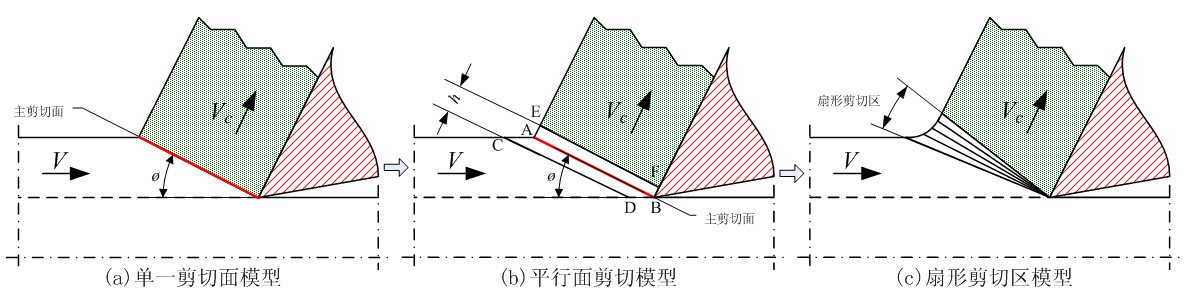
图1.3-3 主剪切区的简化模型
(1):剪切平面模型
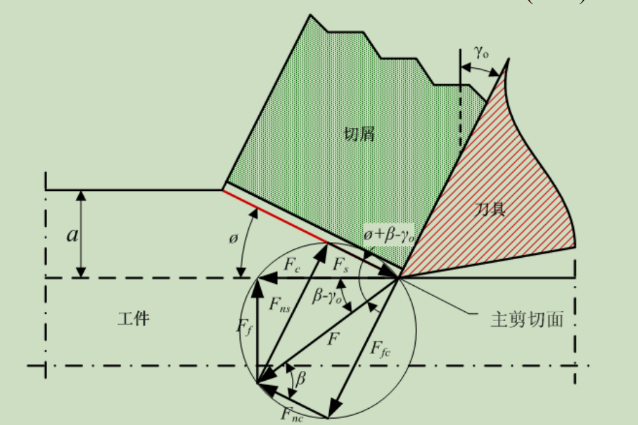
Merchant 假设材料为理想塑性体,将第一变形区视作单一剪切平面(如图1.3-3),剪应力为不随正应力变化的定值[16],这也是师汉民[2]在研究直排屑突变采用的模型。由于该模型忽略了没有考虑材料的加工硬化、忽略了剪切角和切削速度引起的剪切应力的变化等,所以其模型的预测的范围具有相当的局限性,对复杂情况的预测精度较低。
(2):等分剪切面模型
Oxley认为主剪切面 AB 平行于始剪切线 CD 和终剪切线 EF,并且平分剪切区(如图1.3-3)[17]。理论上,该模型比剪切平面模型更符合实际的情况,但是由于利用该模型提出的算法存在不收敛等问题,还需要进一步改进算法[18]。
(3):不等分剪切面模型
以上是毕业论文大纲或资料介绍,该课题完整毕业论文、开题报告、任务书、程序设计、图纸设计等资料请添加微信获取,微信号:bysjorg。
相关图片展示:
课题毕业论文、开题报告、任务书、外文翻译、程序设计、图纸设计等资料可联系客服协助查找。



