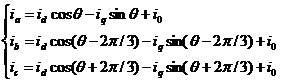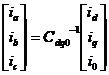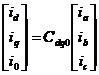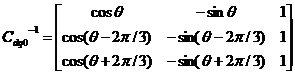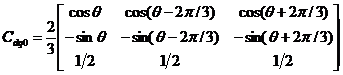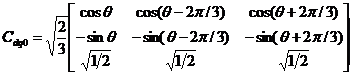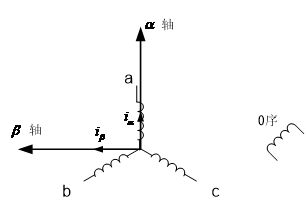IPMSM逆变器死区在线补偿策略研究毕业论文
2020-04-08 14:27:48
摘 要
本文提出了一种用于永磁同步电机(IPMSM)自适应死区补偿的矢量控制系统(该系统由可获得基波相位电压的逆变器进行供电)。为补偿因逆变器的不稳定性(空载时间、设备开关)及二极管导通电压引起的干扰电压,将DTCV(死区时间补偿电压)在转子坐标中转换为q轴DTCV。本文研究了q轴DTCV和DTCT(死区时间补偿时间)的关系。干扰电压的监测器可使用q轴的干扰电压对DTCT来进行识别。与此同时DTCV的幅值可根据检测到的DTCT从而来自适应地进行确定。DTCT的精度则是由计算确认的理想条件下有效功率和实际条件下功率的MAPE(绝对平均百分误差)来确定的。自适应的DTCT相比固定的DTCT要小,同时其MAPE在任何情况任何时间都可以控制在5%以内。
关键词:
永磁同步电机,死区时间补偿时间,死区时间补偿电压,电压源型逆变器,干扰电压
Abstract
This paper proposes a type of vector control system utilized for the adaptive dead-time compensation of IPMSM (the power of such system is supplied by the inverter that is able to obtain fundamental wave phase voltage). To compensate the disturbance voltage caused by the instability of the inverter (non-loading time and equipment switch) as well as the diode conduction voltage, dead-time compensation voltage (DTCV) is converted to q-axis DTCV in the rotor coordinate. This paper researches the relation between q-axis DTCV and dead-time compensation time (DTCT). The disturbance voltage monitor is able to utilize the q-axis disturbance voltage to recognize DTCT. Simultaneously, the amplitude of DTCV is able to be determined adaptively according to the detected DTCT. The precision of DTCT is determined in accordance with the effective power under the ideal condition confirmed by calculation and the mean absolute percent error (MAPE) of the power under the actual condition. The adaptive DTCT is smaller than the fixed DTCT; simultaneously, its MAPE is able to be controlled under any circumstance at any time.
Key Words:permanent magnet synchronous motor (PMSM), dead-time compensation time (DTCT), dead-time compensation voltage (DTCV), voltage source inverter, disturbance
目 录
摘 要 I
Abstract II
第1章 绪 论 1
1.1研究目的和意义 1
1.2国内外的研究现状 1
1.3研究内容 2
第2章 永磁同步电机数学模型和矢量控制系统 3
2.1 派克变换与克拉克变换 3
2.1.1 派克变换 3
2.1.2 Clarke变换 5
2.2 永磁同步电机数学模型 7
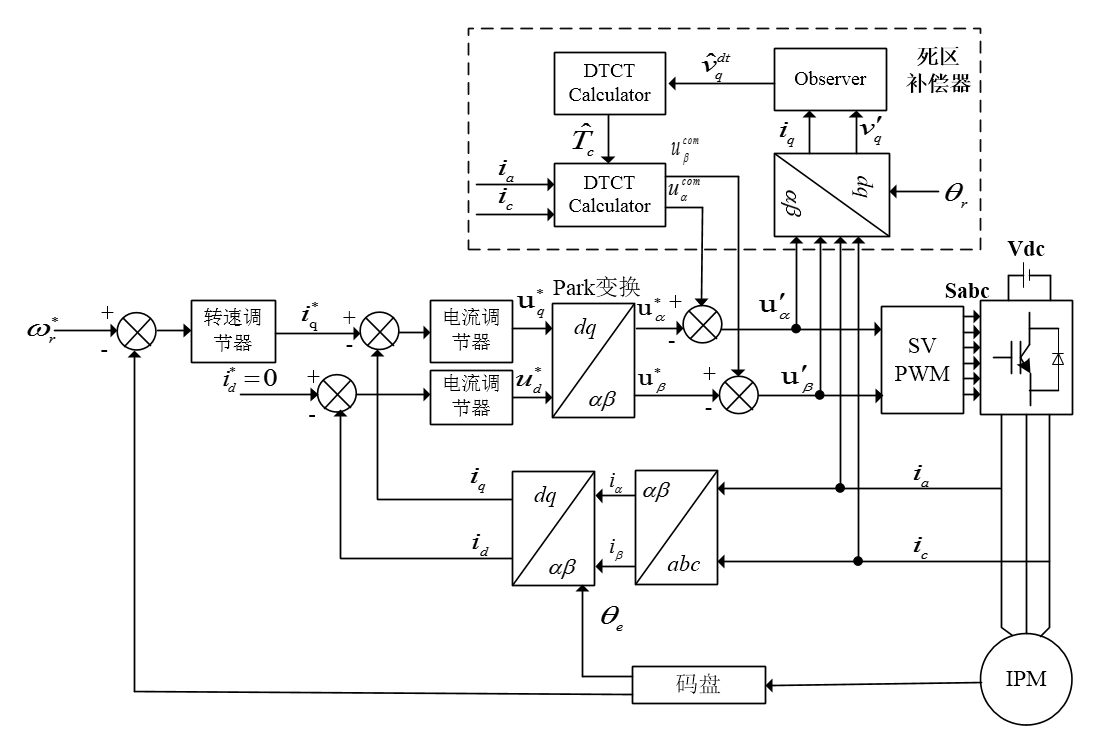
2.3矢量控制系统 9
2.4本章小结 13
第3章 逆变器死区在线补偿策略 14
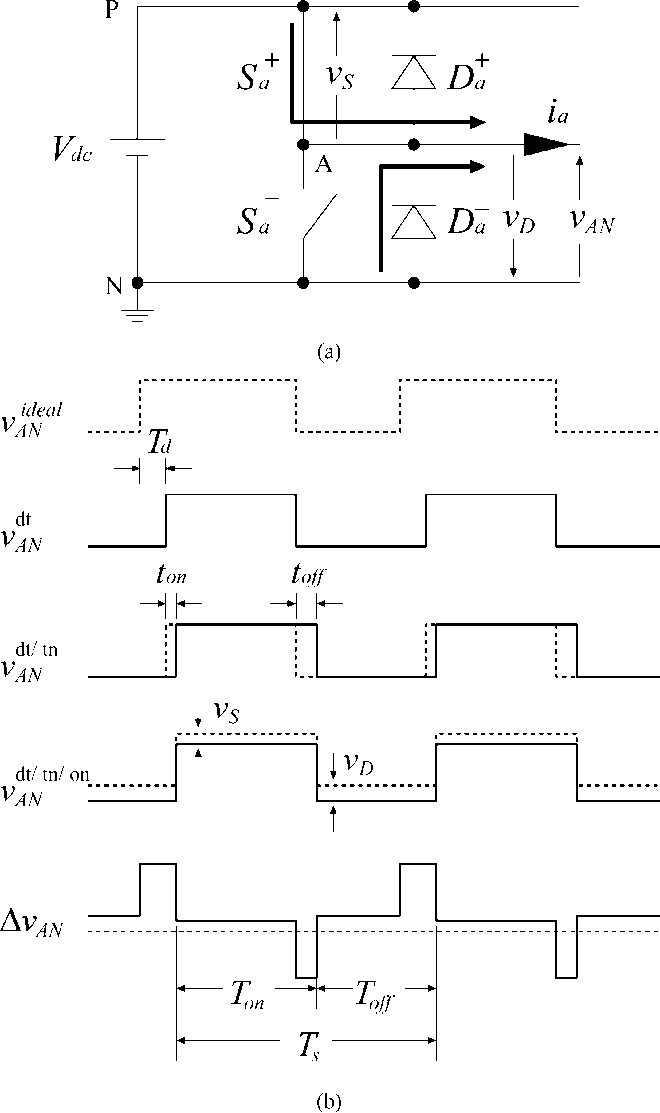
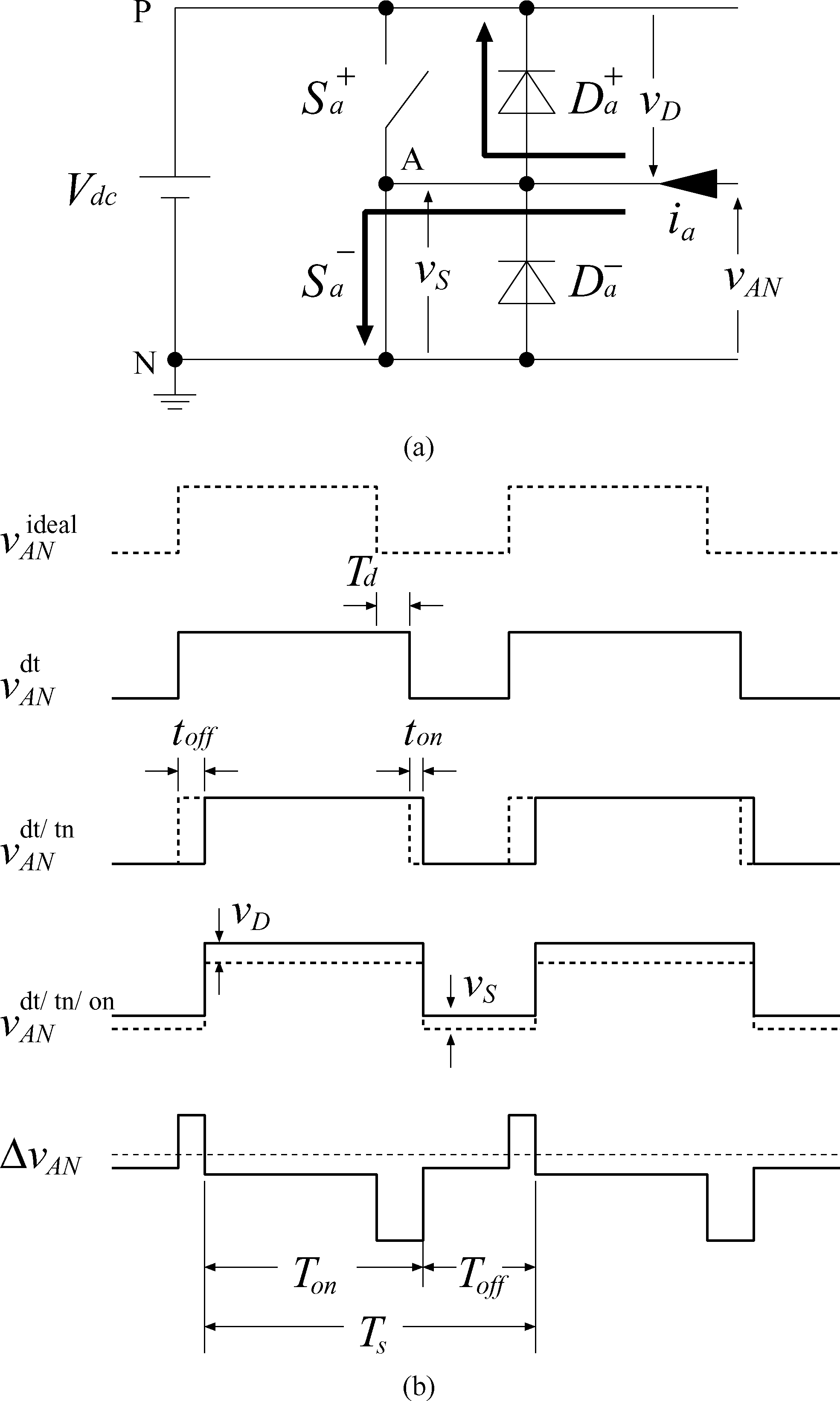
3.1死区补偿 14
3.1.1死区时间补偿电压(DTCV)的公式推导 14
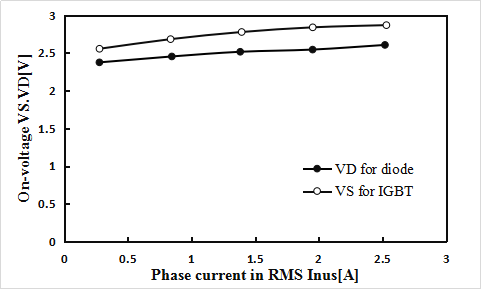
3.1.2开关和二极管的导通电压 16
3.2 死区时间补偿时间(DTCT)的在线确定 18
3.2.1 dq轴上的DTCV的确定 18
3.2.2 DTCT的确定 20
3.2.3 q轴估计干扰电压的确定 21
3.3本章小结 23
第4章 仿真结果分析 24
4.1部分元件参数的选择 24
4.2系统仿真模型搭建 26
4.3仿真结果分析 26
4.4 本章小结 30
第5章 总结与展望 31
致 谢 32
参考文献 33
附录A 35
附录B 36
附录C 37
第1章 绪 论
1.1研究目的和意义
永磁同步电机(IPMSM)具有高气隙磁通,大转矩惯性,结构紧凑,可靠性高,可控性好,功率因数高等优点,广泛用于交流伺服系统,但很多场合要求系统具有较宽的调速比,那么如何满足系统在低速情况下的性能尤为重要[1]。由于系统在低速情况下由于逆变器死区效应输出产生的相电流谐波极易造成如下状况:
1)逆变器输出波形发生畸变,并使电机端电压与逆变器参考电压存在偏差,降低伺服系统控制的精度;
2)导致零电流钳位现象,使电机输出转矩发生脉动,尤其当电机低速运行时更加严重,甚至导致系统的不稳定。
另外由于开关频率的不断提高,死区效应对逆变器输出电压和输出电流的影响也越来越严重。
因此为削弱死区效应,抑制零电流钳位现象,削弱低频电流谐波,改善电流正弦度,提高系统低速运行性能,提高IPMSM 控制性能对逆变器死区进行有效补偿是非常必要的[2]。
1.2国内外的研究现状
在过去的十年中,由电压源型逆变器供电的永磁同步电机(IPMSM)驱动器已经有过广泛的开发。也衍生出了很多应用,如需要一个基本的相电压信息的转子位无传感器驱动电机。由于逆变器输出端不能对基本相电压进行检测,因此通常使用指令电压来对实际电压进行代替。然而,由于逆变器的不稳定性如空载时间、设备开关时引起的及二极管导通电压所引起的干扰电压,指令电压常不会与基本相电压实际情况相一致,死区就对逆变器避免支路短路这一问题上起到了重要的作用。设备开关和导通时的电压在设备的实际使用中是不可避免的。为解决这一问题,一些研究人员尝试着对逆变器的不稳定性进行补偿。
死区精确补偿需2个条件:误差电压V 和电流方向正确估算。
在[3]中,死区补偿是通过引入DTCV(死区时间补偿电压)来实现的。DTCV是通过分析理想和实际情况下逆变器输出功率间的平均误差来确定的。此种方法虽然实现比较容易,但是设备开关时并不能对死区的影响来进行补偿。然而在[4]中,通过引入DTCT(死区时间补偿时间)来解决这一问题。DTCT包括了开关时间及导通电压以及死区时间。所以该方法不仅可以对死区效应进行补偿,也可以对设备开关时间以及导通电压的影响进行补偿。因DTCT通常是未知参数,所以有必要对DTCT进行识别。而在[4]中,DTCT通常由事先开发好的自适应的识别程序来识别,之后再将识别出来的DTCT应用于死区补偿。但是因DTCT随着操作点的不同会产生一定的变化,故固定的DTCT也不能做到屡试不爽[5]。所以针对该问题,已经提出了一种通过使用干扰电压监测器的永磁同步电机(IPMSM)自适应的死区时间补偿方案[6]。这种方法利用了基于永磁同步电机的理想模型而研制的干扰监测器,可以同步估算旋转参考系中的dq轴的DTCV。然后,将估测的dq轴DTCV值直接补偿到由电流控制器产生的dq轴指令电压上。由于dq轴DTCV基频是驱动频率的6倍,故随着驱动频率的增加会产生一定的延迟,有可能会导致死区补偿的衰减[7][8][9]。
本文提出一种用于永磁同步电机(IPMSM)自适应死区补偿的矢量控制系统(该系统由可获得基波相位电压的逆变器进行供电)。当d轴电流为零时,对DTCT和q轴的DTCV间的关系进行研究[10][11]。本文中,由于逆变器有不稳定性,假设q轴DTCV值等于q轴干扰电压值。该q轴干扰电压值由干扰监测器监测得到。而DTCT由估测的q轴干扰电压来进行计算[12][13]。通过利用自适应的DTCT来确定DTCV。这种方案的优点是:只对DTCV的幅值进行调整,故对干扰监测器的估测延迟影响都比较小。并且,自适应的死区时间补偿策略只对监测器有要求。模拟结果证实了文中方法的可行性和有效性[14][15]。
1.3研究内容
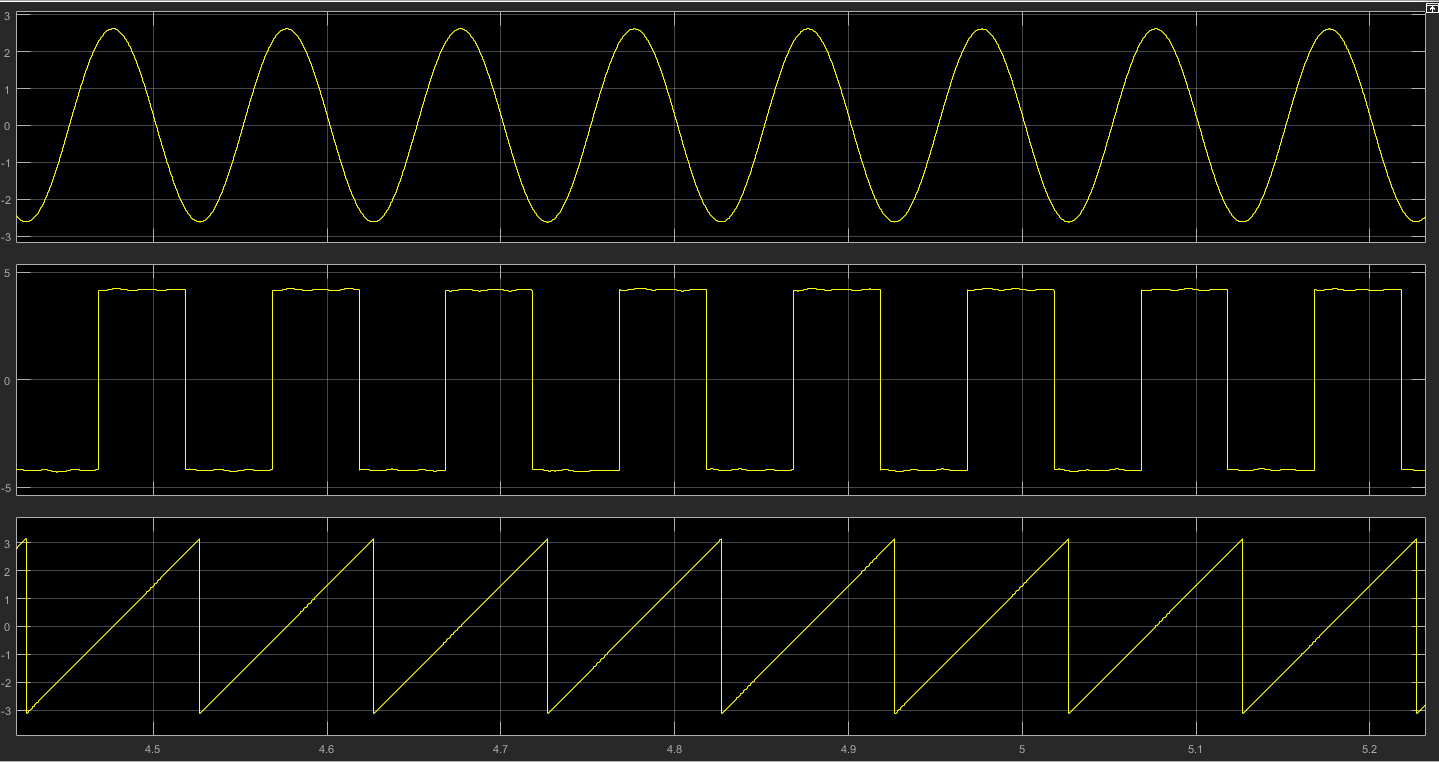
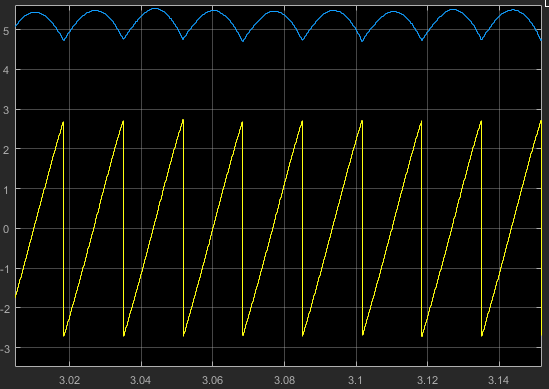
1)死区效应分析(包括死区效应对电压和电流的影响和补偿之前的相电流波形图)。
2)提出基于扰动观测器的死区补偿方法。
3)用基于扰动观测器的死区补偿方法进行死区补偿(得出补偿之后的电流波形)。
4)比较补偿前后相电流的波形图,并对所提出的死区补偿方法进行验证。
第2章 永磁同步电机数学模型和矢量控制系统
2.1 派克变换与克拉克变换
2.1.1 派克变换
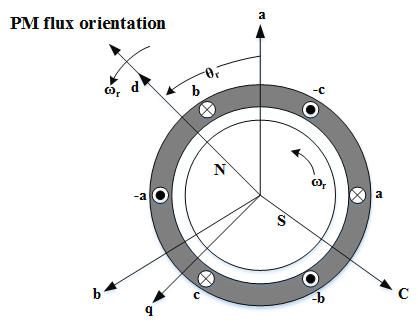
图1所示为本文对于坐标轴的定义。abc轴定义成每相电流磁通量的方向。d轴则定义成永磁体磁通量方向。q轴定义成向前90°步进的方向。dq轴和永磁同步电机的转子同步。
图2.1 坐标轴定义
派克变换(C2S/2R)是现在占主流地位的交流电机分析计算时的基本变换。park转换,也称派克变换,英文为Park transformation,为现在占主流地位的交流电机分析计算时的基本变换。在电力系统分析和计算中,park转换具有重要的理论和实际意义。
从数学意义上讲,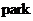 变换不存在任何问题,仅仅为一个坐标转换罢了。自
变换不存在任何问题,仅仅为一个坐标转换罢了。自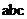 坐标转换为
坐标转换为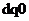 坐标,
坐标,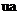 ,
,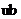 ,
,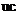 ,
,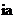 ,
,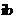 ,
,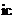 ,
,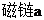 ,
,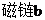 ,
,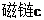 ,上述参数均可以转变至
,上述参数均可以转变至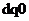 坐标里面,假如存在需要,仍能够逆变回去。
坐标里面,假如存在需要,仍能够逆变回去。
由物理意义来说,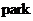 变换即为把
变换即为把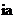 ,
,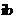 ,
,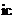 ,电流在α、β轴上的投影,等价至d,q轴上,把定子中的电流均等价至直轴与交轴中。针对稳态而言,经过这样的等价之后,
,电流在α、β轴上的投影,等价至d,q轴上,把定子中的电流均等价至直轴与交轴中。针对稳态而言,经过这样的等价之后,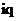 ,
,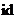 刚好即为一个常量。
刚好即为一个常量。
自观察人员的视角来讲,我们的观察点已然自定子转换至转子中,我们不再注重由定子三个绕组形成的旋转磁场,但是关注如此等价之后的由直轴与交轴形成的旋转磁场。如此做导致在建立转子回路电磁关系的微分方程时,它的系数矩阵变成了常量矩阵,并非伴随时间与空间量而改变的系数矩阵。如此在很大程度上简化了剖析发电机、电动机的电磁关系的微分方程。
匀速圆周转动的状况下,派克变换即为经过相应的角度旋转变换,将旋转里面的向量变成静止直角坐标系中的量,也就是把空间静止坐标系取代旋转坐标系。
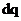 变换为一种解耦控制形式,其把异步电动机的三相绕组转变成等价的二相绕组,而且将旋转坐标系转变为正交的静止坐标,就能够获取采用直流量来表达电压及电流的关系式。
变换为一种解耦控制形式,其把异步电动机的三相绕组转变成等价的二相绕组,而且将旋转坐标系转变为正交的静止坐标,就能够获取采用直流量来表达电压及电流的关系式。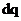 变换让每个控制量能够依次进行控制,能够消去谐波电压与不对称电压的影响,因为运用了同步旋转坐标转变,轻易就可以达到基波和谐波的分离。
变换让每个控制量能够依次进行控制,能够消去谐波电压与不对称电压的影响,因为运用了同步旋转坐标转变,轻易就可以达到基波和谐波的分离。
Park转变是将交流坐标系转变成直流坐标系,通常在VSC(voltage source converter)的操控之中会常常用到,它把交流转变的因数转变为直流坐标系中,安稳的时候dq量能够维持不变。VSC操控就是操控已经转变过的dq量进而对体系的电压与电流等数据展开操控的。
用定子电流来举例子。假如定子三相绕组里面的电流分别是ia,ib,ic,并且转子d轴和定子a相绕组轴线组成的角度是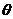 (电角),dq0转变以后定子所具有电流的dq0分量各自是id,iq,i0。将旋转的d、q轴中的id,iq都平移到定子a、b、c三相轴线中,然后结合零序电流i0,就能获得出ia,ib,ic:
(电角),dq0转变以后定子所具有电流的dq0分量各自是id,iq,i0。将旋转的d、q轴中的id,iq都平移到定子a、b、c三相轴线中,然后结合零序电流i0,就能获得出ia,ib,ic:
(2.2)
式2.2中,
(2.3)
(2.4)
式(2.1)-式(2.4)中,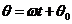 ,
,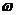 为转子的角速度;
为转子的角速度;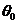 为0时刻时,d轴与a轴夹角;转子转动的时候,Cdq0会形成一个时变阵。假如
为0时刻时,d轴与a轴夹角;转子转动的时候,Cdq0会形成一个时变阵。假如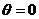 ,就是转子不会移动,并且d轴和a轴重叠的时候,dq0坐标系化简成αβ0坐标系。
,就是转子不会移动,并且d轴和a轴重叠的时候,dq0坐标系化简成αβ0坐标系。
很明显,式2.4不符合正交矩阵的条件,上面所说的是转变为同数额的转变,将转变矩阵单位正交化形成正交矩阵
(2.5)
就是Cdq0-1= Cdq0T ,这个时候转变会变成为形同功率的转变。
2.1.2 Clarke变换
Clarke(克拉克)变换也就是C2S/2R转变,它转变以后的量依旧属于交流量,并且它的数额是伴随abc三相数额的转变而不同的。它的通常用于随时无功功率操控
αβ0坐标系是一种两相类型的坐标系,并且α轴和a围绕组轴线重叠,β轴大于α轴有90°电角,0序属于一个单独的体系。
用电流来举例子,反映出abc和αβ0坐标系相互的坐标转变。将图中α和β轴线里的电流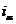 和
和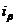 都平移到a、b、c三相轴线中,接着结合单独的零序电流
都平移到a、b、c三相轴线中,接着结合单独的零序电流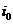 ,就能够获得
,就能够获得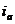 、
、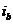 和
和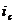 :
:
以上是毕业论文大纲或资料介绍,该课题完整毕业论文、开题报告、任务书、程序设计、图纸设计等资料请添加微信获取,微信号:bysjorg。
相关图片展示:
课题毕业论文、开题报告、任务书、外文翻译、程序设计、图纸设计等资料可联系客服协助查找。