时间序列模型在股票市场收益率的预测的应用毕业论文
2020-04-09 14:04:06
摘 要
股票市场自诞生到发展已经经过了很多年的历史,对于全球经济发展以及企业发展等方面都具有很重要的意义。全球股市每天都有着成千上万笔交易,股票已成为人们生活中不可缺少的一部分。研究股票价格的变化趋势可以帮助人们更加了解股票市场,完成更有效的投资从而获得更高的回报。
本文首先介绍了时间序列分析中的一些基本概念,如平稳性、纯随机性、自相关函数以及偏相关函数,以及时间序列中基本的两个模型——自回归移动平均(ARMA)模型、广义自回归条件异方差(GARCH)模型的相关概念,为建立股票价格趋势预测模型作铺垫。然后,以2016至2017年间的上证综合指数数据为例,分别对上证综合指数的日收盘价序列以及5日移动平均价格序列建立ARIMA模型。建模的步骤主要为数据的预处理、模型阶数的确定、模型的参数估计、模型的显著性检验、参数的显著性检验。得到模型后,用建得的模型分别对序列进行拟合与预测。结果表明模型对数据拟合结果较好,日收盘价序列未来呈一种略微上升的趋势,5日均线序列呈一种较平缓的略微上升的趋势。最后,使用GARCH模型对上证综合指数日收盘价序列ARIMA模型的残差序列进行拟合,并对日收盘价ARIMA模型的残差序列进行了拟合及预测。
关键词:ARIMA模型;GARCH模型;上证综合指数;预测
Abstract
The Stock Market has developed for a long period of time, and it is of great significance to the development of global economic and enterprises. There are thousands of transactions around the world every day, and stocks have become an indispensable part of people's lives. Studying the trend of stock prices will help people understand the stock market more effectively and complete more effective investment to obtain higher returns.
At first, some basic concepts in time series analysis are introduced, such as stationarity, pure randomness, autocorrelation function, and partial correlation function. Besides, two basic models in the time series are also introduced: the concept of autoregressive moving average (ARMA) model and generalized autoregressive conditional heteroskedasticity (GARCH) model, which pave the way for the establishment of a stock price trend forecasting model. Then, taking the Shanghai Composite Index data from 2016 to 2017 as an example, the ARIMA model was established for the daily closing price sequence of the Shanghai Composite Index and the 5-day moving average price separately. The steps of modeling are mainly data preprocessing, model order determination, model parameter estimation, model significance test, and parameter significance test. After the model was obtained, the constructed model was used to fit and predict the sequence. The results show that the model fits the data well, and the daily closing price series shows a slight upward trend in the future, and the 5-day moving average sequence shows a slightly flat increasing trend. Finally, using the GARCH model to fit the residual series of the ARIMA model of the daily closing price sequence of the Shanghai Composite Index, and fitting and forecasting the residual series of the daily closing price ARIMA model.
Key Words: ARIMA; GARCH; Shanghai Composite Index; Forecast
目 录
第1章 绪论 1
1.1 研究背景、目的及意义 1
1.2 国内外研究现状 2
1.3 研究内容及目标 2
第2章 时间序列模型简介 4
2.1 基本概念 4
2.1.1 平稳性 4
2.1.2 纯随机性 4
2.1.3 自相关函数 4
2.1.4 偏相关函数 5
2.2 自回归移动平均(ARMA)模型 5
2.2.1 自回归(AR)模型 6
2.2.2 移动平均(MA)模型 6
2.2.3 自回归移动平均(ARMA)模型 7
2.3 条件异方差模型 7
2.3.1 自回归条件异方差(ARCH)模型 8
2.3.2 广义自回归条件异方差(GARCH)模型 8
第3章 股票价格预测的实证分析 9
3.1 数据的选择与预处理 9
3.1.1 描述性统计 10
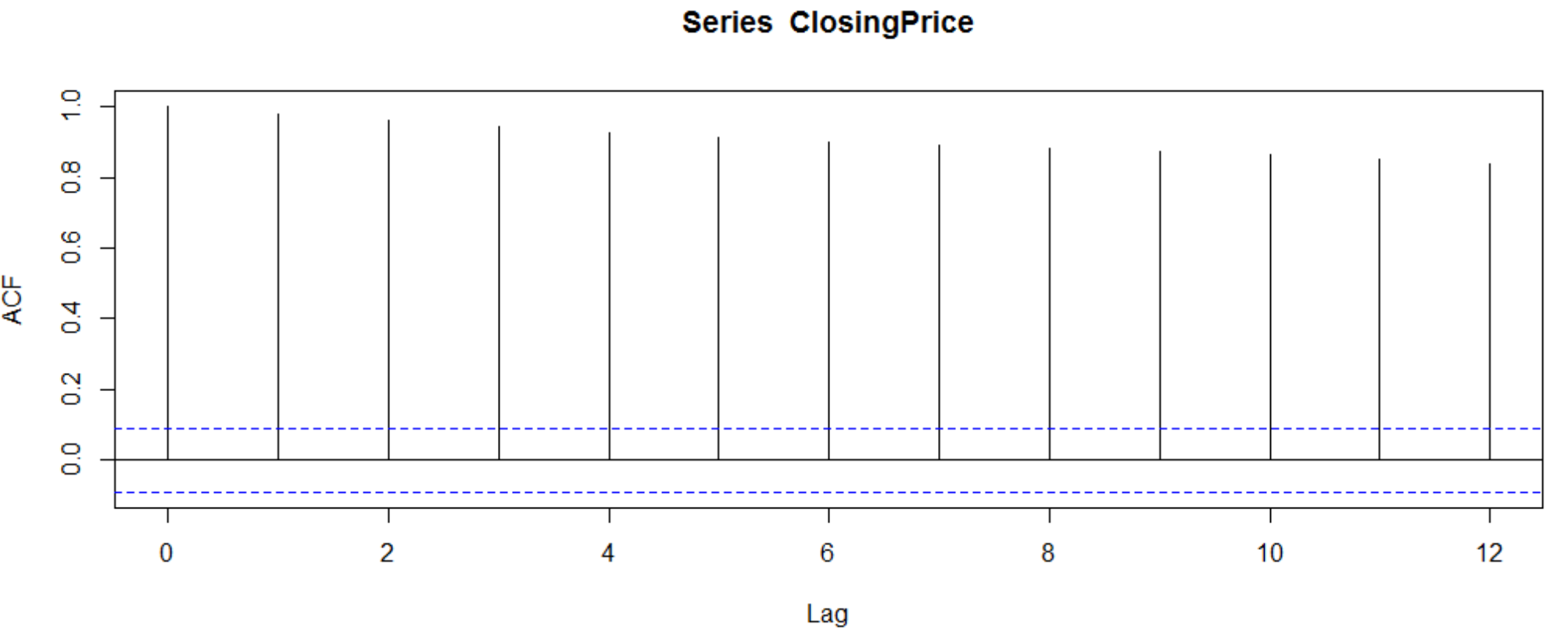
3.1.2 平稳性的判断 10
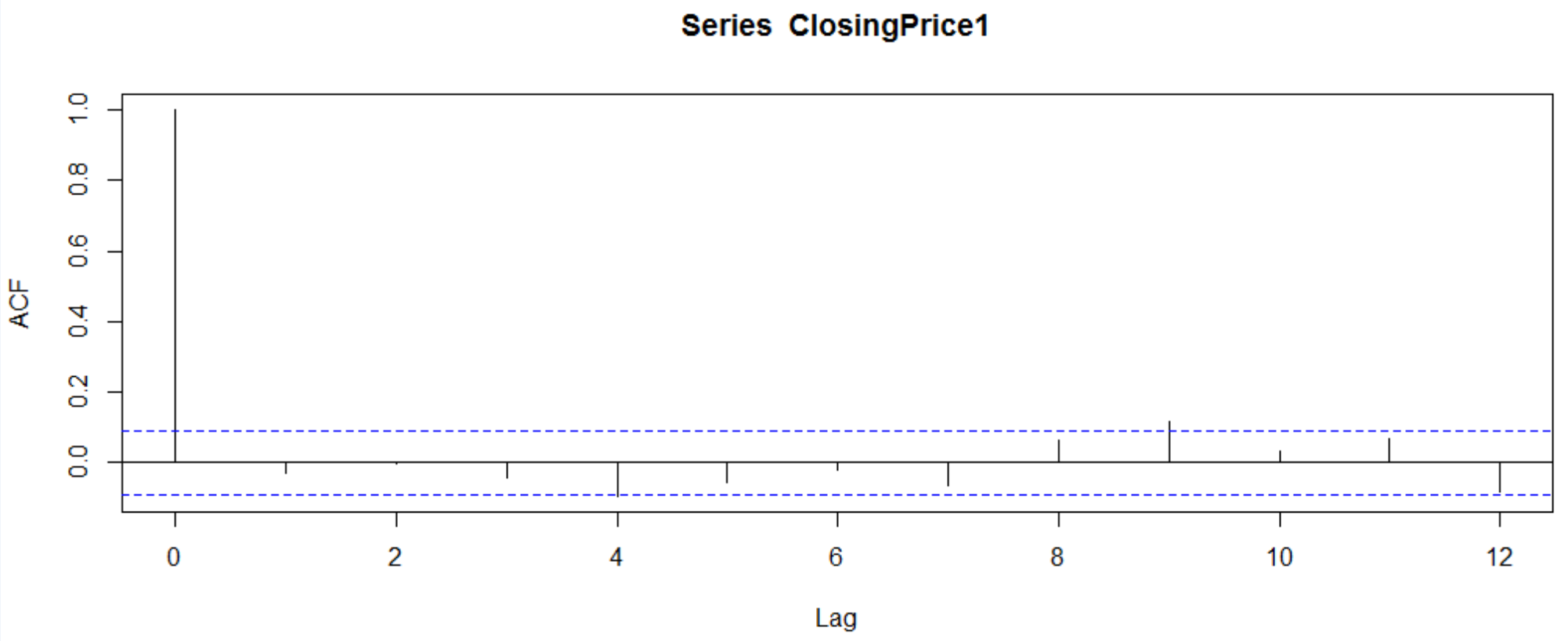
3.1.3 纯随机性的判断 12
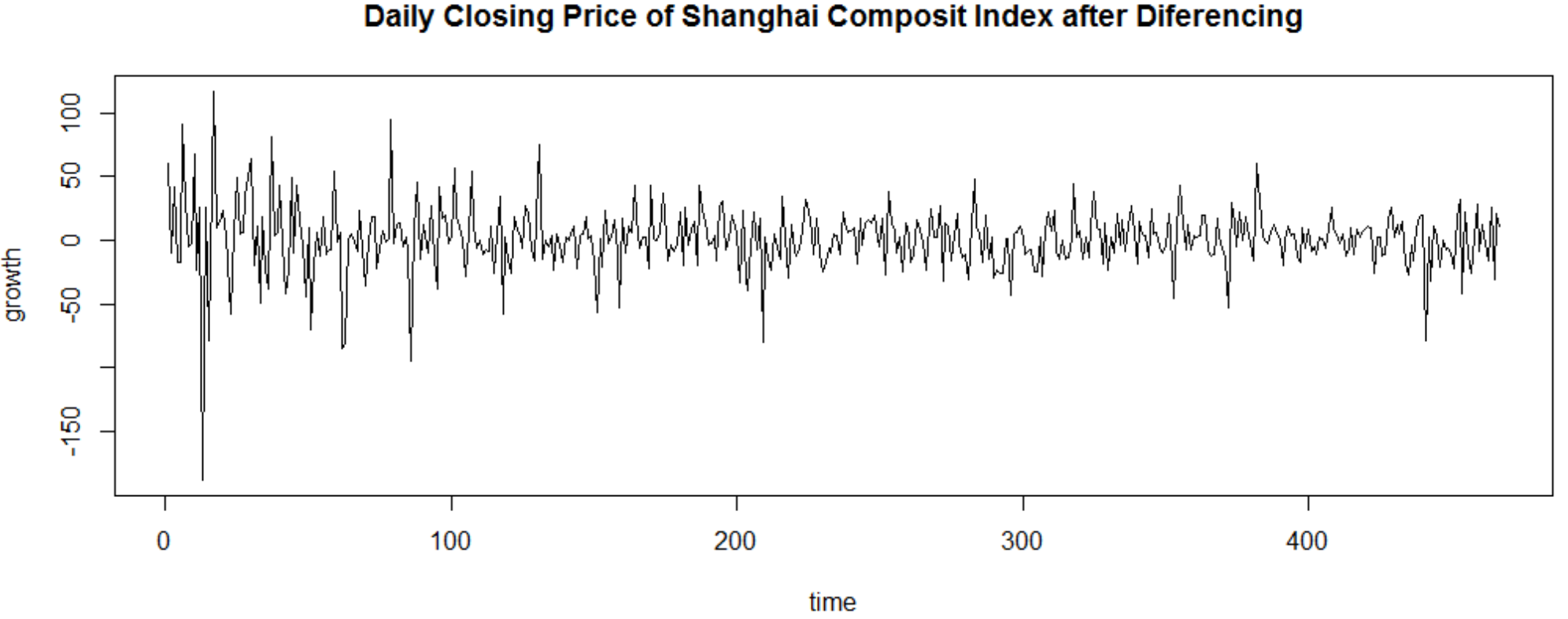
3.1.4 序列的平稳化处理 12
3.2 模型的建立 13
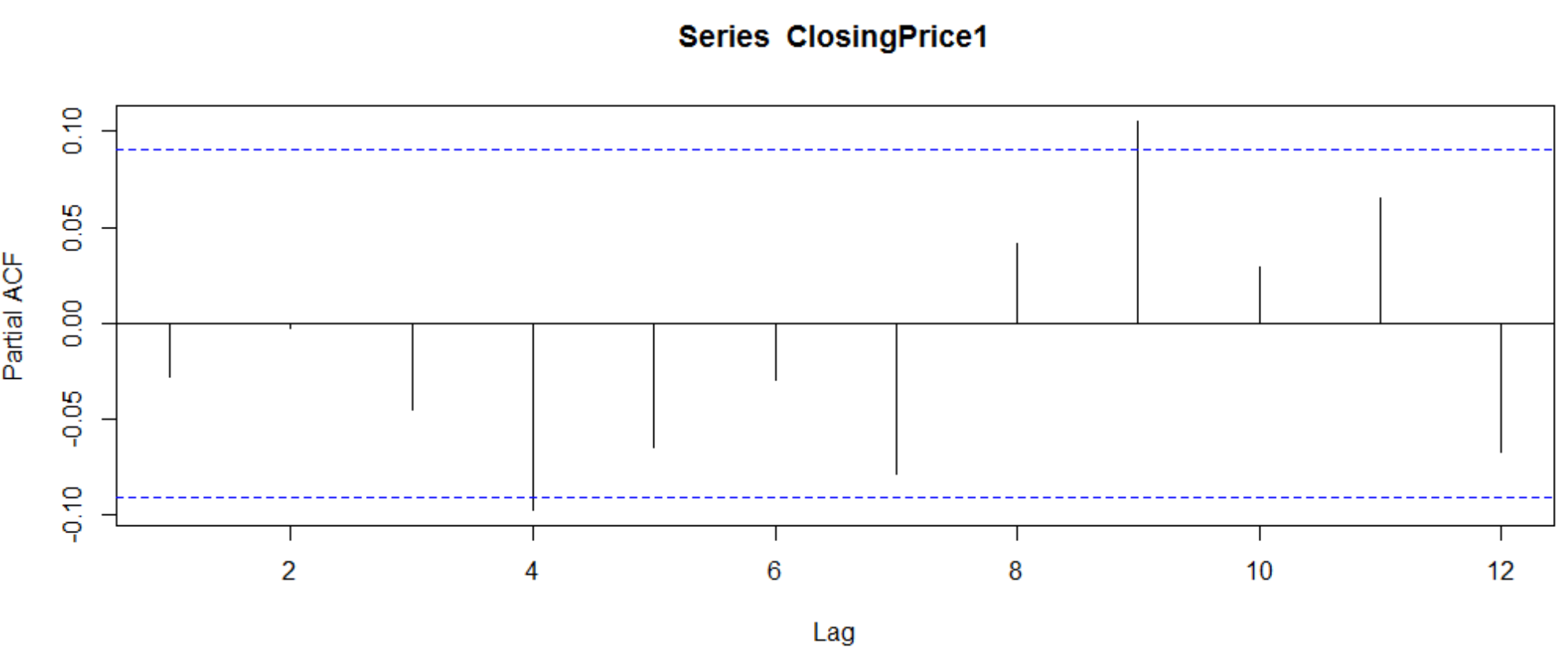
3.2.1 模型阶数的确定 14
3.2.2 模型的参数估计 15
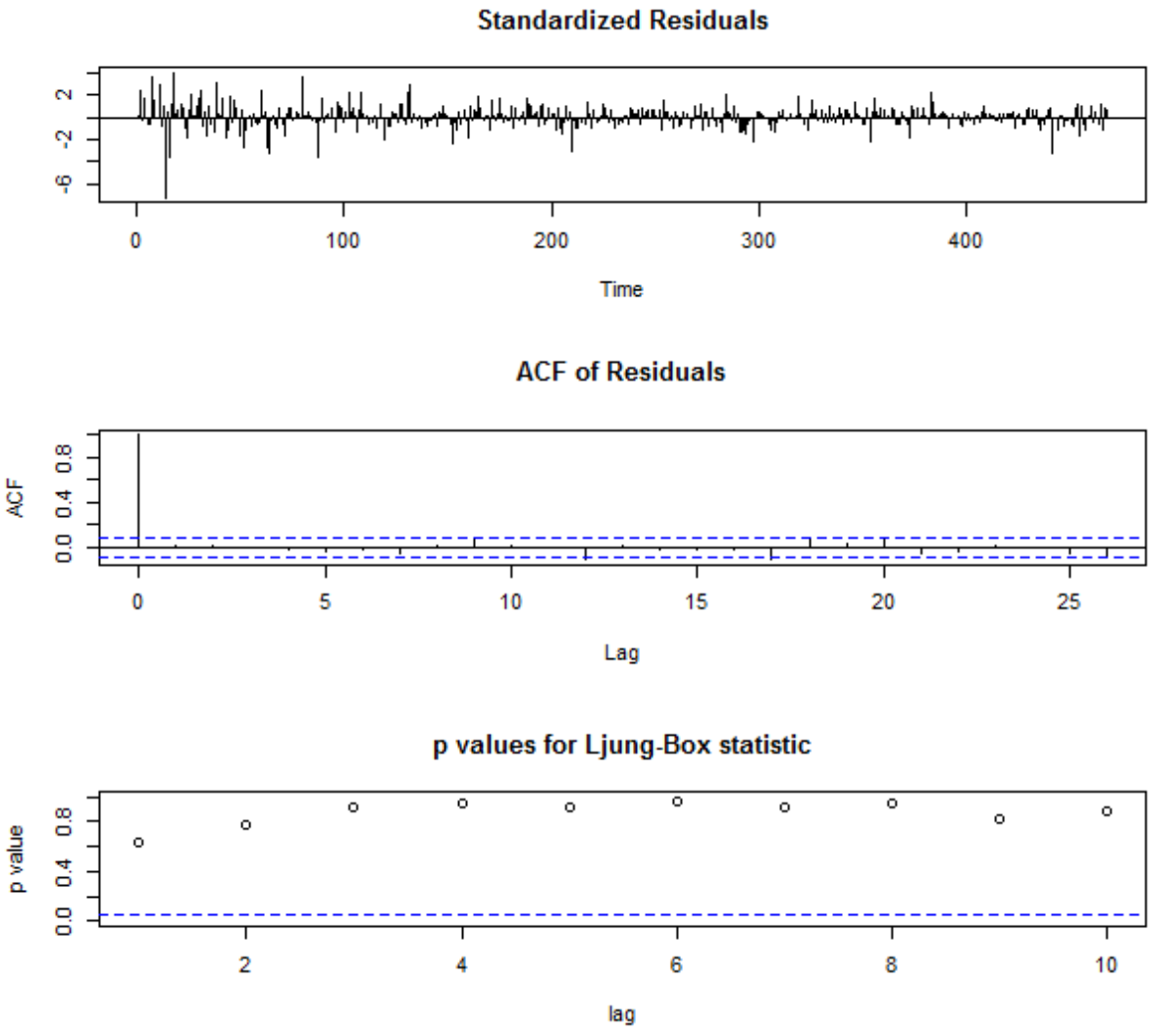
3.3 模型的检验 16
3.3.1 模型的显著性检验 16
3.3.2 参数的显著性检验 17
3.4 模型的预测 18
第4章 股票均线预测的实证分析 19
4.1 数据的预处理 19
4.1.1 描述性统计分析 19
4.1.2 平稳性检验 20
4.1.3 纯随机性检验 21
4.1.4 序列的平稳化处理 21
4.2 模型的建立 22
4.2.1 模型的定阶 23
4.2.2 模型的参数估计 24
4.3 ARMA模型的检验 24
4.3.1 模型的显著性检验 24
4.3.2 参数的显著性检验 25
4.4 样本的预测 26
第5章 GARCH模型在拟合股票价格模型残差项中的应用 27
5.1 股票价格模型异方差检验 27
5.2 模型的建立 28
5.3 模型的检验 29
5.4 模型的预测 30
第6章 结论 31
参考文献 32
致谢 33
第1章 绪论
1.1 研究背景、目的及意义
随着社会的不断发展,人们的经济条件有了很大的提高,越来越多的人开始对金融市场予以关注甚至投身于金融市场以实现资本的壮大。在庞大的金融市场中,股票市场是其一个非常重要的组成部分。股票作为一种有价证券,通过一定的机制改变着人们的资本分配。而站在股票从业者的角度,以为股票市场的诸多不确定因素,人们可以通过买卖股票获得极为可观的收入,也可能输光持有的资本。全球各地都遍布着亿万股民,股市每天都在进行着成千上万笔交易,其交易量极其庞大。伴随着互联网行业和金融行业的持续发展与扩张,股市还将越来越多地侵入并改变人们的生活,股民数量将持续增加。但是由于股票市场规模的扩张以及股民的增加,随之而来的问题就是股票将更大程度上影响着人们乃至众多家庭的生活,股票市场中的小波动都将给社会的经济分配带来重大的改变。这是因为股市价格波动的不确定性经常让股民无法把握,而此时如果股民们缺乏足够的自身数学金融分析能力或者专家指导,同时又手持众多资本并急于进行成功的投资,那么很有可能做出不理智的行为。而做出不理智的行为归根结底是对股票价格的判断产生了失误。只要对价格趋势的把握程度提高,股民将获得丰厚的资本回报。因此预测股票的价格趋势显得尤为必要。
股票市场是国民经济的重要组成部分,而且股票市场的发展对国民经济的发展起着重要的推动作用。股票市场同时还受到国民经济发展形势的制约。中国的股票市场建立的比较晚,虽然股市自建立起到现在不断地发展进步并且持续健壮,但市场表现出的价格波动幅度和风险性仍要大大高于国外成熟的股票市场[1]。因此,想在中国股票市场中进行合理的资本投资,更加有必要在对股票的价格趋势上进行深入的研究工作。对股票市场的研究工作有很多,同时研究人员也很多,而我们只对其中一小部分进行研究,本文将研究的重点就是股票价格趋势的预测。预测股票的走势一直是人们尤其是股票从业者最关心的问题,而时间序列模型在股票相关研究工作的发展中成为了预测股票市场的一个非常重要的工具。可以想象,当股票的价格趋势可以通过合理的数学模型来分析、预测之后,股民们投资时将会对股票的风险性、收益率有更多的了解,进而对待选择投资的对象有更好的把握并进行相对较高资本回报的股票投资。此外,除了对股民有莫大的帮助,站在国家层面上看,研究股票的价格趋势还能促进国家经济的发展。
目前进行股票价格趋势研究的学者们大多数希望通过调整和完善已有的预测模型来得到更优的预测结果。现有的对股票市场价格的研究大体上都是从影响股票价格的因素进行研究的。但是股票价格是企业在资本市场上一系列复杂活动共同作用所形成的结果,很难从某一个或几个因素对价格进行正确的分析[2]。因此,对于预测股票的价格的问题可从考虑其数据本身出发,而不是直接考虑各种因素对其的影响。利用股票价格的历史数据来研究股票价格未来变化的趋势可以分析出股票价格在时间序列上的变化规律,又可以较准确地把握随机波动的干扰性,故可较准确预测股票的价格在短期内的变化。使用时间序列模型来对股票的价格趋势进行研究,对股民们进行投资选择、股票市场的发展以及国家经济的发展等都具有实际指导的意义。如果股票价格趋势得到把握,股票市场将会越来越健壮,股民投资将会越来越理性,对经济社会乃至整个社会都将起到巨大的推动作用。
1.2国内外研究现状
股票起源于16世纪的欧洲,是伴随着股份有限公司体制的出现而诞生的,在欧美洲已有很长的发展历史。研究股票大多应用的是由 Karl Pearson(1905)[3]提出的醉汉(ARIMA)模型,该模型目前广泛应用于计量经济学领域,同时该模型也是有效市场模型的核心。此外,残差自回归模型、异方差模型、指数平滑模型、BP神经网络等时间序列模型也都在股票的预测领域有着广泛的应用。Graham和Dodd(1988) [4]曾尝试过通过观察相关的参数情况而不是预测股票的价格来帮助人们选取购入的股票;而Wadia(2010)[5]等人在研究中得到了ARIMA模型比直接预测能得到更精准的预测结果的结论;Kailash(2009)[6]分别使用了ARIMA模型、VAR模型以及VECM模型三种方法对股票价格进行了预测并做出比较;Datta(2016)[7]使用了反向传播算法的人工神经网络模型,通过NIFTY收益的波动性和黄金回报的波动性预测印度股市的波动性。
相较于国外,国内股市发展起步较晚,但近些年越来越多的学者开始重视股市行情变化,开始对这方面进行研究。冯予(1998)[8]提出使用非线性时间序列模型来对股市的历史数据进行拟合,并用门限自回归模型来消除趋势来得到平稳序列进行建模。吴世农和吴育辉(2003)[9]找出了对股票价格影响最大的三个因素——发行股票的企业及所在行业的发展前景、未来的收益和风险。丁忠明(2010)[10]提出股票每月的平均发行价格与市场指数之间有正相关关系,而与上市溢价率之间的关系是为负相关的结论。蔡玉兰(2010)[11]在固定增长股利贴现模型的基础上,结合资本资产定价模型和改进的杜邦分析法,提出了九种对股票价格会产生影响的因素,如贝塔系数、股利的发放率、无风险报酬率、市场组合的预期报酬率等。王春丽(2010)[12]通过建立面板模型探究在市净率( P/B)系数和流通股比例( CSP) 等因素共同影响下行业整体业绩增长对股票价格水平的影响。吴树畅(2011)[13]构建了动态股票价格模型,揭示了不同类型市场不同类型公司股票价格大小的驱动因素。
1.3研究内容及目标
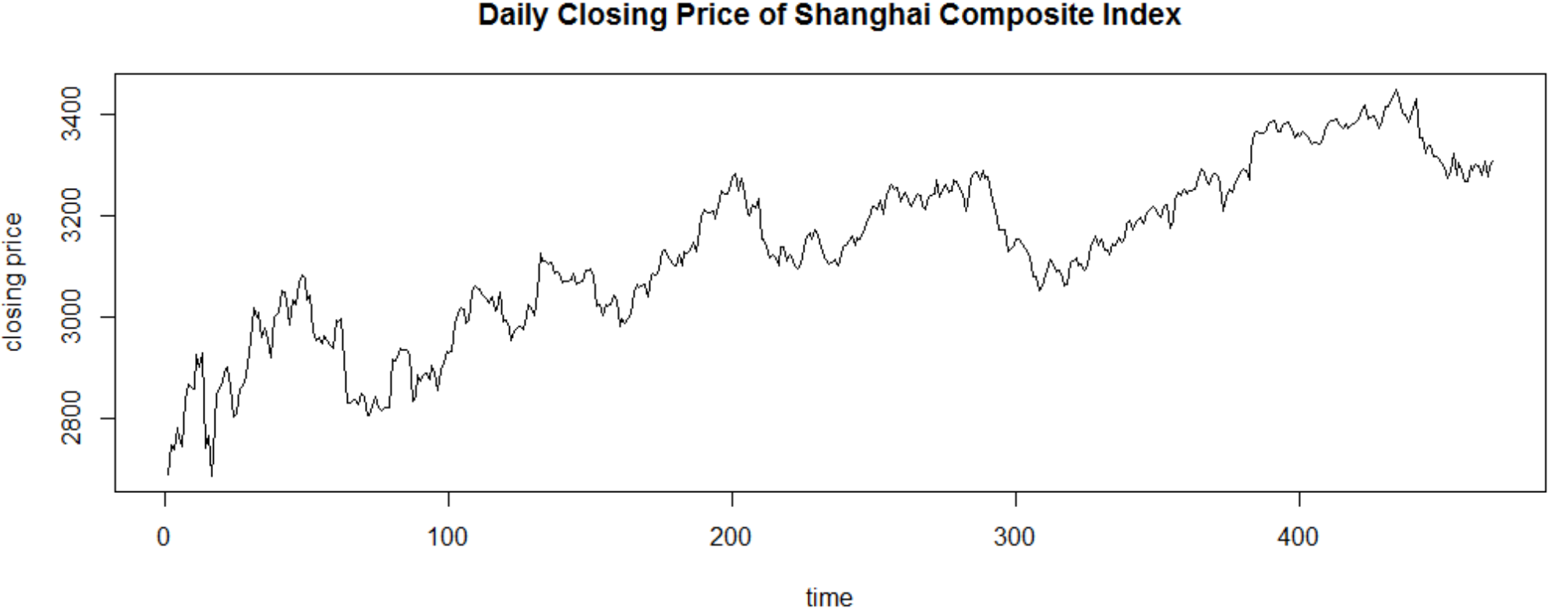
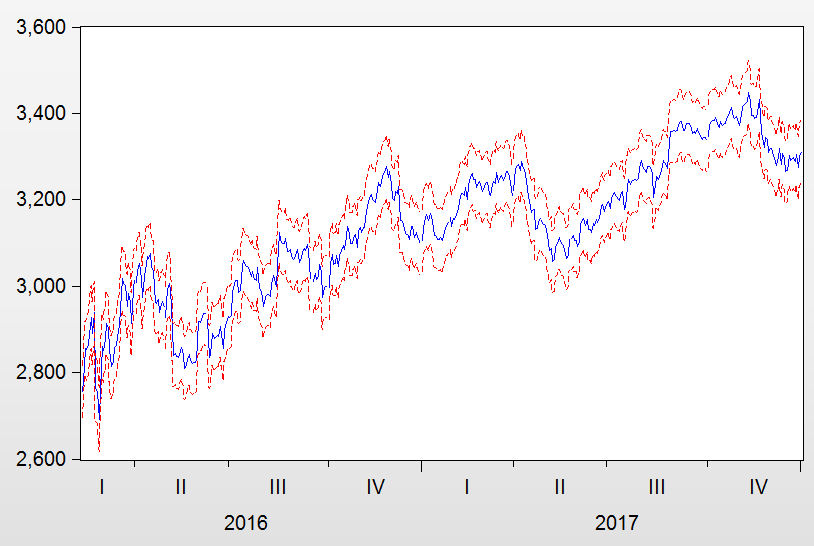
本文主要研究内容为应用时间序列模型对股票的价格趋势进行研究,研究价格序列的数据特征。通过提取序列中的有效信息来建立有效的模型,得到有效的股票价格预测结果。主要研究的基本内容分为四个方面——时间序列分析简介,主要内容为介绍时间序列的基本概念和基础模型;使用ARIMA模型对股票价格序列进行建模,以2016年至2017年两年间的上证综合指数日收盘价数据为例建立ARIMA模型,并对2018年前10个工作日的上证综合指数收盘价价格及趋势做出预测;使用ARIMA模型对股票5日移动平均序列进行建模,以2016年至2017年两年间的上证综合指数5日均线数据为例建立ARIMA模型,并对2018年前10个工作日的上证综合指数的5日移动平均值以及日收盘价的价格趋势作出预测;对上证综合指数日收盘价序列ARIMA模型的残差序列拟合GARCH模型以改进原有模型,并重新对2018年前10个工作日的上证综合指数收盘价价格及趋势做出预测。
本文主要研究思路如图:
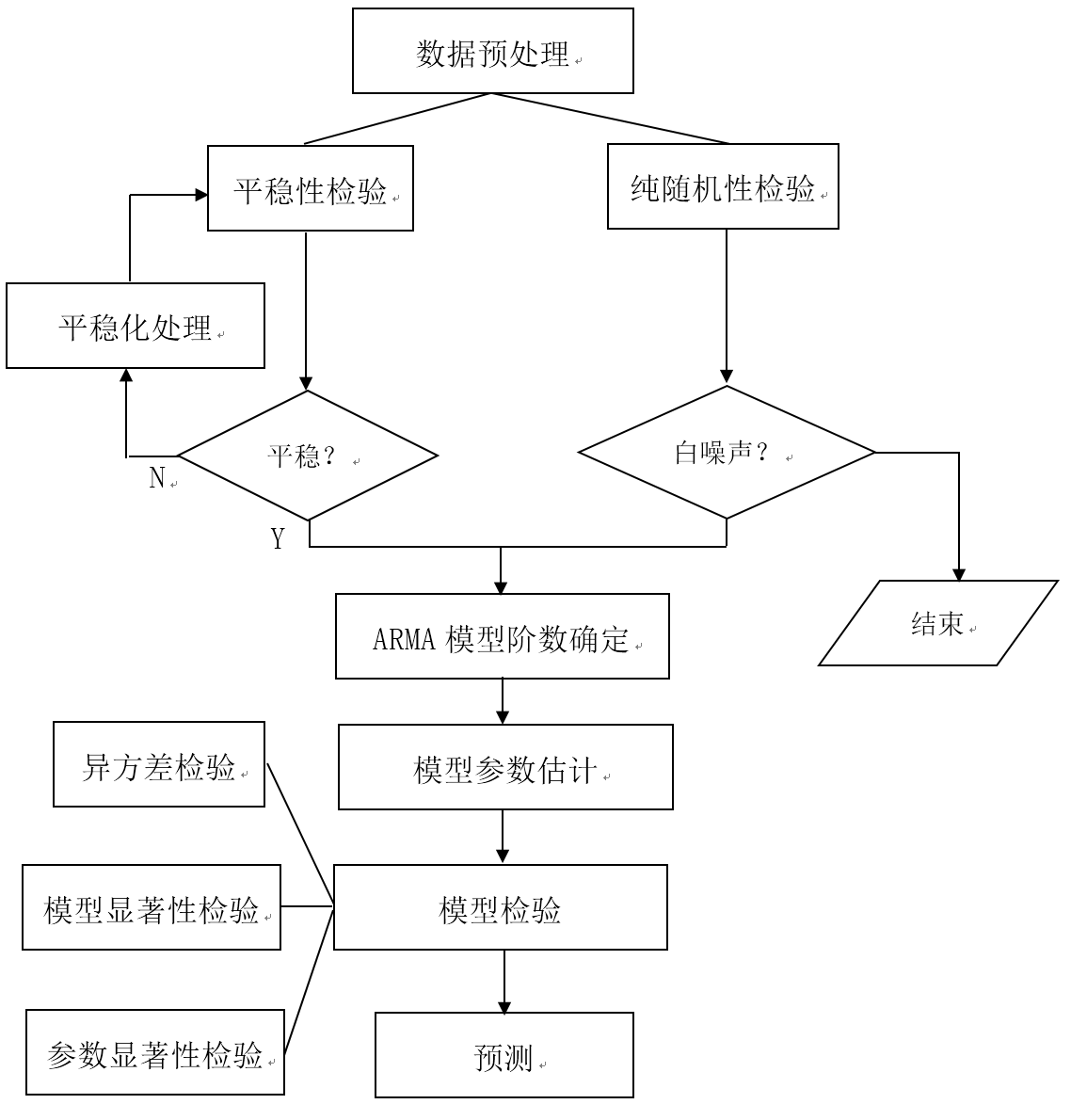
图 1.1 研究思路图
第2章 时间序列模型简介
时间序列数据即按照时间顺序排列的数据,是随着时间的推移观察到的数据。而为了得到事物的规律性探究事物与时间之间的关系,人们常常会随时间发展的先后顺序进行观测数据。这些观测到的数据有着比较独特的性质,将来的数据通常会以某种随机的方式依赖于当前得到的观测数据,这也使利用过去的数据来预测未来的特征成为可能[14]。
2.1基本概念
2.1.1 平稳性
大部分时间序列模型是建立在平稳性的假设下的。对于一个平稳的时间序列,平稳性意味着序列随时间产生特定的行为,有固定的特征,则有很高的可能性认为在未来的某一时刻数据具有同样的特征,可以产生同样的行为。故在建模前讨论序列的平稳性是极其必要的。大多数时候,在建立时间序列模型之前需要将序列平稳化处理。
时间序列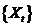 称为严平稳的,如果满足条件:对于所有
称为严平稳的,如果满足条件:对于所有 ,任意
,任意 个正整数
个正整数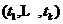 ,
,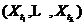 的联合分布与
的联合分布与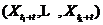 的联合分布是相同的。可以看出,严平稳要求
的联合分布是相同的。可以看出,严平稳要求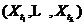 的联合分布时间平移后保持不变。
的联合分布时间平移后保持不变。
时间序列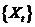 称为弱平稳的,如果满足条件:(1)
称为弱平稳的,如果满足条件:(1)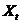 的所有二阶矩都存在;(2)
的所有二阶矩都存在;(2)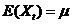 ,
,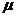 为常数;(3)
为常数;(3)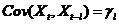 ,
, 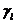 只依赖于
只依赖于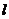 ,即协方差只与时间差有关而与时间点无关。弱平稳性意味着数据的时序图显示出数据在一个常数水平上下以相同幅度波动。实际应用中,所处理的时间序列数据达到弱平稳性即认为序列平稳。
,即协方差只与时间差有关而与时间点无关。弱平稳性意味着数据的时序图显示出数据在一个常数水平上下以相同幅度波动。实际应用中,所处理的时间序列数据达到弱平稳性即认为序列平稳。
2.1.2 纯随机性
对于给定时间序列,如果序列是纯随机的,完全没有规律可言,即序列没有可提取的可用信息,那么这个序列是无用的。研究纯随机的序列是毫无意义的。在建立时间序列模型之前讨论序列的纯随机性也是很重要的,有利于选取可用的 数据来进行进一步的研究。
具有纯随机性的序列也称白噪声序列。对于给定序列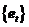 ,如果所有观测值都是独立同分布的, 称之为白噪声序列,如果满足:(1)
,如果所有观测值都是独立同分布的, 称之为白噪声序列,如果满足:(1)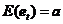 ,
,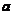 为常数;(2)
为常数;(2)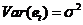 ,
,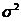 为常数;(3)
为常数;(3)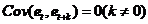 ,即不同时间点的数据不相关。
,即不同时间点的数据不相关。
- 自相关函数
首先给出自协方差函数的定义。对于平稳时间序列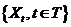 ,任取
,任取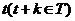 ,定义
,定义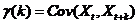 为时间序列
为时间序列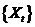 的延迟
的延迟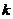 阶自协方差函数。对于平稳序列,容易得到平稳随机序列具有常数方差。由延迟
阶自协方差函数。对于平稳序列,容易得到平稳随机序列具有常数方差。由延迟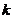 阶自协方差函数的概念可以等价得到延迟
阶自协方差函数的概念可以等价得到延迟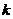 自相关系数的概念,可以看作是相关系数推广到时间序列中的概念。
自相关系数的概念,可以看作是相关系数推广到时间序列中的概念。
两个随机变量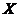 和
和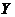 的相关系数定义为
的相关系数定义为
以上是毕业论文大纲或资料介绍,该课题完整毕业论文、开题报告、任务书、程序设计、图纸设计等资料请添加微信获取,微信号:bysjorg。
相关图片展示:
课题毕业论文、开题报告、任务书、外文翻译、程序设计、图纸设计等资料可联系客服协助查找。



