摘 要

本文借助Matlab和Midas软件，以苏岭山大桥为工程背景，进行系杆拱桥吊杆索力优化问题的研究。首先计算出苏岭山大桥索力的影响矩阵，然后将影响矩阵代入Matlab 软件中的PSO算法工具箱，进行优化处理。最后将得出的索力分配方案代入有限元模型，与优化之前索力配置下的桥梁状态进行比较。

论文主要研究了影响矩阵法和PSO算法对系杆拱桥索力优化问题的适用性。

研究结果表明：本优化方法可以快速方便地优化系杆拱桥索力配置的问题。

本文的特色：影响矩阵法的运用，使优化过程中可以考虑多个荷载状况，一步得到最优化的结果。

关键词：索力优化；影响矩阵法；粒子群算法；成桥状态

Abstract

With the help of Matlab and Midas software, this paper takes the Sulingshan bridge as the engineering background to study the optimization of the cable force of the tied arch bridge suspender. First, the influence matrix of the cable force of the SuLingshan bridge is calculated, and then the influence matrix is replaced by the PSO algorithm toolbox of Matlab software to optimize the processing. Finally, the cable tension distribution scheme is replaced by the finite element model, and compared with the bridge state before cable optimization.

This paper mainly studies the applicability of the influence matrix method and the PSO algorithm to the cable force optimization problem of tied arch bridge.

The results show that the optimization method can quickly and conveniently optimize the cable force distribution of tied arch bridges.

The characteristic of this paper is the application of the influence matrix method, so that many load conditions can be considered in the optimization process, and the optimal results can be obtained at one step.

Key Words：Influence matrix method；Cable force optimization；Particle swarm optimization；completion state

目录

1 绪论 6

1.1 系杆拱桥简介 6

1.1.1 系杆拱桥的概念 6

1.1.2 系杆拱桥受力特征 6

1.1.3 系杆拱桥发展历程 6

1.2 系杆拱桥的分类及各自特点 9

1.2.1柔性系杆刚性拱 9

1.2.2刚性系杆柔性拱 9

1.2.3刚性系杆刚性拱 10

1.3索力优化问题研究现状 10

1.3.1 索力优化问题基本概念 10

1.3.2 成桥索力优化问题研究现状 12

1.3.3存在的问题 13

1.4本文研究内容 14

2 多荷载情况下基于影响矩阵的吊杆索力优化方法 15

2.1引言 15

2.2 影响矩阵的原理 15

2.3 有限元软件计算影响矩阵 17

2.4 影响矩阵在多荷载情况下的利用 18

2.5 本章小结 18

3 利用微粒群优化算法分析吊杆索力 19

3.1 群智能算法简介 19

3.2 PSO 算法概述 20

3.2.1 原始PSO算法 20

3.2.2 具有惯性权重的标准PSO算法 21

3.2.3 具有收缩因子的PSO算法 22

3.3 Matlab 微粒群工具箱介绍 22

3.4 本章小结 24

4.算例 25

4.1工程背景 25

4.2 建立有限元模型 25

4.3 计算影响矩阵 27

4.4 影响矩阵的验证 27

4.5 利用PSO算法得到最优解 27

4.5.1 目标函数 27

4.5.2 主函数参数设定 29

4.5.3 PSO算法优化过程 29

4.6初始索力与优化索力后的梁单元应力对比 33

4.7 本章小结 34

5结论与展望 35

5.1结论 35

5.2 展望 35

致谢 36

附表1 1

附表2 1

参考文献 2

1 绪论

1.1 系杆拱桥简介

1.1.1 系杆拱桥的概念

在世界历史上，早期出现的桥梁一般是采用了梁、拱、吊这些形式简单，结构单一的桥梁，造型清晰和结构受力明确是这些结构最鲜明的特征。在人类文明规模发展扩大的过程中，人们不断地改造着自身的周围环境，工程技术也随之诞生。在现今的生活中，日新月异的科学技术的进步和知识边界的无限拓宽以及在大量工程中对各种桥梁形式的实践、优化、组合，让我们发展出更加多样、实用的桥式结构，其间的组合也更加的科学、合理。

拱桥结构在经过人们在工程实际中的探索和运用后，从远古时代单一的拱式体系，发展出了新的组合结构体系——拱梁组合、拱吊组合等等。组合结构体系是由两种或两种以上的基本结构如梁、拱、板、杆等组合而成的，相较于单一结构体系，组合结构在力学性能和材料用量上更有优势。拱梁组合体系是将拱肋和梁组合起来共同承受荷载的组合结构，拱肋承受压力，梁承受弯矩，两者组合在一起充分发挥拱、梁各自的特点和组合作用。传统意义上系杆拱桥中的系杆仅承受拱肋产生的水平力，并不承受桥面荷载。而拱梁组合体系桥梁的系杆(系梁)不仅承受水平力，而且还承受桥面荷载产生的弯矩。我国将传统意义上的系杆拱桥和拱梁组合体系桥梁统称为“系杆拱桥”。

1.1.2 系杆拱桥受力特征

系杆拱桥结构中，上部结构主要组成部分是拱圈、吊杆、系杆等构件。在拱桥结构中，拱肋作为主要承重构件，桥梁的荷载基本上都是传递给拱肋，所以拱肋会承受比较大的轴向压力和一定的弯矩。吊杆是将桥面系荷载传递至拱肋的传力构件，一般有刚性吊杆或柔性吊杆两种形式承受拉力。在布置吊杆张力的过程中，不同的布置形式会对桥梁结构的内力分布有显著的影响。在调索的过程中存在一组吊杆索力布置能使桥梁在已经确定的荷载作用下，打到受力性能最优的情况，这个吊杆索力即称为最优索力；系杆(系梁)承受拱肋产生的水平拉力，还承受桥面荷载产生的弯矩，是承受拉弯影响的梁式构件。系杆的受力情况与拱肋、吊杆的刚度有关，拱肋的刚度越大，则系杆承受的轴向拉力越大，弯矩越小。

1.1.3 系杆拱桥发展历程

系杆拱桥第一次出现在19世纪后期的欧洲。1858年刚性梁柔性拱的系杆拱桥专利由奥地利人兰格尔(Josef Langer)申报，在这项专利中提出拱肋和吊杆的连接采用铰接形式，拱肋上只有轴力，没有弯矩。现代系杆拱桥的雏形出现，称为 Tied Arch(系杆拱)。在1881年Langer设计了第一座刚性梁柔性拱系杆拱桥，此后刚性拱刚性梁、刚性拱柔性梁两种概念也被提出并运用于实际工程中。

随着对系杆拱桥在实际中的运用和研究的深入，尼尔森体系被提出。在该体系中利用斜吊杆取代之前Langer桥中的竖吊杆，大幅度提高了桥梁结构刚度，最早由尼尔森(Q.F.Nielsen)提出，所以被称为尼尔森体系，并在1929年获得专利权。1929年第一座尼尔森体系桥梁——费马恩松德桥(Fehrnamsund)在德国建成，桥梁主跨长248.4m，矢高43m，桥面宽度21m，桥面由单线铁路与三车道公路组成。于1992年建成的日本新滨寺桥，创造了尼尔森体系钢桥跨度的新记录，跨度254m。

在兰格尔、尼尔森体系的提出之后，新的系杆拱桥形式——网络拱桥出现了。网络拱桥(NetworkArch)的专利由挪威爱吉尔学院Per Tveit教授于1955年申请。网络拱桥中，吊杆的布置形式采用网络状形式，其中的部分斜吊杆会与其他吊杆相交至少两次。1963年斯泰恩谢尔桥--第一座网络状吊杆结构的系杆拱桥在挪威建成，主梁长度80m。

1987年，斜靠式系杆拱桥的理念出现。在斜靠式拱桥的设计中，两片竖直主拱与两片斜靠拱组，构成空间整体受力体系，两片竖直拱肋承受主要荷载，斜拱则增强了桥梁整体抗扭和抗倾覆的能力，承受部分荷载。西班牙著名建筑师圣地亚哥·卡拉特拉瓦设计了第一座斜靠式拱桥Bacde Roda桥，该桥种外观新颖，曲线优美富有张力，成为所在城市著名的地标建筑，吸引了无数的游人参观。

目前系杆拱桥正在我国兴起。2003年建成的卢浦大桥，横跨黄浦江，结构形式是中承式变高钢箱拱桥，跨径组合为 100m 550m 100m。体系为三跨中承式，拱肋会产生一定的水平推力。中跨主梁以简支结构的形式布置在梁拱交合的横梁之上，边跨主梁采用与拱肋固结的形式，使结构更适合以软土地基为主的上海等周边地区。（图1-1）

图1-1 上海卢浦大桥

2007年建成的重庆菜园坝长江大桥，采用钢混组合刚构体系，中跨长度420m，边跨长度102m。该桥拱肋为高 4m 、宽 2m 的提篮形钢箱拱，主梁为 11m 高钢桁梁。由于主梁刚度较大，边跨采用预应力混凝土 Y 形刚构。该桥中跨系杆与边跨系杆分开设置，独立锚固，并在边墩增设竖向系杆索。多套相对独立的拉索体系可分别张拉和调节，方便对大桥主体结构进行内力与线型的调整、控制。（图1-2）

图1-2 重庆菜园坝长江大桥

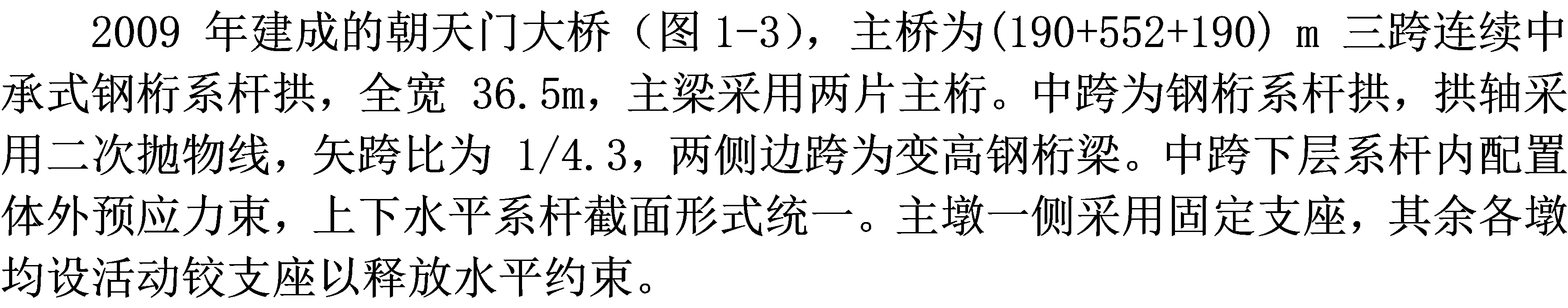
图1-3 重庆朝天门大桥

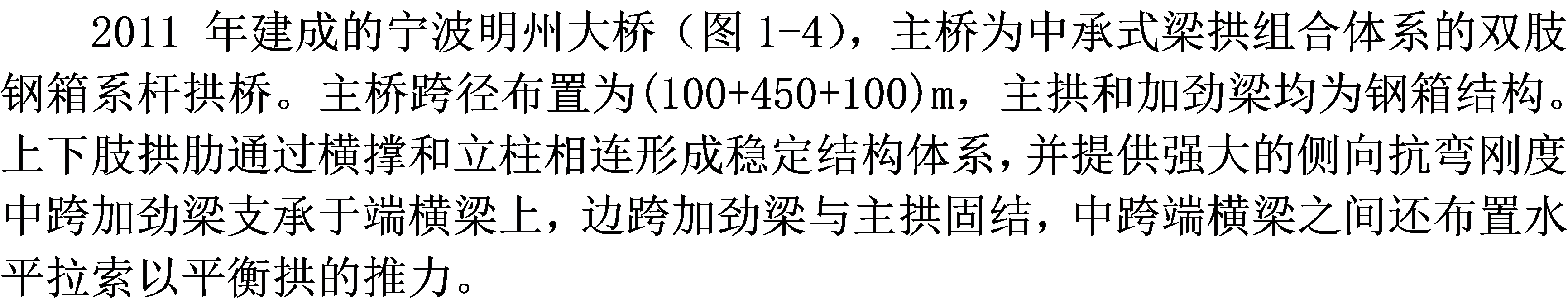
图1-4 宁波明州大桥

1.2 系杆拱桥的分类及各自特点

1.2.1柔性系杆刚性拱

假设系杆和吊杆为柔性杆件，即系杆和吊杆无法承受弯矩、压力，只能承受拉力在这种体系中。按照力学原理，只有当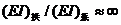，即拱圈的惯性矩比系杆大无数倍时，上述假设才能合理。但是在现实情况中，系杆构件是拥有一定刚度的，并不是完全柔性，所以在结构受力的分析中会分配到一定的弯矩。考虑到系杆的刚度远远小于拱肋的刚度时，系杆上承受的弯矩值很小，所以当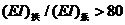时，我们认为所有弯矩由拱圈承受，系杆部分仅仅承受轴向拉力。这样的假定可以充分发挥材料的性能，减少了建设过程中钢材的使用量，降低了墩台的负重，因而软土地基上十分适用。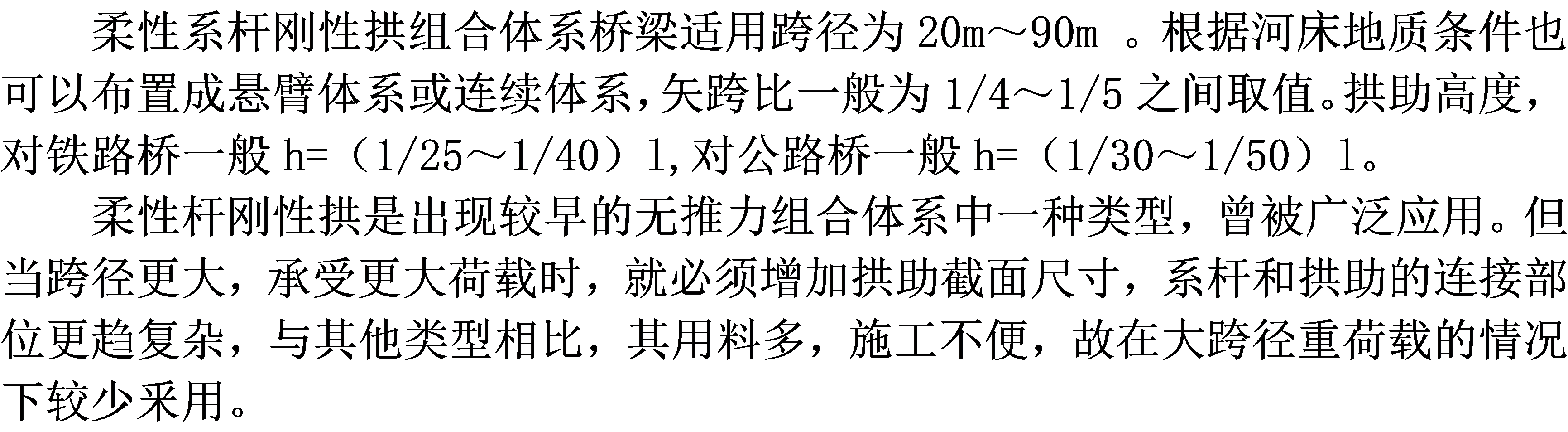

1.2.2刚性系杆柔性拱

刚性系杆不仅能承受拱的推力，还要承受弯矩，拱助只承受轴向力称为柔性拱。这种体系是以梁为主要承重结构的体系，故又被称为朗格尔拱。但是柔性拱不承受弯矩在实际上是不可能的，当拱助承受的弯矩远比系杆小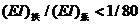，时即可以忽略拱肋中的弯矩，此时可以认为拱助只承受轴向压力，故称为柔性洪。这种体系相当于把桁架弦杆与梁结合起来，以梁为受力主体，组成具有刚性梁的曲线桁架。它的特点是内力分布均匀，刚度大，不会发生拱的S形变形。其次是刚性系杆便于岸上拼装拖拉就位，适合于河中不便架设脚手架进行就地安装的河段上建桥。刚性系杆柔性拱也往往由于美观而被采用。

系杆柔性拱的适用跨径可达100m，矢跨比一般为1/5～1/7，拱助高度通常取（1/100～1/120）l，刚性系杆高度对公路桥h= （1/25～1/35）l，对铁路桥h= （1/22～1/30）l。

1.2.3刚性系杆刚性拱

1.3索力优化问题研究现状

1.3.1 索力优化问题基本概念

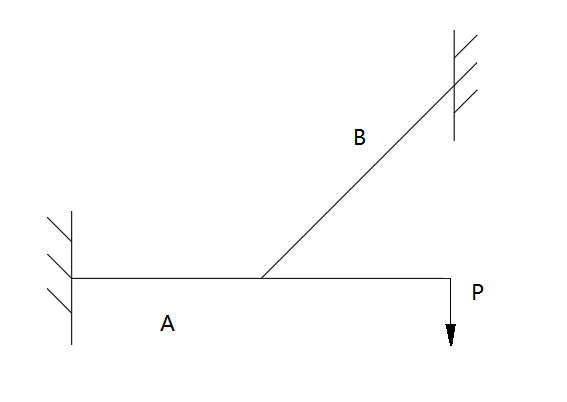
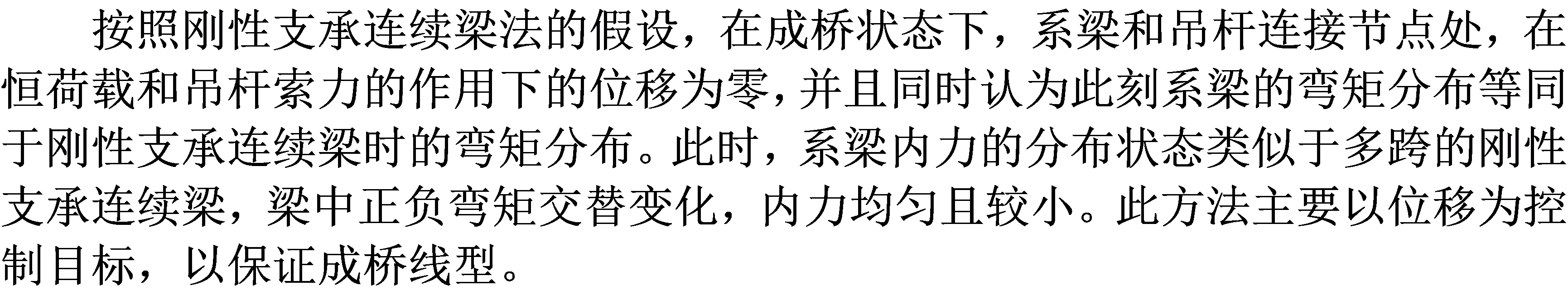如下图所示由索和梁组成的一个一次超静定结构，索的索力可以通过张拉索来调整其大小。

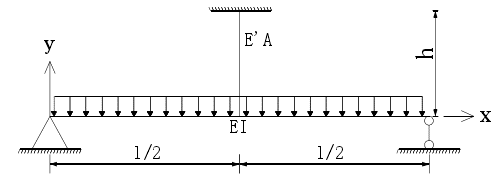
以拉索索力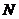为超静定力，其受力状态可以通过静力平衡条件算得，支点反力 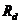和梁的弯矩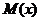分别为：

（1-1）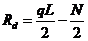

（1-2）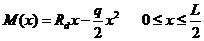

在不主动张拉拉索的情况下，由变形协调条件计算可得拉索索力为：

（1-3）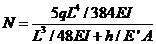

为了简化讨论，令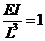 , 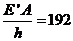，则（1-3）变为

（1-4）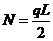

此时梁的弯矩图如下图所示，这一状态对应于系杆拱桥一次落架时的恒载内力状态。

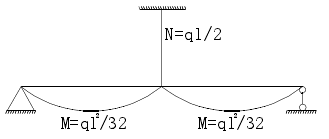
为了优化梁的受力，现在对拉索的索力进行调整，现选取以主梁的弯矩平方和最小为目标，则目标函数为:

（1-5）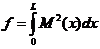

将式(l-2)、式(l-4)代入式(l-5)中，得到使该目标函数值最小的驻值为：

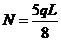
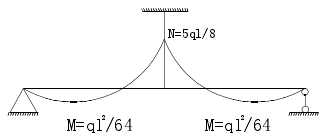
此时梁的弯矩图如上图所示，这一状态对应于吊杆索力优化后系杆拱桥的恒载内力状态。这时的内力状态是通过索的张拉来实现的，正是这一张拉力改善了梁的受力状态。

1.3.2 成桥索力优化问题研究现状

在确定索结构桥（斜拉桥、系杆拱桥等）内力方面，有许多方法。按文献介绍，根据其成桥目标的不同和实现成桥所用方法不同，可分为以下几种：

（1）按成桥目标分类

1） 刚性支撑连续梁法

在系杆拱桥结构中，吊杆是符合胡可定律的弹性体，假定吊杆是弹性支承，会在影响力的作用下发生弹变化，从而使系杆出现标高变化，产生弯曲变形，进而在系杆体内产生次内力。

2） 力的平衡法

在此方法下，结构的最佳受力状态的目标是使结构关键截面的内力(一般是应力、位移、轴力等)达到最佳状态。主梁上各点的标高可以通过设计预拱度来调整。刚性支承连续梁法以位移作为控制目标，另外一种确定成桥时吊杆张拉力的方法就是直接以截面内力为控制目标。

系杆结构的拱桥中，我们把直接承受活荷载的系杆（系梁）当作我们的主要的研究对象，控制吊杆与系杆连接处的关键截面应力值（一般是弯矩）变化，再将预应力钢筋和混凝土收缩、徐变对关键截面的弯矩的影响综合考虑，形成控制变量。则当成桥时，吊杆张拉力应能使系梁内控制截面的弯矩在恒载和吊杆拉力的作用下，达到设计者所指定的弯矩状态。以此为指导思想，力的平衡法以截面弯矩为主要控制目标来确定恒载作用下合理成桥状态时吊杆张拉力的大小。

3） 刚性吊杆法

4） 最小能量法

对于之前所叙述的几种方法，将位移或者内力作为确定成桥状态的主要手段。但是建成一座预应力混凝土系杆拱桥，需要经历复杂的施工过程，如果此时采用单一的目标来控制，往往是不合适的。所以我们需要另一种综合性更强的方法来完成这项工作。如果需要考虑多种因素比如内力状态及成型的线型状态等，这个问题就可以转化为一个多个约束条件下的函数最优解的问题。所以首先，我们要确定一个目标函数，也就是通常所说的评判指标；然后，在设定的约束范围内，寻找我们所需要的最优解。这种方法在优化原理中称为二次规划法。

如果以系梁的弯曲能量为目标函数，求出能同时满足内力和线型两种成型状态条件下，目标函数值最小时的解。将这组解作用在桥梁模型里，便能得到一种较为合理的成桥状态。这种以能量作为目标函数的方法，就是我们通常所说的能量法。

以上是毕业论文大纲或资料介绍，该课题完整毕业论文、开题报告、任务书、程序设计、图纸设计等资料请添加微信获取，微信号：bysjorg。

相关图片展示：