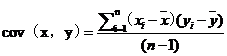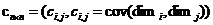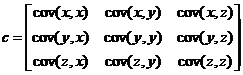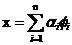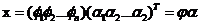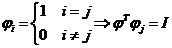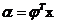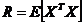基于PCA算法的人脸识别技术分析毕业论文
2020-04-09 15:21:34
摘 要
随着社会的稳步发展,社会各方面的矛盾也慢慢暴露了出来,人们的安全意识也越来越完备。在这种时代大前提下,一种准确的,方便的,身份识别方式被大众所需要。于是人脸识别就成为了当前社会在身份识别方面研究的热潮。
本篇文章,运用MATLAB软件来进行实验仿真,实现了基于PCA算法的人脸识别系统,了解和掌握了主成分分析算法的主要思想和它的数学理论支持,以及PCA算法在人脸识别中的具体应用和具体的实现步骤。主要通过PCA算法对人脸库中的人脸图像进行
特征提取和分析,并实现降维,可以直观的看到降维后的人脸图像,再通过源自机器学习中的SVM(支持向量机)来构建分类函数,对目标进行分类,且详细说明了PCA的基本原理和数学推导,以及其在MATLAB环境中对人脸图像进行分类的具体方法等,最终本次仿真较好的到了预期目标,对ORL人脸库中的图像基本实现无差错识别。
关键词:SVM支持向量机;主成分分析;MATLAB;
ABSTRACT
With the steady development of society, contradictions in all aspects of society are gradually exposed, and people's safety awareness is becoming more and more complete. Under the premise of this era, an accurate and convenient way of identification is needed by the public. So face recognition has become the upsurge of research on identity recognition in the current society.
In this article, MATLAB software is used to carry out experimental simulation, and the face recognition system based on PCA algorithm is realized. The main ideas of the principal component analysis algorithm and its mathematical theory support are understood and mastered, and the specific application and concrete implementation steps of the PCA algorithm in face recognition are carried out. The face image in face database is mainly implemented by PCA algorithm.
Feature extraction and analysis, and the realization of dimensionality reduction, can see the face image after dimensionality reduction intuitively, and then construct classification function by SVM (support vector machine) derived from machine learning, classify the target, and elaborate the basic principle and mathematical deduction of PCA, as well as the face image in the MATLAB environment. Finally, this simulation achieves the desired goal, and basically realizes the error free recognition of the images in the ORL face database.
Keywords: SVM support vector machine; principal component analysis; MATLAB;
目录
摘要 I
ABSTRACT II
第1章 绪论 1
1.1人脸识别的背景和发展现状 1
1.2 人脸识别的目的与意义 1
1.3 课题研究内容 2
第2章 设计方案提出与选择 3
2.1 开发环境(MATLAB)简介 3
2.2 方案设计 4
第3章 PCA算法及SVM的实现 6
3.1 PCA的基本思想 6
3.2 PCA算法的理论基础 7
3.2.1预备知识 7
3.2.2 k-l变换原理 8
3.2.3 PCA算法 9
3.3 PCA算法实现 10
3.3.1 PCA实现步骤 10
3.3.2 SVD奇异值分解 12
3.4 SVM(支持向量机)原理 13
3.4.1 SVM方法的特点 13
3.4.2 SVM的数学理论 14
3.4.3 SVM实现步骤 18
第4章 系统仿真与结果分析 20
第五章 总结和展望 28
参考文献 29
致谢 30
第1章 绪论
1.1人脸识别的背景和发展现状
人脸识别的概念于上世纪60年代提出,在发展了近20年后,由于计算机的飞速发展,以及光学成像技术取得了长足进步,迎来了其发展的黄金时期。而到了九十年代,在美德日等发达国家的带领下,人脸识别技术趋于应用。应用人脸识别技术的系统是需要应用多种专业技术的综合性系统。
而我国的人脸识别技术,在进入新世纪后的第二个十年中取的了飞速的发展,由我国科技团队自主研发的人脸识别系统,首次实现了识别准确率超过人眼的壮举,同时也标志着我国在这一领域已经跻身世界领先水平。而为了能够保持在这一领域取得长久的兴盛,人脸识别也作为一门课程渐渐进入了各大高校,为有所兴趣的大学生打开了大门。并且,该项技术在“2025中国制造”中也占有一席之地,足以见得,我国在这一领域展现的雄心。
主分量分析的本质是一种用于将高维度计算以降维的方式简化计算。此方法的主要思想,就是将分量相关的向量转换为不相关的新的向量,以此来降低数据的读取难度。而关键的问题便是,能不能在降维的同时保持较高的精度。查阅文献,现在的人类识别技术,多采用欧式距离分类。这种分类方法在构建图像骨架时,能够发挥较好的效果,但这种方法使得软件的空间感较差,同时当图像形状产生变化时有很大反应,就使得在人脸识别中,只要人稍有改变(诸如变胖了),这种分类方法下的代码就会揪住不放。因此,本文的设计便采用了了一种新的方法,应用SVM分类器来实现分类,以图解决这种问题。
1.2 人脸识别的目的与意义
人类社会发展至今天,科技越来越发达,人们变得越来越自由。以下安全问题已成为公众生活中最重要的问题之一。社会的发展促进了人们的流动,但也增加了社会的不稳定性,无论是工作还是,出入,学习等都涉及到安全问题,以往的符号密码的保护方式已经不能适应要求更高的安全保障了,在现代社会,不管去哪,身份已经成为了一个人最大的标签,甚至可以在一定程度上代表着个人身份识别已经成为人们常日生活中的一个基本问题。然而,随着互联网的遍及和交通技术的发展,人们的现实生活活动空间和虚拟空间不断扩张。在各种情况下都需要基本认证。携带越来越多的识别物品,识别过程和检测方法的需要也变得越来越繁琐。传统的身份识别方式正在慢慢显露他的弊端,例如容易被遗忘或者窃取,甚至破解等。每年,身份问题给整个社会带来的损失是巨大的,面对这种情况,我们必须找到一种更现实可靠的新型识别方式。
近年来,生物特征识别技术被广泛的应用于身份识别方面,而面部识别技术由于方便,稳定和无创性而成为了身份识别技术的主流。人脸识别信息录入方便,信息丰富。已经愈来愈多的应用于除安全问题之外的身份识别领域。
1.3 课题研究内容
从人脸识别技术兴起至今的五十多年的时间里,人脸识别技术取得了长足的进步。随着社会安全意识的提高,人脸识别技术也受到了相当的关注。近年来,大量有关身份识别的理论和算法纷纷涌现。人脸识别方法很多,每种方法各有优缺点,目前还没有一种更通用的方法适合于所有的识别场合,所以现在人脸识别更多的是综合各种方法。或者同时使用不同类型的功能。本文主要运用PCA 算
法对人脸图像进行处理,并在MATLAB上完成整个仿真系统。
本文主要的研究内容如下:
1.对此次仿真的开发环境,研究的现状背景和意义等做了大概的介绍,详细阐述了了传统的PCA算法的人脸识别流程和基本步骤,PCA算法的基本思想和数学理论,以及PCA算法是如何具体运用到人脸识别中的。为了提高分类的识别精度,同时为了输出准确率,将人脸识本的检测阶段和SVM分类器结合起来,研究了支持向量机的基本思想数学推导和面对多类分类情况下的是SVM分类器的构造方法和实现。
2.基于本文提出的核心技术来进行试验仿真,给出了基于PCA和SVM算法的人脸识别的系统的设计和实现方案,设计了简洁的人机交互界面,实时显示算法执行程度和流程进行,并对系统仿真结果进行分析,提出改进方向。
第2章 设计方案提出与选择
2.1 开发环境(MATLAB)简介
MATLAB软件系列产品可以将其通俗的理解为一个具有超强计算能力和绝佳的图像处理能力的计算器,借助MATLAB能够迅速地测试设计构想。
用于MATLAB编程的语言是一种功能强大的语言,使用者几乎不用接触太多语法,就可以轻松用它,编程效率极高。这个针对性很强的新型语言,自从推出初期就收到了受到了广大科技工作者的广泛好评。如今还在不停地更新优化。它在1984年的时候被推向市场,从那时候起,MATLAB的内核采用c语言编写。在原有的数据计算功能上又添加了图视功能。
MATLAB的特点有如下几点:
1.数值计算和符号计算功能
MATLAB机会涵盖了大部分的计算功能,且数值计算速度快,精度高。库函数功能强大。
2.强大的MATLAB编程语言
由于MATLAB语言是以c语言作为内核的。所以不管是c还是其他语言的大部分功能她几乎都可以实现。包括图形用户界面的设计。
3.具有很好的图形功能
用户可以利用图形用户界面gui制作工具,可以根据自己的需求来编写出满意的图形界面。
4.可以直接处理声音和图像文件
MATLAB支持的声音和图像文件格式很多,在MATLAB中只需要很简单的命令,就可以将声音文件或图像文件读入系统,并对它们做出相应的处理。
5.具有功能强大的工具箱
MATLAB除了基本的各种计算功能外还有各种可供选择的工具箱。基本部分中有数百个内部函数,可以满足大部分的需求,还有一大部分的具有各种功能的工具箱可以使用,包括我而本次用到的SVM工具箱。
6.使用方便,强大的扩展功能
使用MATLAB言编写的程序可以不用编译直接运行。还可以在C语言中作为数据计算引擎使用。
2.2 方案设计
经过查阅资料和老师咨询以及了解人脸识别技术的发展进程后,了解到人脸识别并不仅仅是一个传统的模式识别问题,而是一系列的工作流程进行整合的结果,并且面对不同的方面的应用,对人脸识别提出的要求也不同,人脸识别的侧重点也不同,所以说人脸识别的过程并不统一,但还是存在一个相对而来说较为一致的人脸识别过程,如下图所示:

图 2-2-1 人脸识别流程
但是这只是一个初步的流程,具体的识别步骤因算法和要求不同也不尽相同。
输入部分首先要进行人脸图像的定位和预处理,预处理也就是对现有图像进行灰度化和平维,确保在执行PCA算法时维度一致,因为我本次测试输入部分由ORL人脸数据库提供。它由40个不同性别和不同种族的人组成,确切地说,是1992年4月至1994年4月,两年期间由美国一个实验室拍摄的一系列面部图像。不同种族的人脸图像由400幅灰度图像组成,每幅图像10幅,大小为112×92。这10幅图片中的每一幅都显示了面部表情和面部细节的细微变化,这些变化可以通过肉眼来区分,比如睁开眼睛或闭上眼睛。张开嘴或者闭嘴。脸部姿势也会改变。平面旋转和深度旋转可以达到20度,并且脸部尺寸也可以改变达10%。它是人脸识别的理想数据库。也是当前应用最为宽泛的人脸数据库。因此本次仿真就决定将orl人脸库作为本次实验的人脸数据库,将每个人的十张人脸图中的前五张作为训练数据集录入,后五张图像作为测试数据集录入。由于本次仿真使用现成的数据库。所以可以省略预处理这一步骤,但这一步骤在人脸识别中大多时候是不可或缺的。
而在特征提取和降维这部分,就采用最为方便和广泛的PCA算法,也即是主成分分析法。主要原理和实现方法后续章节详述。
最后的匹配识别部分通过PCA算法提取的训练样本投影集和测试样本投影集计算欧氏距离来实现匹配识别,
后来在实验过程中查阅资料了解到,SVM分类器可以用于此类分类情况,还可以输出识别率和提高识别率,所以最终采用SVM分类器来实现匹配识别。主要原理和实现方法后续章节详述。
综上所述,本次人脸识别系统总体流程如下:
1.读取训练数据
2.主成分分析降维
3.数据规格化(去除数据单位因素对分类造成的不良影响)
4.SVM训练
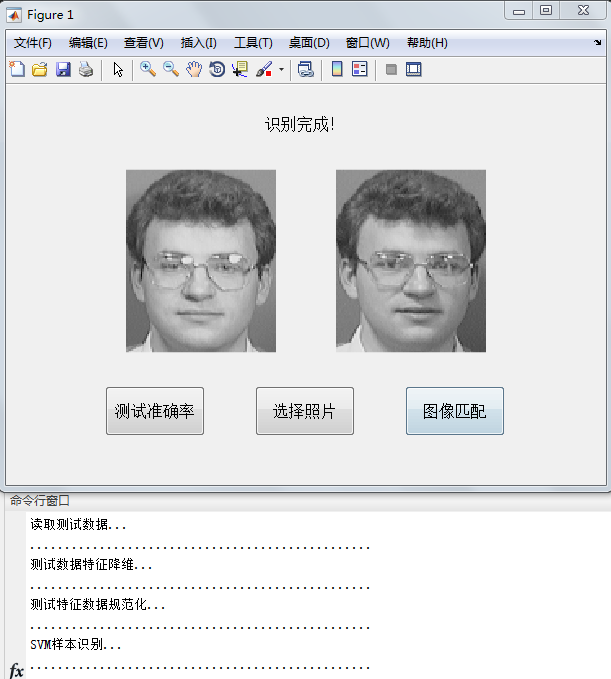
5.读取测试数据,降维,规格化。
6.利用SVM训练产生的分类函数对其进行分类
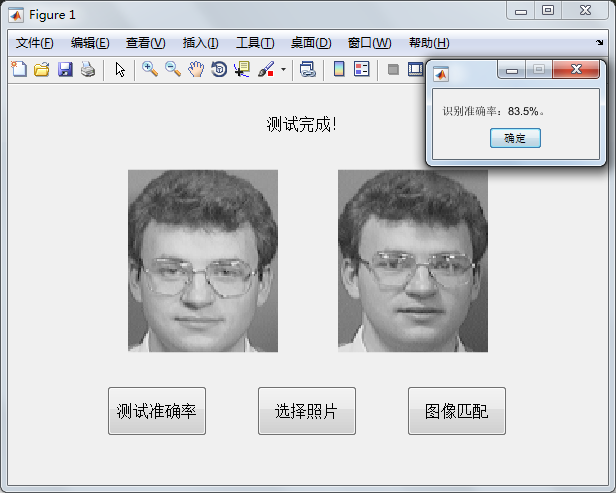
7.计算正确率
第3章 PCA算法及SVM的实现
3.1 PCA的基本思想
PCA(principal components analysis)即主成分分析,顾名思义,它可以把表征一个事物最为重要的特点提取出来,丢弃掉一部分不重要或者相对来说不重要的特征,提取事物的本质因素,从而使复杂的问题简化,而PCA算法也是图像处理方面常用的降维方法,他的基本思路就是把一个高维的图像降低成一个低维的图像,多矩阵降维为一列矩阵,使得运算更加简单,通俗来讲就是如果想要认出一个人的身份,可以通过他的面部器官来辨认,如果我们可以通过某个两个或几个器官就可以达到识别身份的目的的话,就可以大大减少工作量,这就是PCA的核心思想。
PCA方法的根本原理是通过kl变换将表述这个图像的主要特征提取出来,产生一个特征人脸空间。当需要进行识别时,将测试图像投影到获得的特征空间中,获得一组投影系数,然后和测试图像进行比对,完成目标识别任务。
PCA也是图像处理中常用的降维方法。众所周知,在处理数字图像问题时,例如经常使用的图像查询问题,在数以万计甚至数百万甚至更多的数据库中进行类似的查询。在图片中,通常是一些更复杂的特征被提取。图像中有许多这样的特征点,并且每个特征点可能需要多维矢量来表示,而数据库中也有数量庞大的图片,这样的检索难度是很大的,如果我们在检索之前就对数据库中的矢量进行PCA降维,就可以大大减少工作量。
3.2 PCA算法的理论基础
一个矩阵的维数,如何选择一个标准的正交基,使得投影矩阵的正交基可以代表矩阵的最大程度。这就是PCA想要解决的问题。当然,这只是一个普遍的说法。
3.2.1预备知识
样本x和样本y的协方差
| (3.1) |
正协方差表示x和y是正相关的。当协方差为负时,x和y是负相关的。当协方差为0时,x和y是独立的。如果说明的是x和x之间的协方差的话,代表的就是x的方差。
如果需要计算多维数问题时,那么我们就会想到应用矩阵来处理这些数据,在此给出协方差矩阵的定义:
| (3.2) |
这个定义从公式上来看就很好理解,举一个简单的三维数组的协方差计算的例子,假设有一个三维的数据集(x,y,z)。那么它的协方差矩阵为:
| (3.3) |
由公式3.3可得,协方差矩阵是一个对称的矩阵,而且对角线上的元素由每个维度的方差来组成。从协方差矩阵的定义来看,只要稍加推导,就可以得出一本关于协方差矩阵的重要性质。
而对角线上的元素大小也能够显示部分特征。元素越大说明它的相关性就越高。
对于维度稍高的目标来说,协方差矩阵的计算数据量是十分庞大的。PCA算法的目标就是通过基变换对协方差矩阵进行最佳变换,选取贡献率高的主成分,实现降维目的。
3.2.2 k-l变换原理
K-l变换,也可以称为最优正交变换,这一变换是PCA算法的理论基础,是一种常用的正交变换,下面对k-l变换做一个基本介绍:
假设x为n维的随机变量,x可以用n个向量的加权和来表示:
| (3.4) |
在式子中,α是加权系数,φ是基向量,如果将此公式用矩阵表示的话,如下所示:
| (3.5) |
取基向量为正交向量,即为
| (3.6) |
则系数向量为
| (3.7) |
综合上述公式以及理论,通过以下步骤可以求出K-L的展开式系数:
1.求随机向量x的自相关矩阵
| (3.8) |
2.求出自相关矩阵或协方差矩阵R 的本征值和本征向量
以上是毕业论文大纲或资料介绍,该课题完整毕业论文、开题报告、任务书、程序设计、图纸设计等资料请添加微信获取,微信号:bysjorg。
相关图片展示:
课题毕业论文、开题报告、任务书、外文翻译、程序设计、图纸设计等资料可联系客服协助查找。