摘 要

随着无线通信技术的高速发展，人们对于天线的小型化与宽带化的要求越来越高。但是，传统的天线基本上都是基于欧式几何的形状设计的，这些天线的尺寸大多为半波长大小，而且最大的缺点就是带宽很窄。因此，需要探索一种新理论和方法来解决天线的宽带化以及小型化问题。而经过研究发现，将分形理论应用到天线技术中，可以有效的拓展天线的带宽。

本文首先介绍了宽带天线的研究背景以及国内外发展状况，并详细说明了几种天线宽带化技术，并在其中介绍了分形技术的一些特点以及近些年国内外所研究出的分形天线，接着又详细介绍了分形理论以及实现分形的数学方法。这些理论都为实现设计基于分形结构的宽带天线提供了理论支持。

其次，本文将分形理论与天线技术相结合，设计出了两款基于Koch分形结构的宽带天线。第一款天线将Koch分形结构与八边形辐射贴片相结合，其相对带宽达到97%。第二款天线是将Koch分形结构与单极子天线相结合，设计了一款谐振频率为2.45GHZ的宽带天线，其相对带宽达到32.7%。这两款天线都满足宽带天线的带宽要求。

最后，将设计出的天线进行加工，并测量其特性参数，其测量结果与天线的仿真结果基本相似，从而可以验证将分形结构与天线技术相结合确实可以有效拓宽天线的带宽。

关键词：分形结构；宽带天线；分形天线

Abstract

With the rapid development of the wireless communication technology, people are increasingly demanding the miniaturization and broadband of antennas. However, the conventional antennas designed are basically based on the shape of the European geometry. The size of these antennas is mostly half the wavelength, and the biggest drawback is that the bandwidth is very narrow. Therefore, it is necessary to explore a new theory and method to solve the problem of broadband and miniaturization of antennas. After research, we found that applying the fractal theory to antenna technology can effectively expand the bandwidth of the antenna.

Firstly，This article introduce the research background and development status of broadband antennas, and explained several antenna broadband technologies in detail, and introduced some characteristics of fractal technology and fractal antennas researched at home and abroad in recent years. It also introduces the fractal theory and the mathematical method of fractals in detail. These theories provide theoretical support for the design of broadband antennas based on fractal structures.

Secondly, this paper combines fractal theory with antenna technology and designs two broadband antennas based on Koch fractal structure. The first antenna combines a Koch fractal structure with an octagonal radiating patch, with a relative bandwidth of 82.7%. The second antenna is a combination of a Koch fractal structure and a monopole antenna. A broadband antenna with a resonant frequency of 2.45 GHz is designed, and its relative bandwidth is 22.7%. Both antennas meet the bandwidth requirements of broadband antennas.

Finally, the designed antenna is processed and its characteristic parameters are measured. The measurement results are basically similar to the simulation results of the antenna, so that it can be verified that combining the fractal structure with the antenna technology can effectively widen the bandwidth of the antenna.

Key Words：Fractal structure; wideband antenna; fractal antenna

目 录

第1章 绪论 1

1.1 研究目的及意义 1

1.2 国内外天线宽带化的研究现状及发展历程 1

1.2.1 降低等效谐振电路Q值 1

1.2.2 表面刻槽技术 2

1.2.3 电磁耦合馈电 2

1.2.4 分形技术 2

1.3 本论文的结构安排 3

第2章 相关理论概述 5

2.1 分形基本理论 5

2.2 分形的维数 5

2.3 常应用到天线中的分型结构 6

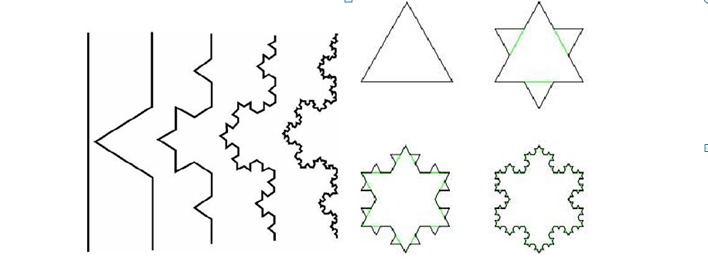
2.3.1 Cantor集合 6

2.3.2 Koch曲线 7

2.3.3 Siperpinski集 8

2.3.4 Peano曲线 8

2.4 天线的性能参数 9

2.4.1 输入阻抗 9

2.4.2 反射系数与驻波比 9

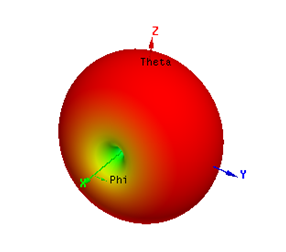
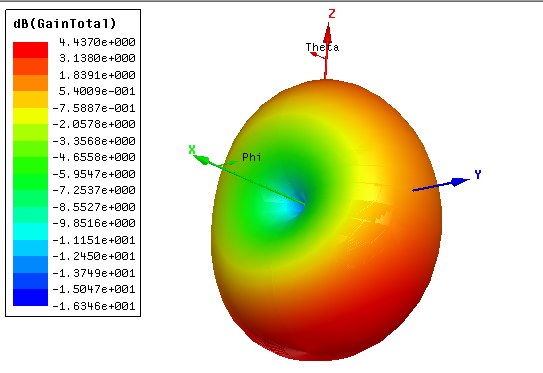
2.4.3 方向图 10

2.4.4 天线的方向性系数 11

2.4.5 天线的效率 12

2.4.6 天线的增益系数 12

2.4.7 天线的带宽 13

2.5 HFSS天线仿真软件简介 13

2.6 本章小结 14

第3章 分形天线的设计 15

3.1 引言 15

3.2 天线一的设计与分析 15

3.2.1 介质基板材料的选择 15

3.2.2 天线一结构的设计 15

3.2.3 结果分析 20

3.2.4 天线一的制作与测量 21

3.3 天线二的设计与分析 22

3.4 小结 25

第4章 总结与展望 26

参考文献 27

致 谢 28

第1章 绪论

1.1 研究目的及意义

自从德国科学家赫兹在1887年证实了电磁波存在之后，天线技术的发展有着大约一百三十多年的历史，随着无线通信技术的发展，天线技术也得到了快速的发展。尤其是近些年新型智能无线通信系统的产生对天线提出了越来越多的要求，包括智能化特性，多频段宽带特性等。目前，宽带技术是无线通信中的一个重点研究技术，宽带技术具有多个优点，例如；

1）具有高的传输速度。宽带天线的脉冲宽度一般能够达到亚纳秒量级，带宽很宽，宽带信号在相应的频谱上拥有很宽的能量谱，带宽能够达到GHZ，能给系统提供很大的能量，这可以使宽带天线系统适合高速率无线传输应用。

2）处理增益高。宽带可以使系统拥有大的增益，使抗窄带干扰的能力变强。

3）可以提高现有的频谱利用率^[1]。宽带信号因为发射功率很低，对其他窄带信号的干扰较小，所以能够与现有的窄带并存，拥有较好的共存性，同时它也可以与其他的频率系统共享资源，因此可以提高频谱的利用率。

正是因为宽带技术拥有以上的特点，业内人士对宽带技术的研究十分重视，研究出宽带化天线具有很大的现实意义。

1.2 国内外天线宽带化的研究现状及发展历程

宽带天线在历史上的发展大致上可以分为3个阶段：宽带天线在20世纪50年代处于发展阶段，其主要应用于广播电视等一些通信；20世纪50年代至90年代初，是宽带天线的的发展高峰期，在这一个阶段科研人员提出来很多种有关宽带天线和非频变天线的优秀的理论，并且还将这些理论运用到了相关方面；20世纪90年代是超宽带天线的发展初期，但是直到2002年FCC开放民用的UWB设备使用频段，应用在短距离高速的超宽带天线的研究真正兴盛起来。由于宽带技术的多种优点，研究人员采用了多种方法来拓展天线的带宽，接下来将介绍几种近些年典型的拓展带宽的方法：

1.2.1 降低等效谐振电路Q值

微带天线是一种谐振式天线，它的谐振特性就像是一个高Q值的并联的谐振回路^[2]。对于微带天线，其馈线驻波比不大于ρ的相对带宽的计算公式为：

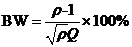（1.1）

这显示出，我们可以通过降低等效谐振电路的Q值来展宽天线的带宽。而降低Q值可以通过增大介质基片厚度^[3]，降低介质基片的相对介电常数等途径来实现。

1.2.2 表面刻槽技术

可以通过在天线的合适的位置刻合适的大小的槽来在一定程度上拓宽天线的带宽。其主要原理是，电流的流向会在刻槽或者刻缝隙之后的微带线上进行弯曲，从而可以达到增加有效电长度的目的，并且同时也可以降低等效电路的品质因数，由此可以在一定程度上拓宽天线的带宽。经过研究人员的实践得知不仅开槽的形状会对天线的性能产生影响，槽所处的位置也会在一定程度上影响天线的性能。

1.2.3 电磁耦合馈电

不同的馈电形式对天线的带宽的大小也起着不同的作用，缝隙耦合馈电系统在微带天线的设计中发挥着很重要的作用，缝隙的尺寸可以根据天线的参数进行设计，不同尺寸大小的缝隙具有不同的作用，利用这种馈电结构可以有效的增大天线的带宽。

1.2.4 分形技术

传统上设计的天线，大多数都是采用的欧式几何的形状，由此大多数天线的尺寸为半波长，而这样就会导致工作在低频段的天线的尺寸很大，工作在高频频段的天线的尺寸的大小也是在半波长左右。而分形结构因其自相似性以及空间填充性，可以实现天线中电流的自相似性以及在天线尺寸改变不大的情况下可以很好的拓宽天线的带宽，因此，将分形理论与天线技术相结合可以实现天线的宽带化的目标。目前，国内外多位研究人员都对此多了深入的研究，并且取得了不错的成绩，例如 Vorya Waladi 等人设计的分形天线可以覆盖到1-30GHz，天线的结构如图1.1所示。国内的研究学者张学勇设计的谢尔宾斯基（Sierpinski）分形天线可以在15mm 20mm 尺寸上实现 2.5-11.1GHz 的超宽带，天线结构如图 1.2所示。近年来 MahdiJalal 等人设计的树状分形结构的天线^[4],Shrivishal等人设计的明科夫斯基(Minkowski)分形结构的天线在将分形理论与天线技术结合的领域取得了不错的进展。

图1.1 Vorya Waladi等人设计的星形分形天线

图1.2 张学勇设计的谢尔宾斯基（Sierpinski）分形天线

目前，运用合适的分形结构，可以很好的提高天线的带宽，并且可以很好的缩小天线的尺寸，虽然现在的技术还不是很成熟，但是将分形技术与天线技术的结合还是会有很大的发展空间。

1.3 本论文的结构安排

通过对宽带技术，分形理论，天线技术的研究，发现分形结构因其自身的特点将其与天线技术相结合可以有效的拓展天线的带宽。由此，全文的主要研究工作是设计两款基于Koch分型结构的宽带天线。首先学习了设计分形天线需要的理论知识，包括分形的种类实现方法以及天线设计中的各个参数计算方法，为设计分形天线做理论基础，在此基础上选择了设计一款基于Koch分女性结构的宽带天线。其次给出了设计天线的具体过程以及完成之后的天线的一些参数。最后给出不同阶的分形结构对天线的影响。

第一章：绪论部分。首先介绍了本论文的研究背景，研究的目的及意义，接下来介绍了国内外有关宽带化的发展状况，详细的介绍了一些典型的宽带技术，并且也简要介绍了分形天线的发展近况。

第二章：本章是本文研究的理论准备部分主要介绍了有关分形理论的知识以及天线的各个特性参数，并且介绍了在本次研究中需要用到的HFSS软件的一些知识点。

第三章：本章节是本文的重点部分。本章首先介绍了能实现Koch分形的迭代函数，并且设计了两款基于Koch分形结构的宽带天线，通过对比加入分形结构之前的天线特性参数与加入分形结构之后的天线的特性参数的对比，来说明分形结构对于天线带宽的作用。

第四章：总结全文。本章主要总结全文的研究并且明确本文的不足点，对未来的有关研究指明方向。

第2章 相关理论概述

2.1 分形基本理论

Mandelbrot在1967年在一篇论文中第一次将局部形态在一定程度上与整体形态相似的结构称为分形，这是分形理论的开端这种相似的性质被称为自相似性。在自然界中还有许多具有自相似特点的东西，例如连续的山脉，不规则的云，树冠，岩石的断裂，虽然这些形态在整体上并没有什么规则可言，但是因其局部与整体具有相似的特点，可以采用一些方法来分析这些形态。之后，Mandelbrot在这基础上进行研究创建了分形几何学。

分形结构拥有两大特点：空间填充性和自相似性^[5]。因这两个特点，将分形理论与天线技术相结合可以有效的拓展天线的带宽，并且可以减小天线的尺寸。由此可见，将分形理论与天线技术相结合的研究对于天线的发展具有重大的意义。

2.2 分形的维数

我们在欧式几何中可以得知，图形的维数都是整数，例如点为一维图形，直线，正方形等为二维图形，立体几何为三维图形等。但是在分形理论中，维数的定义却与几何学中有很大的不同。在分形理论中，维数不仅是整数，也可以是小数，这样就突破了传统几何中对于维数的定义。然而，至今为止，对于分形还没有一个统一的明确的定义，因此测量分形结构的维数的方法也没有得到统一。但是，也是有方法可以根据不同的分形结构测量其维数以反应复杂物体在空间中的存在性，接下来将介绍几种不同的算法：

1. Hausdorff维数

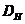
将一个几何结构在某一个方向上放大（或缩小）K倍，则整个结构被放大（或缩小）M倍，则该结构的维数为：

(2.1)

这种方法是测量分形维数的最古老的方法，几乎对于任何几何都适用，但是用这种方法去测量自然界中不规则的物体几乎是不可能的。

(2) 相似维数

如果一个分形对象A（整体）可以划分为N（A,r）个不同大小的子集（局部单元）^[6]，每一个子集以相似比r与原集合相似，则分形集A的相似维数 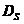定义为：

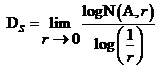(2.2)

相似维数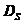主要应用在具有自相似性的几何图形中，人们常常把相似维数为小数的几何称为分形结构，其结果为分形维数。而对于其他的不规则的图形，还有一些其他的方法来计算其维数。

(3) 盒计数维数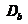

设A是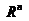空间的任意非空有界子集，对于任何一个rgt;0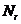，(A)表示用来覆盖A所需边长为r的n维立方体（盒子）的最小数目^[7]。如果存在一个数d，使得当时，有：

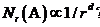(2.3)

那么d称为A的盒计数维数。D通常由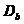表示，经过推理为：

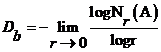(2.4)

以上是毕业论文大纲或资料介绍，该课题完整毕业论文、开题报告、任务书、程序设计、图纸设计等资料请添加微信获取，微信号：bysjorg。

相关图片展示：