基于词典学习和结构聚类的图像去噪毕业论文
2020-04-10 16:14:27
摘 要
图像信号的稀疏性是从何而来的?局部图像模型和非局部图像模型为自然图像的规律性提供了互补的视角,前者试图构造或学习促进稀疏性的基函数字典,后者通过聚类将稀疏性与图像源的自相似性联系起来。论文主要提出了一种统一这两种观点的变分框架,这是一种基于聚类对含噪图像进行稀疏表示从而达到去噪目的的算法。具体的首先用字典学习的方式构建一个冗余字典,然后对含噪图像进行聚类,并通过迭代收缩和L1正则化约束对聚类分块后的图像进行重构,即对相似的的每簇稀疏表示,最终得到去噪图像。研究实验结果显示,在常规纹理图像类上,与最先进的去噪技术BM3D相比,CSR算法处理有了令人信服的改进。PSNR性能的CSR去噪至少是可比的,往往优于其他竞争方案。
关键词:含噪图像;聚类;字典学习;稀疏
Abstract
Where does the sparsity of an image signal come from? Local image model and nonlocal model provides a complementary perspectives regularity of natural images, the former trying to construct or learning to promote sparse dictionary of basis function, the latter by clustering is sparse and self-similarity of image source. In this paper, a variational framework is proposed to unify the two viewpoints, which is an algorithm based on clustering to sparse representation of the image with noise so as to achieve the purpose of de-noising. Specific first use a dictionary to learn ways to build a redundant dictionary, and then clustering in noise image, and through the iterative shrinkage and L1 regularization constraint for image reconstruction after the clustering partition, namely each cluster of similar sparse representation, the denoised image is obtained by the end. The experimental results show that CSR algorithm processing has been improved more convincingly than the most advanced de-noising technology BM3D in the conventional texture image class. PSNR performance CSR de-noising is at least comparable and often superior to other competing solutions.
Key Words: structural clustering,dictionary learning,sparse representation,image denois
目录
第1章 绪论 1
1.1 噪声的由来及影响 1
1.2 关于图像去噪的现有研究 1
第2章 稀疏与聚类相关原理 3
2.1 字典学习 3
2.1.1 K-SVD算法 3
2.2 k-means聚类算法 5
2.3 PCA算法原理 6
第3章 基于字典学习和结构聚类的图像去噪原理 7
3.1算法流程 7
3.2基于聚类的稀疏表示数学原理 8
3.3 算法改进 10
第4章 实验过程及结果分析 11
4.1 实验环境 11
4.2 实验指标 11
4.2.1 结构相似性(SSIM) 11
4.2.2 峰值信噪比(PSNR) 14
4.3 实验流程 14
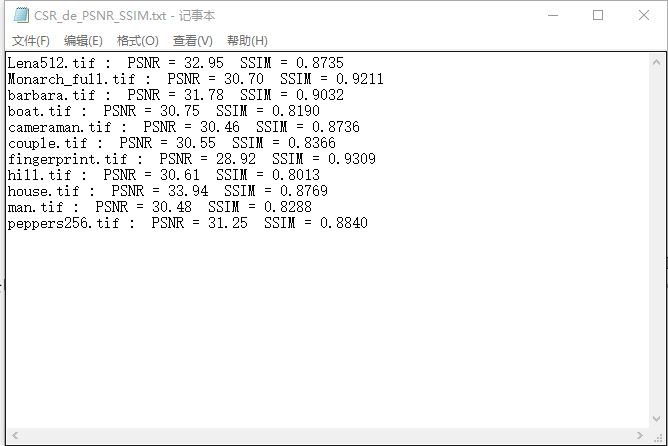
4.4实验结果 16
4.4.1稀疏表示图像 16
4.4.2 CSR算法去噪对比 16
第5章 总结 19
参考文献 20
致谢 21
第1章 绪论
1.1 噪声的由来及影响
从生理学观点来看,凡是妨碍人们工作和生活的因素,都可以被视为噪声。从信号的角度来看,噪声的产生是信号采集、传输以及记录过程中,受到成像设备自身因素和外界环境的影响而产生的。通过定位和界定噪声类型和噪声水平,并且采用相应算法从噪声信号中恢复出真实信号的过程称为去噪。
现实中噪声是随机分布的,只把它定义成一种模型是不准确的。然而,噪声没有办法真正意义上的去除,只能对含噪信号进行优化使之尽可能的减少噪声。所以,去噪严格意义上因该称之为降噪。数字图像在传输的过程中,经常会受到传输通道的影像,比如成像设备和外部环境,从而被加入很多噪声,因此一般将初始得到的图像信号称为含噪图像或噪声图像。噪声会降低图像的清晰度,同时也会对后续图像的分析、压缩和处理等造成影响,所以对图像进行去噪是必不可少的。图像去噪就是一个减少数字图像所含噪声的过程,其目的是解决由于受噪声污染而导致图像质量下降的问题。通过去噪可以有效提高图像信号的信噪比,从而提高图像的质量,更好体现原始图像所携带的信息。
1.2 关于图像去噪的现有研究
因为图像去噪是图像研究领域的一个重要研究方向,研究人员也接连提出了各种去噪的方法。比如传统的空间域和变换域滤波、偏微分方程、基于小波变换、非局部特性的图像去噪方法等。
中值滤波器是我们常用的一种非线性平滑滤波器,在图像去噪上使用中值滤波的原理是:当图像中一点缺失时,用它周围的点的中值来代替。还有一种方法是目前比较热门的研究方法叫小波萎缩法,这种方法可以分为两类:一类是比例萎缩另一类是阀值萎缩。详细介绍一下阀值萎缩方法,先自行定义一个合适的阀值,将小于阀值的系数置零,保留其余的系数,然后对阀值函数进行映射得到估计稀疏。最后通过对估计系数进行反变换运算得到去噪后的图像。比例萎缩法的原理是先判断图像系数含噪的程度,再以此为依据用不同的度量方法,从而确定最终的萎缩比例。近年图像去噪领域的研究热点还包括了基于PDE的图像去噪算法,这种算法已经相当成熟,并在实际生活中得到了应用,它是将噪声图像作为某个非线性PDE的初始条件,再对此PDE进行求解,从而得出不同时刻的解,从而得到滤波结果。Perona和Malik又提出一种滤波方法是基于PDE的非线性扩散滤波,因为线性滤波的方法一直存在着边缘模糊和边缘位置移动等缺点,这种方法的提出能很好的改善这些问题,它是一种非线性各向异性方法。
上面提到的算法都是都是从局部平局滤波的方向上考虑,局部平均滤波就是求解某点的像素时,对其所在领域的所有点像素进行加权平均,从而得到该点的像素。而对参与运算的点的选择标准是它们与需要处理的像素点之间的距离。近年,有研究者发现对图像的去噪处理可以利用图像自身的自相似性。以整体观念重新看待去噪问题。2005年,Baudes等人率先提出了非局部平均图像去噪算法,这种算法利用图像里元素之间的相关性对图像进行去噪处理,这种方法是基于全局处理与之前所提的去噪方法不同,经该算法处理的图像鲁棒性较好并且在图像平滑的基础上能够较好的保留图像细节。在如今的图像去噪算法中NLM算法是去噪效果较好的一种。
NLM算法的出现给了人们新的思路与方向,它在图像去噪领域是里程碑式的,推动了图像去噪理论的发展,之后许多与NLM相关的改进算法被提出,其中比较著名的是K.Dabov等人于2007年提出的块匹配三维协同滤波方法,这种方法利用了局部变换域与非局部平均的优点,将局部与非局部方法相结合,这样既能减少假信号的引入又能较好保留图像的细节,从而使图像的去噪效果更加理想。
图像去噪问题的正则化有两个互补的观点:局部与非局部。局部去噪算法表明:在希尔伯特空间(也称为字典)中,一个信号∈可被分解为一个n维向量集合,可表示为,代表权重向量,的稀疏性可以用其范数(非凸)或计算更易处理的范数来刻画,这种研究涉及了基函数的构造(例如,脊波、轮廓波)和字典的自适应学习(例如:K-SVD,以及随机逼近)。在非局部去噪算法中,自然图像包含自重复模式。利用重叠块本身的相似性可以得出许多非局部图像去噪算法——比如,非局部中值,BM3D,局部学习字典K-LLD(locally learned dictionaries),LSSC(learned simultaneous sparse coding)。在这一系列的算法中,K-SVD算法和BM3D算法一直拥有较高的峰值信噪比(PeakSignaltoNoiseRatio,PNSR)。因此,我们认为联合稀疏性与聚类性可能会更有效的解决图像去噪问题。
依据以上论述,我们提出了基于字典学习和结构聚类的图像去噪算法。基于聚类的稀疏表示是这种算法提供的新模型。CSR模型的基本思想是合并字典学习和结构聚类,就是把局部与非局部稀疏约束归为一类。具体方法是:首先用字典学习的方式构建一个冗余字典,然后对含噪图像进行聚类,并通过迭代收缩和L1正则化约束对聚类分块后的图像进行重构,即对相似的的每簇稀疏表示,最终得到去噪图像。从实验结果来看,本文所提出的CSR算法可以很好的保留图像的结构信息,相比现在比较流行的K-SVD算法和BM3D算法,经该算法处理过的图像的峰值信噪比(PNSR)更高。
第2章 稀疏与聚类相关原理
2.1 字典学习
字典学习又能称为稀疏表示,这里我们将一个只有有限个非零采样点,而其他采样点均为零或者接近零的信号称为稀疏信号。但实际上,真正意义上的稀疏信号很少,我们所碰到的图像基本是非稀疏的,为了方便处理,在这里引入了可压缩信号概念。它的定义是:在不丢失或者能够保留大部分信息的条件下,某一信号经过一系列处理能够变成稀疏信号,即可以证明该信号在某变换域是稀疏的,这种信号就能称为可压缩信号。我们可以利用可压缩信号去逼近原信号。
以下是稀疏性的特点:
⑴不相关性
不相关性指的是含噪图像与真实原始图像之间的不相关性。图像中的有用元素之间往往存在联系,而噪声的分布则是独立的、随机的、离散的。
⑵自适应性
稀疏分解不需要原始图像信号与噪声图像的统计特性,通过信号在过完备字典上分解,用来表示信号基,可以自适应的根据图像信号自身的特点灵活选取[1]。
⑶原子化
利用原子能量的特性对图像信号进行稀疏分解。由此得到大小两类原子,通过它们再分别从时域上提取分布较短的信息成分和分布较长的信息成分。利用过完备原子库的稀疏性表示图像。啊啊啊啊啊啊啊啊啊啊啊啊啊啊啊啊啊啊啊啊啊啊啊啊啊啊啊啊啊啊啊啊啊
字典学习有两个步骤,第一个步骤是构建字典,第二个步骤是利用字典对图像进行稀疏表示[2]。实质上,字典学习实现的就是对大量数据集的降维,字典学习实质上就是要得到图像数据的最本质最简单的特征,就如同字是构成句子的最本质的特征一样,这就是稀疏表示的概念:用尽量少的原子来表示尽可能多的元素的这种思想还有一种优势就是可以提高计算的速度。我们希望在字典里的字尽可能的少的情况下,表示最多的句子,这样的字典最能达到稀疏要求。而在本次实验中我们采用的是K-SVD算法思想来得到冗余字典和稀疏系数。
2.1.1 K-SVD算法
K-SVD算法是一种很经典的字典训练算法,它的大体思路是根据最小误差的原则,对误差项进行奇异值分解,把分解的项中误差最小的作为原子系数和更新的字典原子,最后通过不停的迭代对比最终得到最优化的解,下面是K-SVD字典学习算法的基本流程。
啊啊啊啊啊啊啊啊啊啊啊啊啊啊啊啊啊啊啊啊啊啊啊啊啊啊啊啊啊啊啊啊啊啊啊啊

愤怒地积分卡积分卡拉胶覅时间看了记录科技就离开了基里连科及垃圾那就看
图2.1 K-SVD字典学习算法基本流程
让我们详细推导以下字典构建过程,令,,分别表示字典、训练信号、训练信号的稀疏表示稀疏向量,为N个训练信号的集合,为解向量的集合[3]。从线性组合角度看,K-SVD训练算法的目标方程可表示为:
上面公式中,t代表稀疏表示系数中非零点的最大个数,即表示稀疏系数向量的稀疏程度。从误差逼近角度看,还可以将K-SVD训练算法的目标方程表示为:
上述两式本质上是相同的,只是考虑的问题的角度不同,我们将公式(2.2)作为目标函数。我们用迭代的方式对式子(2.2)进行求解,以得到最优解。我们先假设有一个初始字典D,用匹配追踪、基本匹配追踪、或基追踪等稀疏分解算法求得训练样本在过完备字典上的稀疏表示系数矩阵;反过来再由系数矩阵X,推得进一步优化的字典D。
字典的更新方式是一列一列更新的。先假设已经确定了系数矩阵X和字典D,将要更新字典的第k列,令系数矩阵中相应的第k行为(不同于的第k列的装置),那么可以改写目标函数式中的惩罚项为如下式子:
进的那黑客江湖金口贵很贵吧一个月体育
式中,乘积被分解为K个秩为1的矩阵的和。按照假设其中K-1项是固定的,所剩的一个,也就是要处理的第k个。矩阵代表的是去掉原子的成分在所有N个样本中造成的误差。啊啊啊啊啊啊啊啊啊啊啊啊啊啊啊啊啊啊啊啊啊啊啊啊啊啊啊啊啊啊啊啊啊啊
因为中0的影响,用SVD得到的更新向量中的非零值的位置和数量会和原中非零值位置和数量不同,出现“发散”。
我们可以通过以下方法来解决这样的问题,去掉中所有的0,仅保留非零值,再用SVD更新和时,就不会出现“发散”现象了[4]。
定义集合为用到所有信号集合索引所构成的集合,即的点的索引值。定义为矩阵,它在()处值都为1其他点为0。定义
,,
则三者分别为,,中去掉零输入后的收缩结果,为当前用到原子的样本的集合,为去掉不受原子影响的样本后,如果不考虑在受其影响的样本成分时带来的误差,的长度为,和是矩阵。
此时,最小化式(2.3)得到的解和原解就会有相同的支撑,不会出现“发散”相当于式(2.3)经过一次转化,转化为
将做SVD分解,则,令为的第一列,则为的更新结果。同时,用V的第一列和的乘积更新,在逐列更新完成后用新的字典做稀疏分解,并判断算法是否达到终止条件(终止条件可以是既定的迭代次数或者重构信号和原始信号之间的误差率),以决定迭代是否继续[4]。
2.2 k-means聚类算法
首先先搞懂什么是聚类分析,聚类就是将数据进行分组,尽可能提高组内的相似性,组内的相似性越大,组间差别越大,则聚类的效果就越好。然后再来看看k-means算法,它的计算过程其实非常直观:
先从数据中随机取k个元素,作为k个簇的各自的中心。然后计算剩下的元素到这些中心的距离,将离各自中心最低的点归为一簇,之后再移动之前选取的中心到它现在所处的簇的中心。这是一个流程,之后继续计算比较其他元素到中心的距离,不断更新这k个簇中心点的位置,直到它们的位置稳定下来。
2.3 PCA算法原理
PCA(Principal Component Analysis)是常用的一种分析数据方法做主成分分析,它将原来高维数据线性变换为一组低维且每个维度之间线性无关的数据,这种算法主要用来提取数据的主要成分,并将高维度数据降为低维度数据。虽然降维可以减少计算量,但它往往会导致信息的丢失,这就需要我们借助数据集自身元素之间的相关性,在对数据降维的同时减少丢失信息的损失。下面大致的介绍一下PCA原理。
PCA降维的大致思想是:选取特征明显并且比较重要的信息保留下来。那么如何选取这些特征明显且重要的点就成了关键问题。这里有两个选择标准。首先同一个维度里的点越离散越好。举个例子,假设我们要将二维数据降到一维数据,设有A(1,2),B(2,1)两个点,如果将他们投影到直线y=x上,则两点会重合为一点,这就是所谓的数据丢失。所以我们应该找一条线使两点投影在上面不重合,然后以这条线上的单位向量的模为基重新定义每个点在一维空间上的位置。要尽量避免点在降维时重合,即要求它们尽量离散,可以用方差来描述点的离散程度,方差越大表示自己与平均水平差异越大,就越有个性,降维后数据越能分得开,减少数据丢失的损失。
另一个选择标准是两个维度之间的关联度,关联度越小越好。因为关联度小表示两个维度表征相同信息的量少,最理想的情况两个维度没有关联,关联度为零。关联度可以用协方差来表示,在线性空间内表示为两个维度正交。
现假设我们有m个n维数据,将它排成nm的矩阵X,设,则C是一个对称矩阵,并且我们可以发现矩阵C的对角线分别为各个n维数据方差,其余为各个n维数据之间协方差。这样问题就简化了,我们的目的就是要使得协方差矩阵对角线上的元素从大到小依次从上至下排列,使其余的元素为零。在线性代数里就是将协方差矩阵对角化。
总结一下PCA的算法步骤,设有n条m维的数据集,将它排成m行n列的矩阵,算出矩阵中每一行的均值,再让每一行减去它所对应的均值即零均值化,这样是为了后面更好进行运算。之后求出矩阵的协方差矩阵,再相继求出协方差矩阵的特征值和特征值所对应的特征向量,最后按照特征值大小将其所对应的特征向量从上至下按照行排列成矩阵,取矩阵得前k行组成新的矩阵P,矩阵P就是将原矩阵降到k维后的矩阵数据。啊啊啊啊啊
第3章 基于字典学习和结构聚类的图像去噪原理
3.1算法流程
以下为算法实现的框架:
稀疏表示
构建字典
聚类分块
重构
图3.1 流程图
在这里我们给出了上述CSR去噪算法的贝叶斯解释。在小波阈值化的文献中,稀疏表示与贝叶斯去噪之间的联系已经建立起来。这种联系在过去的十年里对两种理论的发展都是有益的,因为它有助于调和确定性学派和概率学派之间的差异。正则化函数和先验分布在确定性和概率条件下的双重作用,已经证明了变分和贝叶斯图像去噪的等价性。因此,我们认为将上述连接从本地(基于字典的)扩展到非本地(基于集群的)框架是有用的。CSR的基本思想是假设我们可以将K个簇的质心作为稀疏系数的对等隐藏变量。这种想法本质上是为了认识到解决构成(与位置相关)图像信号的不确定性的重要性。因此,我们可以给出下面的最大后验(MAP)估计公式:
以上是毕业论文大纲或资料介绍,该课题完整毕业论文、开题报告、任务书、程序设计、图纸设计等资料请添加微信获取,微信号:bysjorg。
相关图片展示:






课题毕业论文、开题报告、任务书、外文翻译、程序设计、图纸设计等资料可联系客服协助查找。



