摘 要

节能减排一直是世界近几十年来的重要研究课题，随着经济的发展我国对能源的需求与日俱增，这背后隐藏着的是巨大的能源危机，节约能源迫在眉睫。管道运输减阻是节约能源的一个重要途径，克服管道壁面摩擦阻力所做的无用功往往占据了运输总功相当大的一部分。因此减少管壁的摩擦阻力对节能减排意义重大。论文通过对对不同工况下的流场进行仿真模拟，比较凹坑表面和光滑表面的不同流动特性，对凹坑型非光滑表面进行减阻机理研究，并提出改良方案。

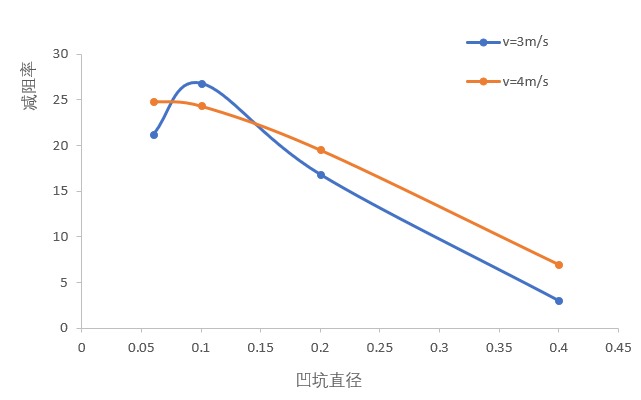
数值计算结果表明：非光滑表面存在压差阻力，但因其粘性摩擦力的减小幅度高于压差阻力带来的负面影响，因此整体表现为减阻特性；凹坑尺寸较小时更容易获得较大的减阻率，当凹坑直径在0.1mm时，在来流速度为3m/s，5m/s和8m/s时减阻率分别为26.8%，24.36%以及31.58%；非光滑表面结构导致边界层增大，减小了速度梯度，进而减小了粘性摩擦力，凹坑内部存在的低速涡流使得粘性摩擦力减小，两个因素共同促使凹坑型非光滑表面呈现出减阻特性。

关键词：非光滑表面；边界层；涡流；数值模拟

Abstract

Energy saving and emission reduction has always been an important research topic in the world in recent decades. With the development of our economy, the demand for energy is increasing, and there is a huge energy crisis behind it, and it is imminent to save energy. The drag reduction of pipelines is an important way to save energy, and the existence of friction resistance greatly reduces the efficiency of energy utilization. Therefore, it is of great practical significance to effectively reduce pipe resistance and improve the efficiency of energy utilization. The paper simulates the flow field under different working conditions and compares the flow characteristics of the turbulent boundary layer on the non-smooth surface and the smooth surface. The drag-reducing mechanism of the non-smooth surface is studied, and an improvement scheme is proposed.

The numerical results show that the non-smooth surface has the pressure difference resistance, but the decrease of the viscous friction force is higher than the negative effect of the pressure difference. Therefore, the overall performance is the drag reduction characteristic. The dent size is easier to get a larger drag reduction rate than the hourly pit size. When the diameter of the concave pit is at 0.1mm, the flow velocity is 3m/s, 5m/s and 8m/s decrease. The resistance rate is 26.8%, 24.36% and 31.58%. The non-smooth surface structure leads to the increase of the boundary layer, the decrease of the velocity gradient and the decrease of the viscous friction. The low velocity eddy current in the pit reduces the viscous friction force, and the two all make the non-smooth surface exhibit the drag reduction characteristic together.

Key Words：Non-smooth surface；Boundary layer；Numerical simulation；vortex

目 录

第1章 绪论 1

1.1 选题背景、目的及意义 1

1.2 国内外研究现状 1

1.2.1 沟槽技术减阻 1

1.2.2 仿生技术减阻 2

1.2.3 减阻剂减阻 3

1.3 论文主要研究内容 3

第2章 非光滑表面模型设计 4

2.1 结构化单元体尺寸选择 4

2.2 计算域模型的建立 4

2.3 计算网格划分 5

2.4 数值模型模拟方法 7

2.4.1 数值模型 7

2.4.2 湍流模型 7

2.4.3 湍流方程 8

2.5 近壁面相关处理 8

2.6 边界条件和初始条件 9

第3章 计算结果与数据分析 11

3.1 模拟思路和减阻评定标准 11

3.1.1 模拟思路 11

3.1.2 减阻评定标准 11

3.2 模拟结果分析 11

3.2.1 凹坑尺寸对减阻率的影响 11

3.2.2 来流速度对减阻率的影响 13

3.2.3 压差阻力与粘性摩擦力 15

3.3 物理量分析 15

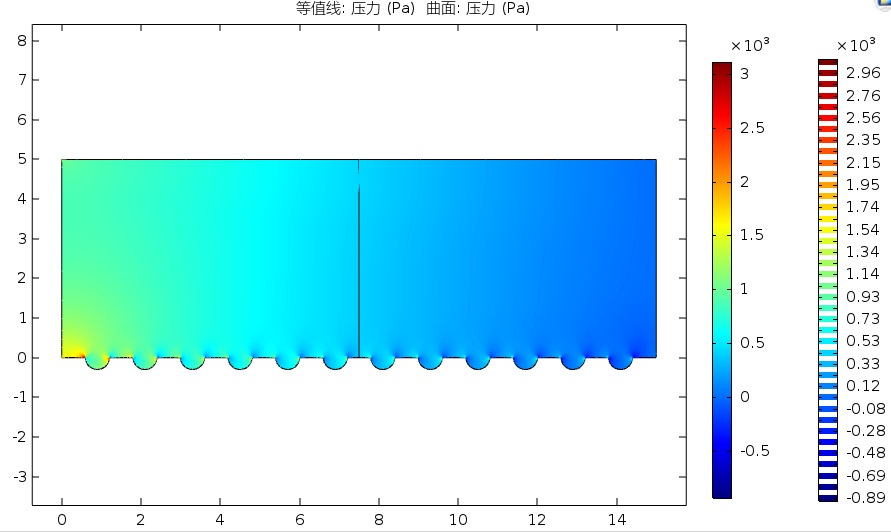
3.3.1 压力分析 15

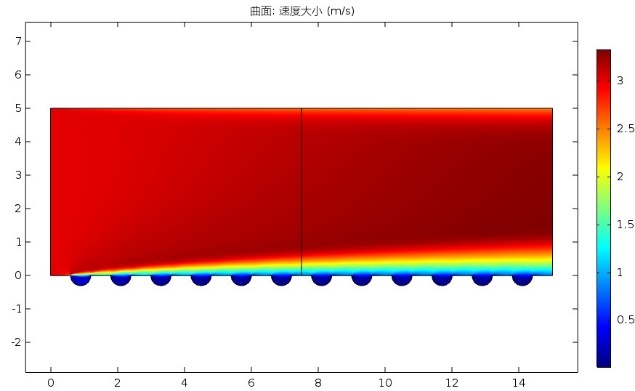
3.3.2 速度分析 16

3.3.3 湍流动能与湍流耗散率 17

3.4 减阻机理分析 17

3.4.1 边界层厚度 17

3.4.2 凹坑结构中存在低速涡流 18

3.5 模型优化 18

第4章 结论与展望 20

4.1 主要结论 20

4.2 后续工作展望 20

参考文献 22

致谢 24

第1章 绪论

1.1 选题背景、目的及意义

节能减排的研究一直是世界近几十年来的研究课题，随着中国经济的迅速发展，我国对能源的需求与日俱增，这背后隐藏着的是巨大的能源危机，我国长期以来面临的人均资源匮乏问题就足以体现这一点。何况目前能源危机遍及全球，节约能源迫在眉睫。

日常生活中，管道的减阻是节约能源的一个重要渠道。管道运输技术大量运用于各行各业如油气储运、消防系统等领域中。而管道壁面摩擦阻力的存在，会使得相当大一部分能量做出无用功——摩擦阻力的存在抑制了流体在管道中的流动，这使得相同运输量下更多的能量会被消耗。在运输工具中，总阻力里有相当大一部分是表面阻力，尤其在长距离的管道运输中，克服表面摩擦阻力所消耗的能量几乎占泵站所提供的二分之一^[1]。面对这随处可见的阻力损失，有效地减少管道表面摩擦阻力，提高能源的利用效率就具有重要的经济价值。

1.2 国内外研究现状

人们对于管道减阻的研究开始于20世纪30年代 ^[2]。起初从宏观感性的角度人们认为表面越光滑阻力越小，但到了60年代，大量的仿生学研究结果表明；许多生物的表面并不是光滑结构，从微观角度看反而是各种非光滑体表。借助仿生学研究结论，通过在研究对象表面布置具有一定几何形状的微型结构以模仿生物表皮构造可达到减阻效果，这种表面称为沟槽表面。自此，作为一种新兴的减阻技术，沟槽结构表面减阻技术逐渐走进了人们的研究领域并得到迅速发展。技术人员以此为发散点，研究各种不同构造的微观表面的减阻效果。目前随着新型材料的发展，人们在多个领域如沟槽表面减阻，仿生学减阻，减阻剂减阻等均取得了丰富的研究成果。

1.2.1 沟槽技术减阻

对于沟槽结构减阻，首先从沟槽与流体方向关系上主要分为纵向（即来流顺沟槽方向流动）和横向（来流跨越沟槽流动）两种。首先纵向有两种理论——Bachert等提出的第二涡群论和突出高度论。对于第二涡群论，Bachert认为沟槽两侧反向旋转的流向涡与尖顶形成的二次涡相互作用，二次涡削弱了与低速条带相联系的流向涡对的强度，抑制了流向涡对在展向聚集低速流体的能力，使得低速条带保留在沟槽内并减少了低速条带的不稳定性从而减小了阻力；至于突出高度论，Bechert等采用黏性流动理论对沟槽的减阻机理进行了分析，阐述了表观起点和突出高度的概念，Walsh等、Gallagher等与Bechert等的观点相似^[3]。目前对于横向的研究工作相对较少，潘家正所做实验表明流体跨过沟槽结构时在谷底形成涡结构，起到滚动轴承的作用。它将流体和壁面之间的滑动摩擦转变为滚动摩擦。此外，肖如亭等所做低粘附功管道的内流减阻研究表明液体与光滑管道内壁间的粘附功大小对内流阻力有影响。他认为当液体的内聚功大于液体和管道接触产生的粘附功时,减阻区和非减阻区都会有内流阻力^[4]。在1980年早期，Walsh等定义了沟槽结构的高度无量纲尺寸h 和间距无量纲尺寸s ，并确立了一种结构尺寸范围，这种结构尺寸范围能较好地达到减阻效果。此外他们提出减阻效果最好的是V型结构表面，减阻率能够达到达８％。王召峰等认为非光滑表面的减阻机理是其在一定程度上削弱了流动附面层的能量脉动 ^[5]。2009年，刘占一等研究了横向布置的沟槽间隔因素对减阻性能的影响，研究结果表明，随着间隔的逐渐增大，减阻效果先上升后下降。胡海豹等研究结果表明沟槽表面增大了层流底层厚度，从实际效果来看这层加厚的层流底层厚度相当于一条低速带，流场中的高速流体与此低速带接触，相当于在流体与壁面间插入了一层润滑剂，即低速带的存在减小了摩擦阻力^[6]。王晋军等也认为层流底层厚度增大后，相同位置的流场流速比原来大，即阻力得到了减小^[7]。2017年，彭倩等的仿真实验表明凹坑型非光滑管道壁面沿程阻力较小，该研究可对管道内壁基于纹理减阻提供一定参考依据^[8]。

1.2.2 仿生技术减阻

对于仿生减阻的研究，是以鲨鱼为突破口。鲨鱼作为海洋霸主，游动十分迅速，尤其是和其他同级别海洋生物相比较而言，所以，鲨鱼的表皮结构一直是研究的热点。对鲨鱼微观表皮的研究表明，鲨鱼皮表面具有顺流动方向的细微的类似圆环形鳞状结构，这与沟槽几何形状本质上是相同的^[9]。Bixler等发现鲨鱼能够迅速在水中移动，且微结构化的肋条覆盖在皮肤上能保持皮肤清洁，这样的肋条有效地减少了皮肤摩擦阻力，还能固定自然发生的湍流旋涡^[14]。目前，许多学者借助流体力学理论对鲨鱼皮微沟槽结构的减阻机理进行了相关研究。Choi等在试验中发现沟槽结构能够降低流体与沟槽内壁的剪切应力，这是因为沟槽的宽度和尺寸间隔很小，流体顺着沟槽方向流动时，垂直于来流方向的涡旋宽度比沟槽间距要大，因此径向涡旋只能与沟槽顶接触。和直接与壁面接触相比，流体由受到面摩擦转换为等同受到线摩擦，摩擦剪切应力明显得到了降低^[10]。Chernyshev和Zayets发现微沟槽结构能够抑制流体的分离，以上几点是鲨鱼皮微沟槽结构能够实现减阻的原因。韩鑫等人复刻出了仿鲨鱼皮结构，最大减阻率高达8.25％。这种由仿生原理延伸出的沟槽结构在军事武器、泳衣、流体机械等方面获得了广泛的应用：和普通鱼雷模型相比，具备条纹沟槽结构的鱼雷模型有更高的减阻效果，其最大减阻幅度约为8％^[11]；北京奥运会上美国著名游泳选手菲尔普斯打破金牌记录时，他所装备的有微沟槽结构的泳衣引起了世人的关注，这种俗称鲨鱼皮泳衣的装备能够获得３％～５％的减阻效果^[10]。2015年Yan Yao等对高雷诺数下的表面涂层结构进行了实验研究，证明了减阻和延缓附聚效应^[15]。此外，西北工业大学胡海豹等人提出了采用准LIGA成形技术制备沟槽表面的方法，用此法在铝合金平板上制备出了沟槽结构平面。

1.2.3 减阻剂减阻

减阻剂的作用机理和上面几种有所不同。减阻剂分子本身具有弹性，在被加入流场时会附着到管壁上，并顺着来流方向被流体微元拉伸，且分子会反作用影响流体微元，将一部分较为混乱的应力转换为顺流动方向的力，从而减少总能量的消耗，起到宏观调控摩擦阻力损失的作用^[12]。美国Conoco公司于1960年前后先后研制成功CDR型减阻剂，并已完成商业化应用^[13]。此外，对减阻剂的研究方向还有添加聚合物以增强减阻效果：Dongjie Liu等对阳离子表面活性剂和非离子分子聚合物混合水溶液进行了测试，发现混合溶液的曲线可分为增强减阻区，稳定减阻区和破坏减阻区^[16]。国内关于减阻剂的研究起步较晚，浙江大学于于1985年研制成功EDR型减阻剂；成都科技大学于1984年研究成功PDR型减阻剂。我国最新的EP系列减阻剂性能已达到国际平均水平。

1.3 论文主要研究内容

一直以来人们不断致力于降低能耗，方法之一就是尽量减少各种运输工具中的表面摩擦阻力。因此，研究发展并改进非光滑表面减阻意义重大。

论文针对输油管道的减阻问题，基于非光滑表面减阻机理和平板边界层理论，将输油管道内表面设计成凹坑型或凸起型非光滑管道壁面，利用计算流体动力学仿真软件COMSOL Multiphysic对输油管道内凹坑表面流场进行模拟仿真，分析其流体阻力特性，探究不同非光滑管道壁面对流体摩擦阻力的影响，分析得出关于非光滑壁面减阻的相关的结论、并提出相关的建议。

第2章 非光滑表面模型设计

2.1 结构化单元体尺寸选择

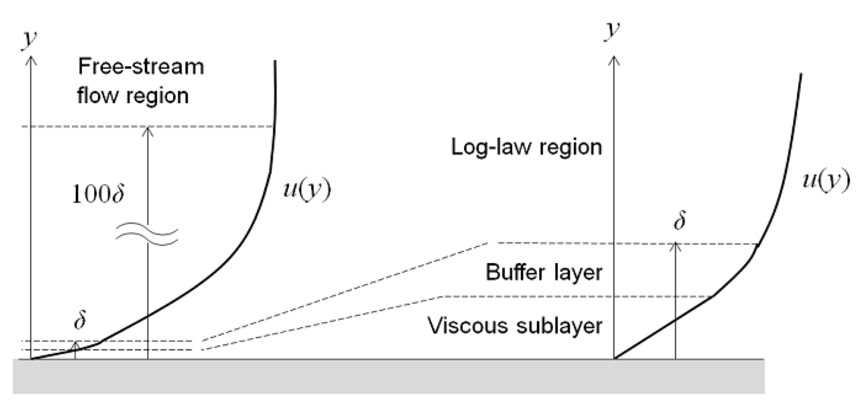
大量的研究表明无论是由于流体的粘性作用引起的摩擦阻力还是由于流体分离引起的压差阻力，他们均和边界层及其厚度有关。通过改变非光滑表面结构来控制边界层厚度会有可能实现减阻，因此非光滑表面尺寸选择和边界层有关。

边界层是指靠近壁面的法相速度梯度较大的一个厚度非常小的薄层。实际应用中一般规定边界层厚度为边界层外边界流体流速达到边界层外部流体流速99％的厚度。在此我们取管道内壁一小块区域，利用公式，通过典型雷诺数来对边界层有一个初始的估计，并据此估算非光滑结构的尺寸。

论文设定计算区域长度为15mm，来流速度范围为3m/s-8m/s。流体以燃油C₁₉H₃₀为研究对象，在20℃时其运动粘性系数υ=3.79×10^-6m²/s，密度ρ=960kg/m³。取V =3m/s。相应雷诺数可用来计算。层流边界层估算公式，湍流边界层估算公式，最大边界层厚度及最小边界层厚度结果如表2.1所示。

表2.1 边界层厚度计算

目前国际上关于凹坑减阻的研究相对于沟槽来说比较少，在结构单元体的尺寸选择上没有系统的理论指导，因此在研究初期我们通过边界层厚度来确定凹坑形态非光滑表面体尺寸，将凹坑深度控制在边界层最小厚度以内。

2.2 计算域模型的建立

COMSOL Multiphysics自带有建模和网格划分功能。它的建模功能十分便捷，不仅支持布尔运算和分割，镜像，阵列等操作，其点抓取功能更优于ICEM等专业前处理软件；在网格划分上，可以实现物理场自动控制网格，也可根据几何形态手动指定边界层等具有特殊要求的网格。

为了便于计算和比较，需要给定光滑表面和凹坑表面相同的初始条件，因此在建模时将光滑表面和非光滑表面相对放置，并使流体流经两表面间隔的区域。这样不仅可以节省计算时间，还能减少计算误差。计算域的长度主要由雷诺数Re来确定。工业上一般取管道流动达到湍流状态的临界雷诺数为4000，根据得到湍流部分估计长度，并据此取板长为7.5mm；为使湍流充分发展，同时考虑网格数量问题，板长取15mm，前7.5mm为层流发展段，计算中只讨论后7.5mm的湍流流动状态。由于将光滑表面与非光滑表面至于同一流场中，为了避免两流场之间相互干扰，应将两表面的间距取合适的值，一般此间距取十倍的湍流边界层厚度，可使上下流场独立互不影响。根据最大边界层厚度的计算值，取高度为5mm。论文重点研究速度与凹坑尺寸对减阻效果的影响和减阻机理，而不对凹坑排列对减阻效果的影响做研究，因此所有模型排列方式为点阵排列，如图2.1所示，图2.2为计算域非光滑表面局部放大图。由于此模型排列具有周期性，因此在此计算域中的流场同样具有周期性。为计算的方便在来流方向上选取一个剖面，并在此二维平面上进行研究分析，如图2.3所示，上下表面为壁面，左侧为入口面，右侧为出口面。

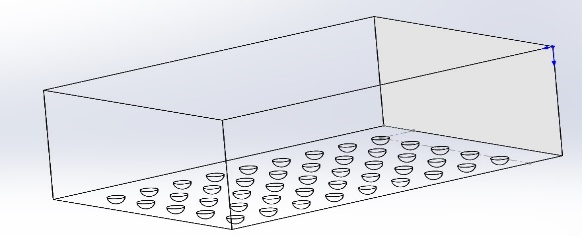
图2.1 计算域模型建立 图2.2 计算域局部放大图

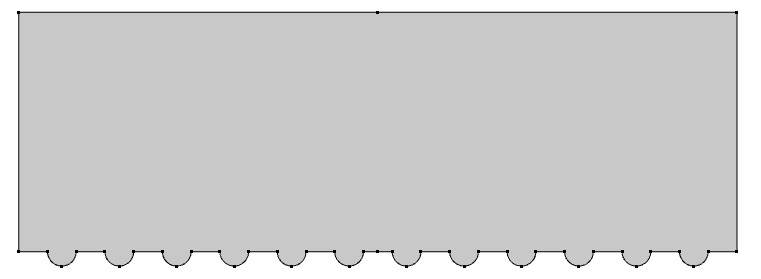
图2.3 二维平面计算域

2.3 计算网格划分

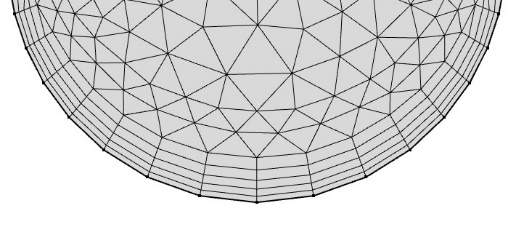
现存有关于平面流场的研究证明近壁面的流体受粘性阻力影响较大，为了保证高度模拟流体在近壁区的流动状态，需要在壁面附近即边界层设置足够密集的网格资源，但此举会增大计算时间和硬件占用空间。综合考虑计算精度和硬件性能，采取靠近壁面处网格分布密集，流场中心网格分布稀疏的划分方法，如图2.3所示。这样既满足了计算精度，也节约了计算时间。光滑边界层样式边界层网格划分样式如图2.4所示，非光滑边界层如图2.5所示。论文设置边界层数为5，边界层拉伸因子为1.2。

网格类型采用自由剖分三角形网格，这种网格能够更快的剖分表面，而且成功率极高。并且只需肉眼观察生成的表面网格，便能轻易发现网格质量的好坏以及特定区域的网格分布。一旦锁定划分质量较差的区域，便可手动修改自由剖分三角形网格，十分直观。

以上是毕业论文大纲或资料介绍，该课题完整毕业论文、开题报告、任务书、程序设计、图纸设计等资料请添加微信获取，微信号：bysjorg。

相关图片展示：