摘 要

船舶在航行过程中，螺旋桨会因船尾伴流场不均匀或者因自身质量不平衡形成周期的弯曲力矩，旋转的横向力矩让推进轴系的旋转轴偏离其静平衡曲线而形成振动并传给全船，回旋振动就此产生，本篇文章主要介绍了国内外对船舶推进轴系回旋振动的研究现状，比较并分析了不同国家船级社对回旋振动的计算规范指南，并介绍了各种回旋振动的计算方法，回旋振动的计算方法目前大体可分为三种（1）有限元法（2）传递矩阵法（Riccati传递矩阵法，myklestad-prohl传递矩阵法，Riccati-Myklestad-Prohlfa传递矩阵法）（3）近似公式法（jasper公式法，panagopulos公式法、Rayleigh 公式法）

利用以上方法均可建立回旋振动模型并计算，但每个方法各有其自身适用范围与计算精度并各有其利弊，例如有限元法目前计算精度最高，与实际情况最吻合。但编程最复杂，在选择计算方法时要综合考虑。

许多因素都会对回旋振动产生影响，如螺旋桨附连水，轴承支承点的选取等等。因此要从这些影响因素入手，考虑减小甚至规避回旋振动保证船舶航行安全。

关键词：回旋振动，推进轴系，影响因素，计算方法

Abstract

During the voyage of the ship, the propeller will form a periodic bending moment due to the uneven wake field of the stern or its own mass imbalance. The rotating transverse moment deviates the axis of rotation of the propulsion shafting from its static equilibrium curve and forms vibration and passes to the whole ship ,which called whirling vibrations. This article mainly introduces the research status of ship propulsion shafting whirling vibration at home and abroad, and compares and analyzes different National Society of Shipbuilding’s guidelines for the calculation of whirling vibrations and the calculation methods for whirling vibrations. The calculation methods can be broadly divided into three types. (1) Finite element method (2) Transfer matrix method (Riccati transfer matrix method, myklestad-prohl transfer matrix method, Riccati-Myklestad-Prohlfa transfer matrix method) (3) Approximate formula method (jasper formula method, panagopulos formula method，Rayleigh formula method)

The above method can be used to establish and calculate the whirling vibration model, but each method has its own application scope and calculation accuracy and has its own advantages and disadvantages. For example, the finite element method currently has the highest calculation accuracy and is most consistent with the actual situation. However,it’s programming is the most complex .so we should consider comprehensively when selecting the calculation method.

Many factors can affect the whirling vibrations, such as the propeller attachment water, the selection of bearing support point, and so on. Therefore, starting from these influencing factors, we should consider how to reduce or even circumvent whirling vibration to ensure the safety of the ship's navigation.

Key words：whirling vibration, propeller shafting system, transfer matrix, calculation method

目 录

第1章 绪论 1

1.1 研究的背景 1

1.2 研究的目的与意义 1

1.3 研究的国内外现状 2

1.4 研究的主要内容 3

第2章 各国船级社回旋振动规范 4

2.1 中国船级社（CCS） 4

2.1.1 计算模型 4

2.1.2 振动方程 5

2.1.3 回旋振动衡准 5

2.2 挪威船级社（DNV） 6

2.3 英国劳式船级社（LR） 6

2.3.1 概述 6

2.3.2 计算 7

2.3.3 测量 7

2.4 美国船级社（ABS） 7

第3章 回旋振动的模型及计算方法 9

3.1 jasper近似公式法 9

3.1.1简化模型 9

3.1.2 固有频率计算 9

3.1.3 临界转速计算 11

3.2 传递矩阵法 11

3.2.1 简化模型 11

3.2.2各类原件的传递矩阵 12

3.2.3传递矩阵MP法 15

3.2.4 改进传递矩阵法（RMP法） 17

3.3 有限元法 19

3.3.1 简介 19

3.3.2 计算模型建立 19

3.4 几种算法的对比 22

第4章 某艇回旋振动计算实例分析 23

4.1 计算数据 23

4.1.1 轴系布置 23

4.1.2 螺旋桨数据： 23

4.1.3 轴承基本参数 24

4.1.4 轴系几何参数 24

4.1.5 计算考虑因素 29

4.2 计算结果 29

4.2.1 轴系计算结果 29

4.2.2 结论 30

第5章 回旋振动计算结果影响因素 31

5.1 影响因素综述 31

5.2 附连水系数对计算结果的影响 31

5.3 轴承刚度对计算结果的影响 33

5.4 轴承支点位置对计算结果的影响 36

5.5 小结 38

第6章 总结与展望 39

6.1 总结 39

6.2 展望 39

参考文献 40

第1章 绪论

1.1 研究的背景

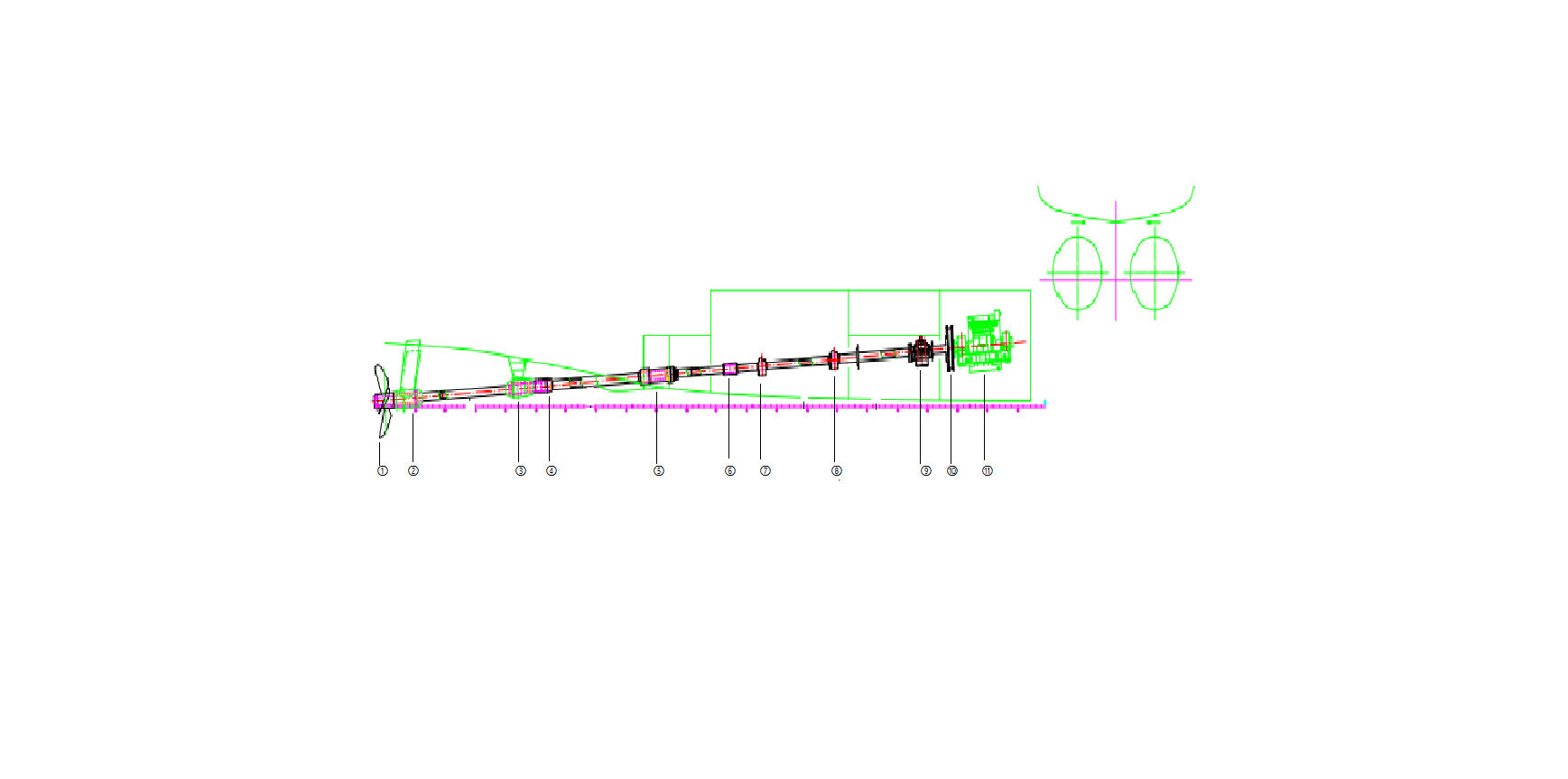
船舶动力装置为船舶供应能量并通过这部分能量来为船舶的航行提供保障，动力装置中轴系是传动设备的关键组成，轴系的作用是传递主机运转产生的功率给螺旋桨并使其产生推力送到船体，形成船舶航行的推动力。由于船舶在海上航行时是一个独立的系统，与陆地隔离，因此一旦发生设备故障或者损坏时不能及时得到外界的支援容易造成船舶损坏或人员伤亡的事故，因此，一定要减少或者避免船舶的各类损坏或者故障的发生，据不完全统计估算，在船舶机械类结构破坏里，轴系造成的故障占比近三成，成为次于主机的第二大问题^[1]，其中轴系的问题主要来源于轴系的振动。由于船舶的高速发展，船舶的尺寸与吨位明显增大，船体各种参数随之变大，因此推进轴系回旋振动的影响对船舶正常运行的影响更加需要重视。螺旋桨不平衡离心力，流体的激振力，螺旋桨偏心重量的重力都会成为推进轴系回旋振动的激振力，国内近年发表的推进轴系相关学术论文数学在逐年增加，也证明了推进轴系振动问题的研究热度在持续上升。

1.2 研究的目的与意义

随着船舶行业的发展 ,船舶各项性能的要求越来越高,其中振动性能的指标要格外引起重视。因为推进轴系振动会造成很多危害，不仅会产生噪音而且会降低传动效率，造成支承轴承配合松动，腐蚀轴承衬套，甚至会发生主轴断裂的事故。目前船舶对轴系的减振要求越发严格，推进轴系振动问题可分为扭转振动、纵向振动与回旋振动。其中，回旋振动会在轴系工作时中心与几何中心有偏差时产生，因为此时转轴不仅以某一速度绕几何中心线旋转，而且会偏离中心发生弯曲。也就是说螺旋桨旋转时候其转轴上存在的横向力矩是产生回旋振动的原因。当螺旋桨工作的伴流场不均匀时，在螺旋桨轴会产生周期性的弯曲力矩^[2]。而轴系转速越高，则回旋振动幅值也将变大。通常情况下，民用船舶的螺旋桨转速较低，此时回旋振动的一阶固有频率一般远远高于工作转速，因此工作转速范围与共振范围没有重叠区间，不会发生共振现象，但对舰艇，尤其是高速船舶，轴系回旋振动很可能产生^[3]。现代船舶船体设计尺寸增大，主参数增大，导致艉部的刚度变小，推进轴系越来越长且支点增多，降低了固有频率，当螺旋桨叶片数增加时，叶频会随之变大导致落共振可能性增大；主机功率的提升使推进轴系传递给船体的推力和力矩变大，由此增大了螺旋桨的激励，因此，回旋振动对现代化船舶的影响举足轻重，推进轴系的回旋振动会给船舶造成许多危害，导致机械故障与船体的振动现象：如，

(1) 尾管后轴承及轴磨损并过热,密封装置失效, 轴承衬套腐蚀，螺旋桨螺帽及支架的松动

(2) 使螺旋桨承受过大的交变应力 ,而非不锈钢轴更会因腐蚀而出现椎体大端龟裂折损等弯曲疲劳破坏，严重时还会导致桨键断裂;

(3) 引起船体尾部结构局部振动 , 使全船振动加剧，降低舒适性并影响船舶安全航行。

因此，现代的船舶尤其是在舰船与速船舶上回旋振动是一定要引起重视的。回旋振动主要发生部位在轴系的尾部，使得测量十分困难，当舰船实际运行中一旦轴系发生故障，排查的难度很大。因此，减轻和规避回旋振动成了重中之重。

1.3 研究的国内外现状

目前已经有很多国家的船级社对回旋振动提出了计算要求与规范，但是对于振动响应都没有提出明确要求。总体来说回旋振动研究还在发展阶段。自二战后“自由轮”等船舶多次发生螺旋桨轴断裂的事故，使人们开始注意到是回旋振动的巨大危害并开始了对回旋振动的研究。希腊学者Panagopulos与英国学者Jasper分别建立了简单的轴系模型，并研究出用于计算回旋振动固有频率的一种估算法，即近似公式法^[3]。在此基础上叶山真治，Smiths等作了进一步的研究。中国开始深入研究轴系回旋振动是在80世纪以后，一些国内学者与教授们分别开发了传递矩阵法计算程序系统，并且计算精度也可以达到国际认可的水平。传递矩阵法是Myklestad和Prohl分别提出的方法经过综合而成。它的优点主要有表达式简单，容易编程，对计算机内存要求低，在传统轴系振动分析中比较常用。至今仍在广泛应用。但当现代船舶轴系变长，轴系支承刚度增大，计算频率变高时，传递矩阵法数值会变得不稳定。

国外船级社和国内相关船舶标准对不同类别的船舶回旋振动都提出了对应的要求与规范，例如，国内相关的船舶标准有:（1）《船舶推进轴系回旋振动计算方法》（CB*/2 336-84）, ,（2）《舰艇结构振动预报和预防措施》(GJB/Z 71-95 )3《舰艇轴系强度计算和横向振动计算规则》（CB/Z 208-83）(3)《钢质海船建造与入级规范(CCS, 2015)》第三分册第三篇第12章。

国外有关的入级规范和指南主要有:（1）《Rules for Building and Classing Steel Vessels (ABS, 2017)》第四册第三章第2节 (2)《Rules and Regulations for the Classificationof Naval Ships CLloyd's Register, 2017 )》第5部分第八章，可见，各国船级社对回旋振动也都分别提出了规范，但对回旋振动的研究仍很欠缺，研究目前仍很落后，远不如纵向振动和扭转振动

1.4 研究的主要内容

本文主要介绍并研究对比了不同国家的船级社对于推进轴系回旋振动的不同规范与指南，并用建立模型的方法将振动计算问题简化，根据不同原件的简化原则将其简化为便于分析的模型，并分析不同的方法，如近似公式法的简化模型以及计算公式，传递矩阵法各元件的矩阵以及计算方法。有限元法对回旋振动的网格模型建立等，并给出衡准，如要规避的转速范围与弯曲应力，本文计算了某艇的回旋振动，其中计算包括了横向振动（h=0）、一次正逆回旋（h=±1）、叶片次正逆回旋（h=±1/5），分析了回旋振动的影响因素，并具体分析每个因素对实船的影响大小并将几个影响因素进行对比，保证船舶能否满足规范安全航行。

第2章 各国船级社回旋振动规范

2.1 中国船级社（CCS）

螺旋桨工作时转轴存在横向力矩会引起回旋振动。当螺旋桨的伴流场不均匀时，螺旋桨轴上会产生周期变化弯曲力，简谐次数为(i=1,2,…),z_p为螺旋桨叶片数^[4]。最重要的简谐次数为。 其次，由螺旋桨或风机不平衡、轴弯曲等造成的激励力，一般为1次简谐。然而，当轴系对它的两个主轴的截面模数不相等时，就会同时产生1次与2次的简谐激励力。当外部激励力传过基座和轴承，回旋振动也有可能产生，且传递后的激励力简谐次数与原激励力的简谐次数相同。

2.1.1 计算模型

将轴系放在空间坐标系里考虑，如图2.1所示，将螺旋桨的静平衡时的中心位置设置为坐标原点 o， 此时x轴负向为船尾方向， y轴负向为右舷方向， z轴负向垂直向下。轴系在y、z方向上的投影如图2.1所示。轴线上任一点振动产生的位移以y、z坐标变化表示。螺旋桨的转角θ_y、θ_z正负向选取按右手定则，即与坐标轴正向方向相同取 。螺旋桨或轴系受力 F_y、 F_z的正负判断与取与坐标轴正方向相同为 ，力矩 M_y、 M_z正负的判断也按右手定则。[5]。

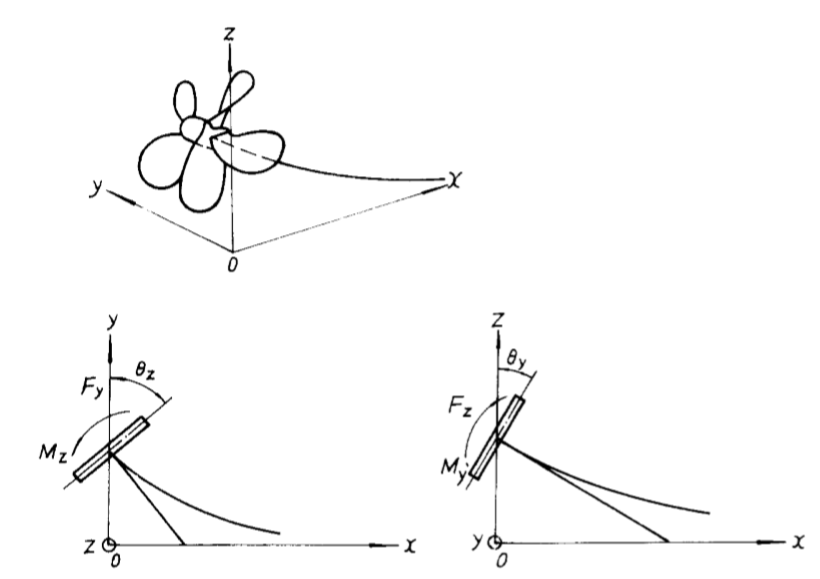
图2.1 推进轴系在y，z方向的投影

2.1.2 振动方程

将螺旋桨简化为一均质薄圆盘，将螺旋桨的质量与转动惯量值加上附连水的影响，将转轴简化为一无质量弹性轴。不计阻尼时，轴系回旋振动的频率方程为：

（2.1）

式中： J_P、J_d 代表螺旋桨极转动惯量和螺旋桨径向转动惯量，kg/m²

是螺旋桨的旋转角速度，rad/s .

是螺旋桨中心处轴在水平,垂直平面的转角，rad

m 是螺旋桨质量，kg；

螺旋桨在单位力下产生的挠度，m/N

螺旋桨在单位力下产生的轴的转角弧度，rad/N

螺旋桨在单位力矩下产生的挠度，m/N

螺旋桨在单位力矩下产生的轴的转角弧度，rad/N；

回旋振动频率，rad/s。

当轴不动时转速为0，这时求得的就是轴系横向振动固有频率，由频率方程可知，回旋振动固有频率与m都有关，但这些影响因素中只有螺旋桨角速度是可变的，其他因素在轴系设计时已经被确定。也就是说，轴系旋转的角速度是主要改变轴系回旋振动的固有频率的参数，造成这一特点的原因是螺旋桨惯性力矩的大小随角速度不同而变化。

2.1.3 回旋振动衡准

a)应规避的转速范围：低速柴油机轴系1次正回旋共振转速一般应在1.2以上；叶片次正回旋共振转速要避免落在（0.85-1）n_e范围区间内； 对细长跨距轴系，在常用转速（0.85-1.0）n_e或使用转速应避开叶片次正回旋共振。气垫船的一次正回旋临界转速不应在（0.8-1.2）n_e范围内^[6]。

b)应限制的弯曲应力:如在常用转速或附近出现叶片次正回旋共振，但按实测值及振型推算的弯曲应力不超过下列范围，则认为符合要求：（1）对用键安装螺旋桨的螺旋桨轴，其锥部前端的弯曲应力为70N/mm2；（2）对用法兰或套合安装螺旋桨的螺旋桨轴，其锥部前端的弯曲应力为100N/mm2。上述应力应包括螺旋桨重力的影响。

2.2 挪威船级社（DNV）

用于推进，动力换向和操纵的所有旋转轴系，无论是何种驱动方式，除了功率少于200 kW的辅助设备以下标准均可适用。在轴的设计过程中可能会要求横向振动计算。特别是具有大轴承轴径比的轴，大多数轴承具有较大重量的螺旋桨，后轴灵活支撑典型的双螺杆设计中艉轴灵活支撑，包括大惯量无艉轴承支撑，无弯曲刚度的齿联轴器的计算。回旋计算的最低限度计算应包括相关振动模式的固有频率和振型。在不确定或重要参数可变的情况下，参数的变化应囊括在分析中。

       指导性说明：重要但不确定的参数如尾部尾管轴承的刚度，产生的轴承载荷位置，长度上的轴承载荷分布（如果用分布式轴承反作用法计算），螺旋桨上的附连水等，应在其可能范围和固有频率内变化作为相应的图表呈现。并且螺旋桨附连水的计算要被表示出来。

与轴速共振（一阶正回旋旋转）和运转速度范围，根据指导性说明，分离余量至少应为操作转速范围的20％。：例如：一个系统低速20 rpm时，转速上限100 rpm时不应该有16到120 rpm范围内的一阶正向旋转，除非证实共振不会造成有害响应，否则应避免在较高的运行速度范围内由螺旋桨叶片引起共振，参见指导说明，指导性说明：标准基于全面的评估，并且应避免在最大转速的80％以上产生共振。可能会有例外情况：如果螺旋桨是主要的激励源，并且轴系前端有共振，则对于被轴承很多的长轴系不会容易被发现。轴承的设计要有合适的阻尼，例如，高轴承长径比与弹性振动模式相结合，可使高转速时产生可接受的共振响应。计算结果应以固有频率数值和图形的形式呈现。例如以坎贝尔图形式来显示。

2.3 英国劳式船级社（LR）

2.3.1 概述

对于所有主推进轴系系统,船东的目标是确保横向振动特性是在船舶的整个转速范围内达到令人满意的程度。船东应提交整个船体外侧或装有万向轴的轴系的横向振动特性计算报告。

2.3.2计算

计算要考虑到轴承，油膜（如适用）和结构动态刚度，船东提交的内容是调查所有临界可能导致会在速度范围内产生显着的振幅的临界速度的激励频率，并指示整个轴系中的相对挠度和弯曲力矩。计算系统的固有频率应与轴旋转次数和螺旋桨叶片通过频率进行比较。 如果安装了万向轴，则还应考虑轴的二阶简谐激励力。根据要求，只要提供证据表明类似动力装置具有满足要求的实船应用时也可以不需要计算要求。

2.3.3 测量

如果计算表明在主机转速±20％的范围内有明显的横向振动响应的可能性。 为了确定对受限速度范围的需要，可能需要使用适当的公认技术进行测量，以从轴系获取测量数据。测量方法应适合于所使用的机械布置和振动模式。当需要测量时，应提前提交详细的计划书。

2.4 美国船级社（ABS）

美国船级社认为，船舶的振动指标对船舶可居住性，安全性和功能性有重要影响，因此要使船舶的振动限制在可接受水平的目标。由于螺旋桨的激励，主推进机械的振动趋于严重。需要格外注意主推进机械的振动，主推进机械的振动标准应由制造商提供。否则，当关于振动标准的数据不可用时，建议将以下标准作为参考。ANSI S2.27（2002）和SNAME T＆R 2-29A（2004）提供了关于主推进机械振动限制的指导原则。振动限值是根据宽频带有多个频率分量（标称值从1到1000 Hz）提供的。 推力轴承（和用于齿轮传动的大齿轮轮毂）的纵向振动均方根，应小于5mm/s。 对于推力轴承以外的其他推进机械部件，不包括发动机，螺旋桨和轴系后部，其纵向振动均方根应小于13 mm/s。对于尾管和线轴轴承，横向振动有效值应小于7mm/s。对于直接柴油发动机（1000马力以上，与轴系连接的中低速柴油机），轴承的振动极限为13mm/s，发动机顶部的回旋振动极限为18mm/s，对于高速柴油发动机（低于1000马力），轴承和发动机顶部的回旋振动应该小于13mm/s。对于1Hz至 5Hz的每个峰值响应分量（垂直方向，横向或纵向方向），可接受的加速度范围是低于126 mm/s²，如果高于285 mm/s²将造成船员不适，建议位移低于1.0mm，损伤可能高于2.0 mm，对于5Hz及以上峰值响应分量（横向或纵向），建议速度低于30mm/s，并且损伤可能高于60mm/s。值得注意的是，上述简单的振动极限不适用于所有具有不同结构船的局部结构振动标准。例如，对于特殊结构诸如有桅杆的软结构，由于振动引起的实际应力水平通常较小，导致1.0mm或2.0mm的振动极限可能过小。另一方面，在固定端部的局部加强板的情况下，1.0mm或2.0mm的振动限制可能偏大。因此，根据船舶规格，特定局部结构的振动限值的应用可能会有所不同。

回旋振动测量时则应在船尾管的轴进行，也可选其他的测量点，测量将在整个船舶的正常工作时进行。为了消除可能的错误，应在轴旋转时候记录一阶信号来检查轴的横向跳动。并且对此进行相应的校正。

第3章 回旋振动的模型及计算方法

3.1 jasper近似公式法

3.1.1 简化模型

将实际轴系简化为一二支承的悬臂梁，二支承为轴系尾端的后二个轴承，按刚性点支承处理，考虑轴段分布质量影响。见图３.１。由于螺旋桨悬臂端的作用，离螺旋桨最近的轴承支承点Ａ₁位置要考虑支承材料和具体结构后确定，若不能获取准确数据时，可按经验取距轴承衬后端面１／３～１／４轴承衬长度处，另一轴承支承点Ａ₂取轴承衬长度中点处。选取的两个支承点的距离l₂与螺旋桨悬臂的长度l₁是由轴段实际长度经过转化后的当量长度^[7]。当量直径取值与螺旋桨轴的直径值大小相等。当量长度按公式3.1计算。

以上是毕业论文大纲或资料介绍，该课题完整毕业论文、开题报告、任务书、程序设计、图纸设计等资料请添加微信获取，微信号：bysjorg。

相关图片展示：