摘 要

本文借助MATLAB软件，首先针对时延估计使用广义互相关法和函数自相关的希尔伯特变换法估算在已知几何关系的麦克风阵列情况下的时延，再通过几何关系确定声源位置。对两种时延估计算法进行了比较。所得结果对于麦克风阵列定位声源具有重要的意义。论文主要研究了广义互相关法和希尔伯特差值法，在高噪声低混响环境下，对时延估计准确性。

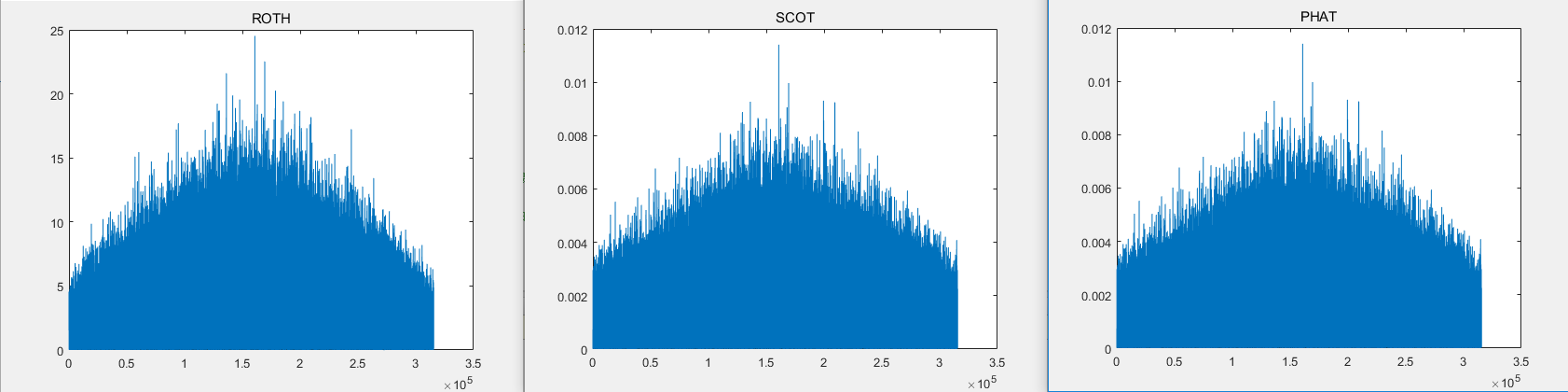
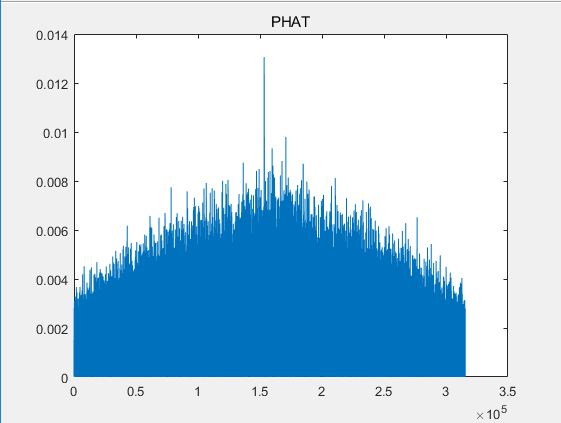
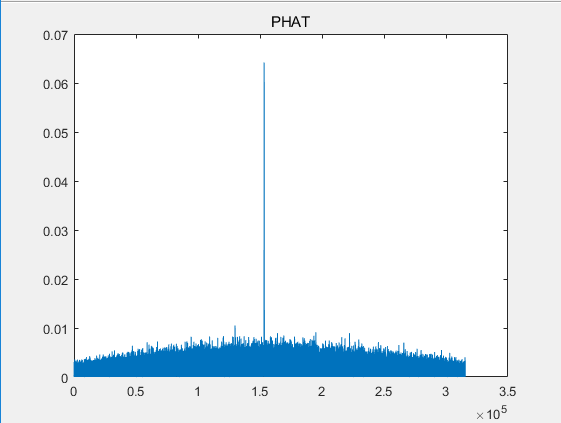
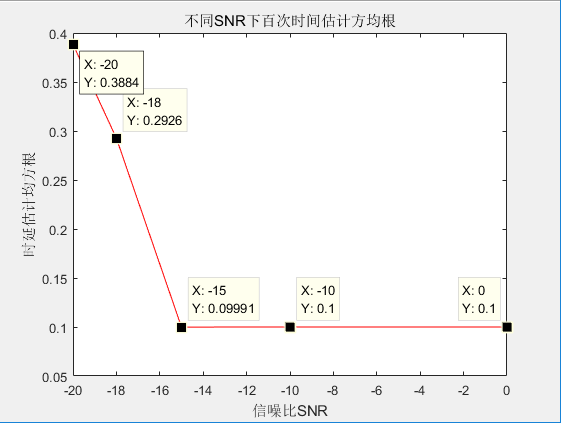
结果表明：采用PHAT广义加权因子的广义互相关时延估计法，在高噪环境下，时延估计准确度高于ROTH和SCOT因子。而希尔伯特差值法相对来说比广义互相关法更好适应高噪环境。

同时，对研究了麦克风阵列的阵列结构对其接受声场信息的影响，选取了十字阵列这一简单低廉，却很好收集声场信息的阵列结构。对十字麦克风阵列的定位性能进行了研究，并进行了仿真时延和误差分析。

关键词：MATLAB；声源定位技术；麦克风阵列；广义互相关

Abstract

In this paper, with MATLAB software, the Hilbert transform method for time delay estimation using the generalized cross-correlation method and function autocorrelation is used to estimate the delay in the case of a microphone array with a known geometric relationship, and the position of the sound source is determined by the geometric relationship. Two time delay estimation algorithms are compared. The results obtained are of great significance for the microphone array positioning sound source. The paper mainly studies the generalized cross-correlation method and Hilbert's difference method, and the accuracy of time delay estimation under high noise and low reverberation environment.

The results show that the generalized cross-correlation time-delay estimation method using PHAT generalized weighting factor can achieve higher time-delay estimation accuracy than ROTH and SCOT factors in high-noise environment. The Hilbert's difference method is relatively better than the generalized cross-correlation method to adapt to a high-noise environment.

At the same time, we studied the effect of the array structure of the microphone array on the received sound field information, and chose a cross array which is a simple and inexpensive array structure with good collection of sound field information. The positioning performance of the cross microphone array was studied, and simulation delay and error analysis were performed.

Keywords: MATLAB； sound source localization; microphone array; generalized cross correlation.

目录

第一章 绪论 1

1.1 研究背景和意义 1

1.2本文研究内容 1

1.3 论文结构 2

第二章麦克风阵列声源定位算法基础硏究 3

2.１声音理论分析 3

2.1.1 声音传播物理量 3

2.1.2声波传播模型 3

2.2麦克风阵列技术信号处理的特点 4

2.3 本章小结 5

第三章 时延估计算法及其仿真分析 6

3.1基本互相关时延估计 6

3.2其他算法及其介绍 7

3.2.1广义相位谱时延估计 7

3.2.2 自适应时延估计 7

3.3 广义互相关法 7

3.3.1 理论分析与算法设计 7

3.3.2 仿真与结果 9

3.3.3 结果分析 13

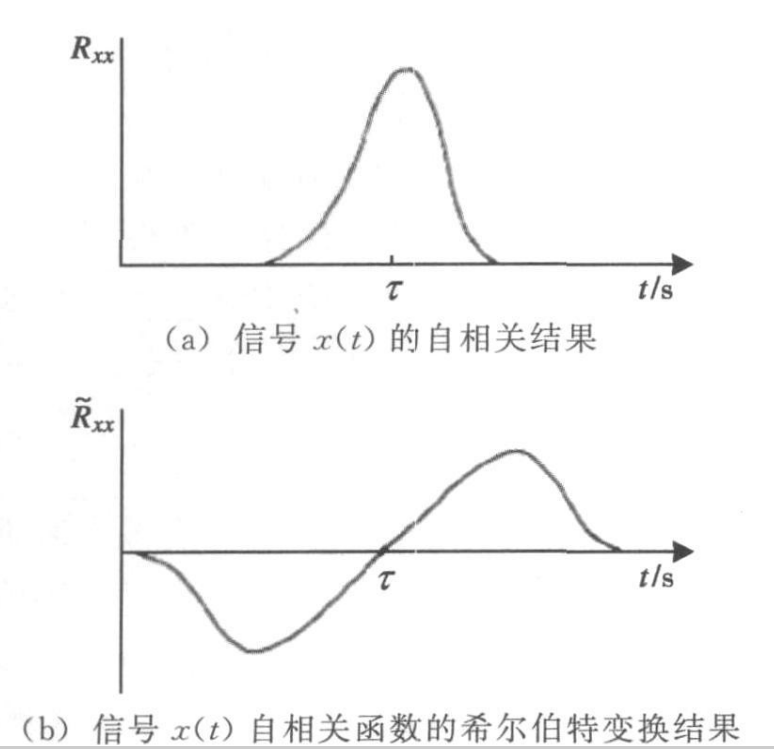
3.3基于希尔伯特变换的时延估计算法 13

3.3.1 算法原理与程序设计 13

3.3.2 仿真结果与分析 15

3.4 广义互相关法与希尔伯特差值法比较分析 16

3.5 本章小结 18

第四章 基于时延估计的十字麦克风阵列声源定位算法 19

4.1 基于十字麦克风阵列的定位算法 19

4.2 基于时延估计的十字阵麦克风的定位算法仿真分析 21

4.2.1 仿真算法设计 21

4.2.2 仿真结果与分析 21

4.3 本章小结 24

第五章 总结与展望 25

5.1 总结 25

5.2 展望 25

参考文献 26

致谢 27

绪论

研究背景和意义

在近代飞速发展的诸多技术中技术，信息处理技术得到了前所未有的突破。定位技术，尤其是声源定位技术技术在各行各业的无数领域中有着重要作用。声源定位技术的研究，无论是在国内还是国外，都越来越受到关注。声源定位技术在军事领域和民用领域都得到了广泛的应用，如在军事领域，声源定位系统可以对低空飞机、火炮等发声目标定位，是对雷达定位系统的补充，且声源定位系统自身不产生声波，具有很强的隐蔽性；在民用领域，视频会议系统中可以采用传声器阵列对说话人进行定向，突出说话人的信号，抑制背景杂音，并可以控制摄像机自动转向发言人 ^[1]。

无论是国内还是国外，基于麦克风阵列声源定位技术都得到了足够的重视。但国内由于研究较晚，许多技术只是拥有一些理论，少数工程应用也不值一提。但无论从硬件和软件哪一方面来说，我国，仍有不短地路要走

基于麦克风阵列的声源定位技术是指通过麦克风阵列对声音信号进行采样，通过信号处理得到声源到达阵列的波达方向，再结合声源和阵列结构之间的关系，得到一个或者多个声源的位置信息，为人们更好地利用声音提供帮助。相比传统的雷达定位技术，麦克风阵列声源定位技术具有隐蔽性好、不易受干扰等优势，应用前景广阔^[2]。

1.2本文研究内容

基于时延估计的声源定位技术是一种双步定位，首先接收声源信号，并通过一系列算法确定每个阵元接收到的时间差，以估计声源信号的方位角和距原点距离。目前，声源定位技术主要采用麦克风阵列来接收声场的信息。 因此，在麦克风阵列特征已知的情况下，即阵列的几何形状，阵元分布等，可以通过获得到达时间的差异，可以精确地计算声源相对于麦克风的方位角坐标。 此中时延估计算法，由于制作成本低廉，容易实现而且运算量极少，能够很好地估计实时声源坐标。 但由于定位时使用的是估计值，会造成累计误差，而且不可消除。 另外，麦克风对于噪声和场景混响的接受，也会干扰时间延迟估计的准确性，这将增加最终位置估计的误差。 而且，在多个声源的情况下，声源之间的相互干扰会干扰时间延迟的估计，因此这种方法不适用于多源估计。 但其性价比与在大多数场景下的精准度仍旧使他广泛应用于各种声源定位系统。^[4]。

本文针对基于时延的定位技术做了以下工作：

（1）对语音信号处理，麦克风的不同阵列对时延估计和定位估计的影响进行分析。研究了声学的背景知识，研究了多种时延估计方法。

（2）研究了基于希尔伯特变换的时延估计算法和广义互相关时延估计算法，并对两种算法进行了对比分析。并在MATLAB环境下进了一系列的仿真分析。最后详细研究了由十字麦克风阵列结构的几何定位方法，并进行了仿真分析。



1.3 论文结构

第一章，系统分析了基于麦克风阵列的声源定位算法的背景知识，国内外研究现状，项目的研究意义以及自身的研究工作。

第二章，研究了声学的背景知识，分析了麦克风接受阵列的特点。采用了十字阵麦克风阵列，对基于此阵列的定位算法分析。

第三章，对基于广义互相关时延估计算法和基于希尔伯特变换的时延估计法。讨论了互相关法和其改进型，并对两种算法进行研究，使用MATLAB对其进行仿真分析。对结果进行分析比较。

第四章，设计基于十字阵列的麦克风定位算法，并使用第三章的算法得出时延，并进行仿真测试，分析误差。

第六章，结论与展望。对本文的工作总结，和对今后研究方向进行了展望，同时给出了文中的一些问题和缺陷，并给出了出现某一部分问题和缺陷的原因，分析了解决的方法。

第二章麦克风阵列声源定位算法基础硏究

2.１声音理论分析

语音信号，作为发声器官这一发声速度相对而言缓慢的声源发出的非平稳信号，我们通常将其短时(10 ms~30 ms)信号认为是平稳信号。平稳信号是多数语音处理的前提条件。在传统阵列信号处理中，有许多与语音信号处理不同的地方，因此了解阵列模型特点，声音传播特点是有必要的。

2.1.1 声音传播物理量

（1）声压

声压指的是在某种介质中传播时，使介质振动产生的压强该变量。若是在气体介质中传播，声波的变化会导致振动变化，以致介质密度的变化，也会导致压强的改变。在麦克风阵列接收声波信号时，由于振动介质与麦克风接收部分的压强变化，会导致一部分的接受噪声。声压用Ｐ表示，在国际单位制中，单位是帕斯卡，用Pa表示。

( 2 ) 声速

声速是声音介质中传播的速度。由于声波只能在介质中传播，介质又受周围环境，如温度和湿度等多方面的影响。所以声速在不同的环境下不尽相同，而我们则通常只考虑空气这种介质中声波的传播，空气中声速的为：

 (2.1)

其中，T为温度，单位^oC。

2.1.2声波传播模型

声波沿波线（或射线）传播，将某一时刻声波振动传播到各点组成的曲面称为波阵面，其中，拥有相位相同的曲面称为相。

根据几何特征，声源可分为点源，线源和面源。

（1）点声源以球面波形式辐射声波。当声源几何尺寸远小于声波波长，且声压与此时距声源距离成反比，就可以将其在其远点视为点声源。

（2）线声源

线声源在远场场景中通常被看作由多个点声源组合形成的线性声源。他们以近乎圆柱形的波形向外辐射声波

（3）面声源：

表面声源是具有辐射声能的平面声源，并且辐射声能对表面的影响在任何地方都是相等的。

2.2麦克风阵列技术信号处理的特点

麦克风阵列是以一定几何方式排列与空间中，用以准确获取空间中的声源信号的多个麦克风。麦克风阵列拥有较强的空间选择性，根据处理算法的不同，可以实现声信号的采集，检测，追踪以及一些其他进阶功能。当麦克风阵列的组成阵列不同时，可以采集的声信号的信息越多，如今主要的形式由线性一维阵列，十字，三角等二维阵列以及球形，螺旋形等三位阵列。不同算法匹配以合适的阵列可以在一定程度上提升算法的性能，如简化运算量，提升精确度等等

麦克风阵列信号处理基于阵列信号处理，所以在很多方面，麦克风阵列的信号处理借鉴了阵列信号处理但。麦克风阵列一般处理的是未经调制的信号，阵元之间时延和相位差与信号频率变化有很大的关联，而且麦克风阵列处理的一般都是平稳或准平稳的，而自然界中，或者说人体发声器官发出的一般都是短时平稳信号，所以在处理这些信号时，短时都是必要的条件。当处理的声源是移动的声源时，麦克风阵列处理难度非常大，一般无法处理。

在麦克风阵列处理和其他信号处理技术中，噪声永远是一个避不开的问题。麦克风阵列处理中，一般有如下几种噪声：①高斯噪声；②非高斯噪声，可能与信号源无关，也可能有关；③混响噪声，主要是经过环境周围阻挡物如墙壁等多次反射后形成的反射波，混响是麦克风处理的一大难点，而且它显著降低了语音信号的质量。

由于一维线性麦克风阵列的定位范围受到限制，因此可能仅在阵列的前方定位一个扇形区域或半空间区域，并且不可能执行全方位定位。 所以采用二维平面阵列。二维平面阵列的定位算法较为复杂，因为阵列的空间结构发生了改变，获取的信号的变多且相对差异变大，使得处理的难度增加，但也扩大了测量范围。常见的阵列有T字形，Y字形，圆形，十字型，这些阵列有着各自的集合特点，匹配合适的算法，能够处理更多的信息。而且，二维麦克风阵列可以弥补在一维平面阵列中定位盲区的缺点，并且可以给出声源的空间三维信息。

所以，在本文中采用了，二维阵列中的十字阵，用来估算三维位置信息。

2.3 本章小结

本章详细介绍了声音，声波的有关知识，模型和物理量。对麦克风阵列技术做了研究，介绍了二维阵列的的优点并在通用性，经济性的前提下，选择了性价比最高的十字阵麦克风阵列作为本文使用的模型。

第三章 时延估计算法及其仿真分析

在常用的几种声源定位算法中，基于时延估计的声源定位算法

运算量小，性价比高，硬件要求简单，而且适用于许多不同的场景

基于时延估计的声源定位算法主要由两部分组成： 时延估计和声源定位算法。 在具有已知几何关系的麦克风阵列的情况下，首先估计每个麦克风元素处的源信号到达之间的时间差。然后通过已知的麦克风阵列几何信息，我们可以计算出的参数信息源位置。

本章主要讨论基本互相关时延和由其改进而来的广义互相关基于希尔伯特变换的时延估计法。

3.1基本互相关时延估计

基本互相关时延估计方法是利用不同麦克风接收同一声源信号具有一定的相关性, 通过参考信号和回波信号互相关函数的峰值估计时间延迟^[5]，假设接收信号 x(n)和y(n)满足下列关系 :

(3.1)

其中s(t)为参考信号；y(t)为 x(t)的时延信号；τ为时延差；和 分别为观测噪声, 它们在统计上相互独立并且与信号无关。。则两麦克风接收到的信号和和的互相关函数就可表示为：

式中，为信号之间的互功率谱。

由相关函数的性质可得，在取得其最大值时，两个信号的相关性最大，声源到达两个麦克风之间的时间延迟可由此换算出来。

利用基本互相关方法求时延虽然简单，但是有两个条件在现实环境下大概率无法得到：一、在基本互相关中要求得到信号的先验知识，而且必须保证噪声之间互不相关，噪声与信号之间也不相关。但可惜的是现实环境下基本是不可能符合的；第二；严格意义上的统计平均也是无法达到的。

3.2其他算法及其介绍

3.2.1广义相位谱时延估计

由（3.2）可知，相关函数和其功率谱密度函数互为傅立叶变换，所以信号的相似性可以通过时域中的相关函数进行比较。 时延 D 通过傅立叶变换在频域上表现为功率谱密度函数的相位函数, ( f) =- 2fD, 从而通过相位函数对进行时延估计。 同广义相关加权函数一样, 也可以用相位加权函数在频域对相位函数进行加权, 从而形成了广义相位谱时延估计算法。但也需要信号和噪声的统计先验知识, 并且仅适用于无噪声干扰或不相关高斯噪声干扰的情况^[6]。

3.2.2 自适应时延估计

由3.1节知，基本互相关的不足在于需要信号和噪声的先验知识。为了克服这一缺陷，自适应时延估计算法被B.Widrow 提出。在没有信号和噪声的统计先验知识的情况下, 这种算法能通过调整自身参数，来追踪时变的时延。然而，当滤波器阶数高时, 存在计算量巨大，且收敛速度缓慢等缺点。它是牺牲了估计速度，放弃了对噪声和信号统计先验知识要求。

目前，有两种改进的自适应延迟估计算法：

( 1) ETDE 及可变步长法LMS算法通过迭代权向量将延迟问题转换为滤波器的参数估计问题。当信噪比SNR的环境下，我们需要增加更加高阶的滤波器。由此，ETDE被提出，改进了自适应滤波器，使之更适合低噪环境。随后为了解决时变环境下估计速度的降低问题，ETDEG算法被提出：它在其基础上，使用一个参数—功率因子来适应不断变化的信噪比同时使运算速度极大的提高。

( 2) 基于拉格朗日插值的ETDE及其相关时延估计方法的时延估：对具有已知中心频率的欠采样窄带信号执行时延估计。为此，拉格朗日延迟滤波器的CAF被截断sinc函数延迟滤波器的自适应系数因子所替代。也就是说，形成了混合修改的拉格朗日直接延迟估计算法。 它可以在较宽的频率范围内使用较小阶自适应滤波器进行延迟估计，并且可以实现无偏估计。

3.3 广义互相关法

3.3.1 理论分析与算法设计

由于基本互相关算法存在很多缺陷，噪声和混响环境中相关函数的最大峰值减弱，出现多个峰值，造成峰值检测的困难，往往使估计产生比较大的偏差，这就需要对观测信号作特殊处理。通过对互相关函数进行加窗平滑, 实现信号的预白化处理, 能够提高信噪比,提高时延估计精度^[8]。

由（3.2）可知，相关函数和功率谱密度函数是一对傅立叶变换对，若是在频域利用不同的加权函数，如SCOT、ROTH等：

为频域加权函数。

对功率谱密度函数进行加权，以相对较高的信噪比增加麦克风接收的有效信号的频率成分。 通过抑制低SNR的频率分量，噪声功率被有效地抑制，使互相关函数峰值更为明显。由于在无噪情况下两路信号之间的时延处是其峰值，所以锐化的也是时延处峰值。再将频域信号转换到时域，得到广义互相关函数，找到相关函数的峰值位置，即为信号之间的相对时延^[9]。

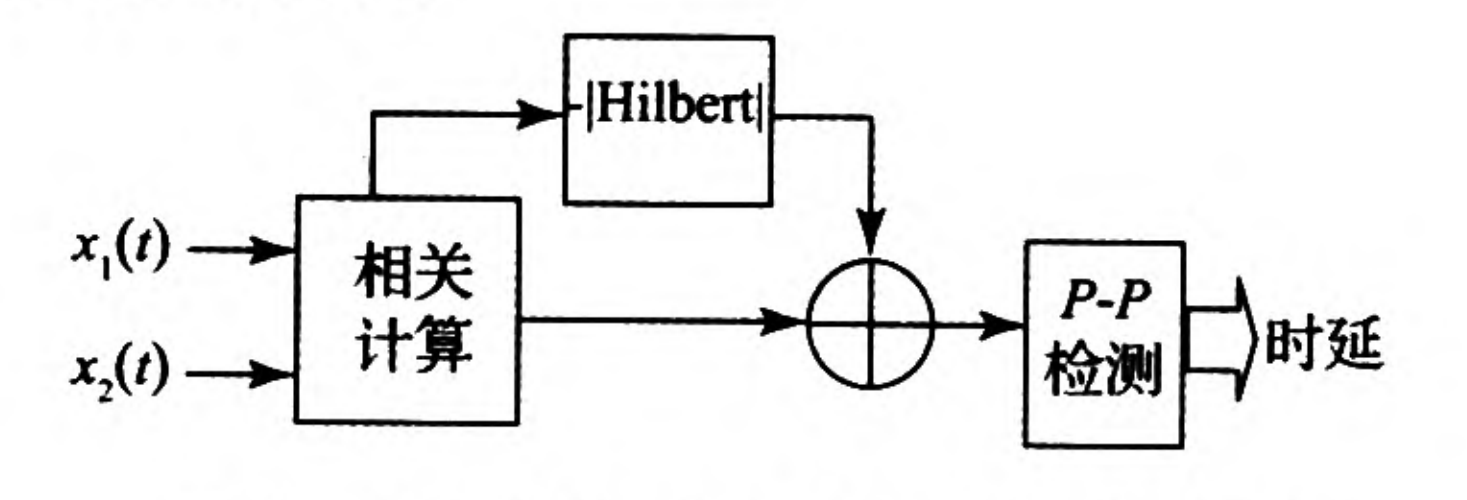
广义互相关函数法：首先对两路信号求快速傅里叶变换（FFT），对其中一路 FFT 数据取共轭，然后计算两路信号之间的互功率谱，利用频域加权函数对信号滤波，突出响应信号部分的频谱成分，抑制噪声部分的频谱，再通过FFT反变到时域，锐化相关函数在时延处的峰值，提高时延估计的性能^[10]，使互相关函数使两个信号之间的时间延迟的峰值更明显。

以上是毕业论文大纲或资料介绍，该课题完整毕业论文、开题报告、任务书、程序设计、图纸设计等资料请添加微信获取，微信号：bysjorg。

相关图片展示：