基于二分网的公共物品博弈模型及仿真毕业论文
2020-04-11 18:02:22
摘 要
本文基于多智能体仿真平台Repast和二分网络,结合复杂网络和演化博弈理论,对公共物品博弈进行建模,并对复杂网络基础上的演化博弈进行研究。二分网是复杂网络中一种重要的网络表现形式。现实世界中的许多网络,都呈现出自然的二分结构,例如:听众和音乐组别,足球队和队员,科学家和论文等等。二分网由两种类型的节点构成,边只在不同类型的节点间存在。自然和社会中一系列的合作网络,都可以描述为合作主体和合作事务构成的二分网。二分网具有普遍性,已经成为复杂网络研究的重要对象。公共物品博弈的主要内容是,假设有一个公共的账户,参与者每个人可以投资任意数目的金额。公共的账户和每个投资人的关系的结构符合一种二分网络的结构。当公共账户中的金额累积到一定数目后,它会乘上一定的系数实现投资增值,然后总收益平均分配给每一名参与投资该账户的人。参与人投资得越多,个人收益相应越多。如果参与人都不投资,那么公共账户中就一分钱没有,大家也就一无所获。社会中的很多问题都可以用公共物品博弈来描述。因此,研究基于二分网络的公共物品博弈是很有意义的。
关键词:Repast;公共物品博弈;二分网;复杂网络;演化博弈
Abstract
This article is based on multi-agent simulation platform Repast and binary network, combined with complex network and evolutionary game theory, the public goods game model, and study of complex networks based on evolutionary game.Binary network is an important network representation in complex network.Many networks in the real world have natural dichotomies, such as listeners and music groups, football teams and players, scientists and papers.Binary network consists of two types of nodes, and edges exist only between different types of nodes.A series of cooperative networks in nature and society can be described as a binary network of cooperative subjects and cooperative affairs.Binary network is universal and has become an important object of complex network research.The main content of the public goods game is that if there is a public account, each participant can invest any amount of money.The structure of public accounts and the relationship between each investor fits into a binary network.When the amount of money in a public account accumulates to a certain amount, it will multiply it by a certain coefficient to realize the investment appreciation, and then the total income will be distributed equally to everyone who participates in the account.The more participants invest, the more they earn.If the participants do not invest, there is nothing in the public accounts and nothing for everyone.Many problems in society can be described by the game of public goods.Therefore, it is meaningful to study the game of public goods based on the binary network.
Key words: Repast;Public goods game;Binary network;Complex networks;Evolutionary game
目录
摘要 I
Abstract II
目录 1
第1章 绪论 1
第2章 博弈论知识概述 2
2.1经典博弈论、博弈模型与纳什均衡 2
2.2从经典博弈到演化博弈 3
第3章 复杂网络上的博弈 5
3.1规则网络上的博弈 5
3.2小世界网络上的博弈 7
3.3无标度网络上的博弈 8
3.4自适应网络上的博弈 10
第4章 二分网络 11
4.1 二分网络简介 11
4.2研究方法与演化模型 11
第5章 模型设计及仿真分析 13
5.1模型设计 13
5.1.1 Repast仿真平台简介 13
5.1.2 模型的实现 13
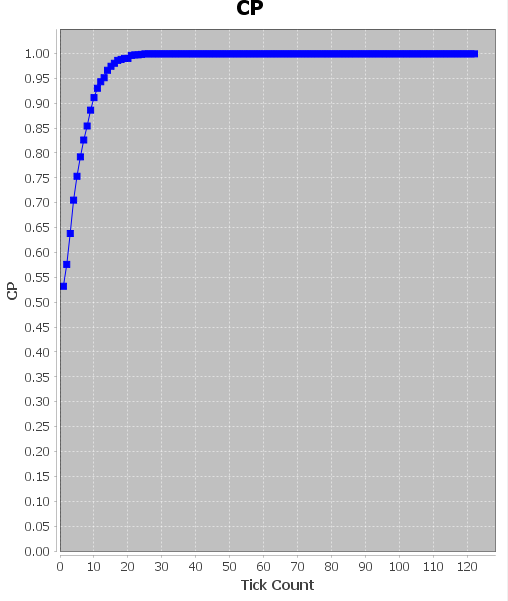
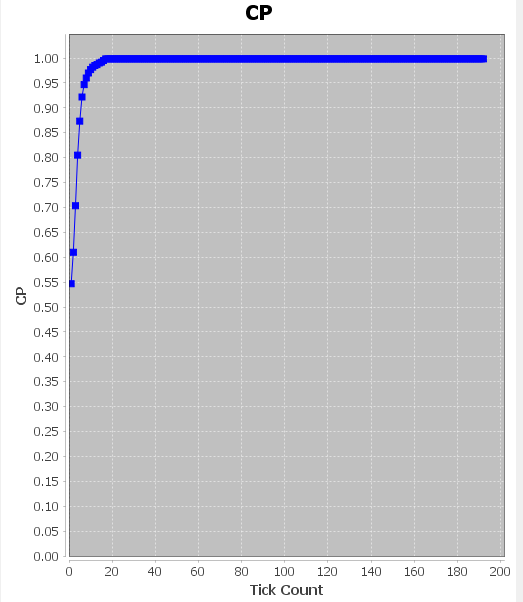
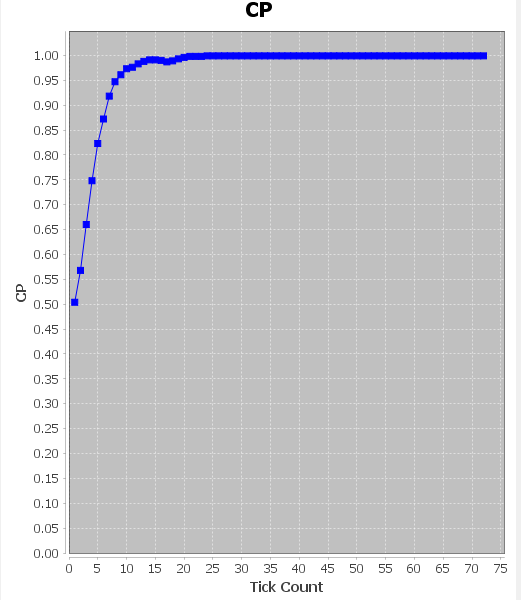
5.2仿真分析 13
第6章 总结与展望 16
参考文献 17
附录 18
致谢 21
第1章 绪论
目前博弈论已被人们广泛的运用在经济学、生物学、社会学等多个学科之中,而复杂网络理论是研究复杂系统强大的工具,将博弈理论与复杂网络理论相结合,已成为研究复杂系统的一个新热点。在不同的学科中人们都提出了分别适用的博弈模型,如囚徒困境博弈、胆小鬼博弈、雪堆博弈、协调博弈以及最后通牒博弈等,并且都得到了比较好的符合实际的模拟结果[1]。
囚徒困境博弈模型是一个比较典型的博弈模型,也是人们研究得很早的模型之一,它的内容虽然简单,但是可以比较好地帮助人们理解博弈的过程,因此很受人们的重视。但是博弈结果显示,最后总是背叛策略占领着统治地位,而这与实际的情况并不能很好的符合,在现实生活中很多事情都需要人们共同的合作才能得到完美的解决。所以人们为了研究合作行为而考虑了更多的模型,其中之一就是在博弈中加入重复博弈。因为实际生活中人与人之间并是只接触一次,而是可能经过不久的时间又会接触,如果他们再一次进行博弈时,先前的博弈结果就会很影响他们第二次对策略的选择。通过这样的研究人们发现,合作也可以在重复的双人博弈中存在。
同时,因为实际生活中往往不仅是两人之间的博弈,而是许多人之间的博弈,因此有必要将囚徒困境模型发展成为一个多人博弈的模型,这就是目前人们研究的新的网络模型之一——公共物品博弈模型。在公共物品博弈中,有一个公共账户,多个参与者每个人可以给这个账户进行投资,每个人可以投资任意数目的金额。公共的账户和每个投资人的关系的结构符合一种二分网络的结构。投资结束后,经过一段时间,公共账户中的钱会乘上一定的系数实现投资的增值,然后总收益会平均分配给每一名参与投资该账户的人。公共账户中的钱越多,大家所获得的收益相应越多。若是参与人每个人都不投资,那么公共账户中就一分钱没有,大家也就一无所获[11]。社会中的很多问题都可以用公共物品博弈来描述。
由于复杂网络给人们提供了一个研究由许多子系统组成的具有一定拓扑结构的复杂系统的一种很好的途径,于是人们很自然地想到将博弈模型与复杂网络进行结合,希望可以通过这样的研究模式来解释实际生活中的一些自然现象,比如一些昆虫的集体行为,人们在某些社会活动中的一些共同的行为,这些研究也已经取得了很多有意义的结果。
本文在了解博弈理论与二分网络相关知识的基础上,基于Repast平台研究了二分网络中的公共物品博弈的问题,探究投影网络中整体的合作水平的变化趋势,以及公共物品博弈参数对整体合作水平的影响。
第2章 博弈论知识概述
2.1经典博弈论、博弈模型与纳什均衡
博弈理论,又被称为对策论,主要研究对象交互作用下的个体行为的演化。博弈论是应用数学的一个分支,已经被广泛应用于生物、经济、政治、信息等众多的学科。在交互作用下,个体所获取的收益(payoff)不仅与它自身所采取的策略(strategy)有关,也于其他个体所采取的策略有关。19世纪科学家冯诺依曼和摩根斯坦发表了他们的著作《博弈论和经济行为》。该书就论证了这一观点。这本书被认为是经典博弈论诞生的标志,奠定了经典博弈理论的基础。
一般一个博弈由以下四个部分所组成:(1)博弈参与者。在一个博弈中至少有两个个体参与博弈。(2)博弈者所选择的策略集。博弈的策略集由参与博弈的所有参与者所有可选择的策略所构成。(3)博弈方的收益。当博弈参与者选择好自己的策略后,其所获取的收益由收益矩阵中的相应的元素来决定。(4)策略演化。在多轮博弈的过程中,博弈的个体遵从自身收益最大化的原则,来进行策略的调整。20世纪中叶,美国科学家约翰·纳什曾提出了经典博弈论中的一个重要的概念——纳什(Nash)均衡,这个概念的主要内容是对于两人或多人博弈,个体的策略演化会逐步趋向于一个均衡态,在这个均衡态下全部的个体会同时采取“纳什均衡策略”,没有个体可以通过单方面改变策略而获得更高的收益。下面我们以常见的囚徒困境博弈和雪堆博弈为例简要地阐述一下纳什均衡的意义。
囚徒困境博弈:两个共谋犯罪的人甲和乙共同作案,被捕后被隔离开审问,甲和乙两人不能互相交换信息。如果两个人都拒绝揭发同伴的罪行,将会因为证据不足,两人将会被轻判一年有期徒刑;为此,警方设计了一个机制:如果甲揭发乙的罪行,而乙不供认甲的罪行,则揭发者甲将会因为立功被无罪释放,而乙将会因为拒不认罪被重判十年有期徒刑;如果甲和乙都揭发对方罪行,则双方会因为证据确凿均被判刑八年。在这种机制下,自私的个体会如何选择?不难得到,如果甲选择拒绝揭发乙的罪行,即选择与乙“合作”(cooperate-C),则乙的最佳做法是揭发甲的罪行——意味着“背叛”(defect-D)对方,这是因为此时选择揭发甲,乙自身就无罪释放了;如果对方甲选择揭发自己的罪行,则乙的最佳做法也是选择揭发甲的罪行,因为此时坐八年牢总比坐十年要划算的多。对于两人的博弈,收益矩阵元通常用(R、S、T、P)来表示, 如果二个人相互合作则都获得较大收益R,如果相互背叛则都获得较小收益P,而一方合作一方背叛,则背叛者获得最高收益T,而合作者会获得最低收益S,即满足关系:Tgt;Rgt;Pgt;S,此外2Rgt;T S,即两个人相互合作可以获得集体最高收益。由此可见,无论对方采取何种策略,选择背叛对于自己来说都是最佳的策略,所以理性的个体最终都会处于相互背叛的状态。当甲和乙都相互背叛时,没有人愿意先改变白己的策略(单方面改变策略只能使得自身的收益更低),这种相互背叛的状态(D,D)就是系统的纳什均衡态。
雪堆博弈:在一个风雪交加的晚上,两个人开车相向而行,被一个雪堆所阻拦,如图2.1所示。白色和灰色分别表示合作策略与背叛策略。与囚徒困境博弈不同,对于雪堆博弈,收益矩阵元满足关系:Tgt;Rgt;Sgt;P。
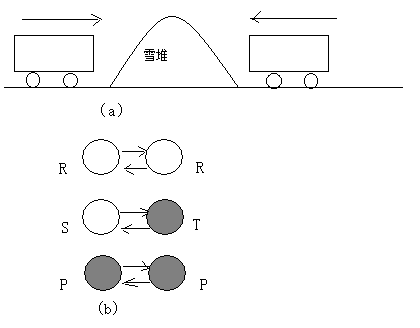
图2.1 雪堆博弈
假设铲除这个雪堆使道路通畅需要付出的代价量化为c,如果道路通畅则带给每个人的好处量化为b(bgt;c)。如果两人一齐动手铲雪,则他们的收益均量化为R=b-c/2(分别承担劳动量c/2);如果只有一个人下车铲雪,虽然两人都可以通行,但是背叛者逃避了劳动,它的收益量化为T=b,而合作者的收益量化为S=b-c,如果两人都选择不合作,则两个人都会因为雪堆的存在而无法通行,其收益量化为P=0。那么,理性个体的最佳的选择是什么呢? 如果对方下车铲雪,则自己的最佳策略是呆在车中,因为这样可以获得最大收益。如果对方选择背叛策略(呆在车中),那么另一方的最佳策略是下车铲雪(因为道路通畅带来的收益b-c好于呆在车中的收益0);由此可见,与囚徒困境博弈模型有些不同,在雪堆博弈中存在两个纳什均衡态:(C,D)和(D,C)。
2.2从经典博弈到演化博弈
在经典博弈理论中,所有个体是被假定是超理性的(即所有个体都知道其他个体也是理性的,并且会按照理性行事),且个体对收益矩阵元的信息完全了解。在这种机制下,所有个体最终都会采取纳什均衡策略。从上面的囚徒困境博弈和雪堆博弈可以知道,这种个体的超理性会导致集体的非理性(因为相互合作时集体收益最大)。一般而言,在复杂的环境中个体没有充分的条件去选择最佳的策略以获得最大的收益。在这种情况下,个体一般都会根据其所掌握的局部信息,做出令其“满意”的决策,这种选择过程表明个体的理性是有限的。演化博弈理论着重研究有限理性的个体如何在重复博弈过程中,通过自适应的学习来实现自身收益最大化的问题。
十九世纪六十年代,Lewontin最先尝试应用博弈论的思想解决生物科学中的问题。Smith和Prices于1973年在Nature上发表了他们的著名论文动物冲突的逻辑,该文采用博弈理论的思想从个体选择的角度阐释了动物间的争斗为什么总是一场有限的战争,而不会造成非常严重的伤害。这是博弈论的思想第一次被正式地应用于生物科学中。从经典博弈论发展到演化博弈论,有三个关键性概念的内涵发生了转变。
第一个是策略的内涵转变。在经典博弈论中博弈个体所采取的各种不同行为构成策略集。在生物系统中,则由不同类型的物种本身组成“策略集”(例如策略可以由物种的表型特征(phenotype)所体现,不同的策略则对应于表型的变异)。个体在继承其父辈的表型特征时可能产生某些变异(mutation),这些变异决定了它在与其他个体的相互竞争中的生存优劣程度,或者是适应度(fitness)的大小。通常,个体的适应度可以由其后代的数目来进行量化。这样,经典博弈论中超理性的观点在演化博弈论中被科学家达尔文的“适者生存”的观点所替代。那些不使用“理性”策略的个体会在漫长的演化过程中逐步趋于灭绝。
以上是毕业论文大纲或资料介绍,该课题完整毕业论文、开题报告、任务书、程序设计、图纸设计等资料请添加微信获取,微信号:bysjorg。
相关图片展示:
课题毕业论文、开题报告、任务书、外文翻译、程序设计、图纸设计等资料可联系客服协助查找。



