基于量子云计算平台的量子算法研究毕业论文
2020-04-12 09:04:51
摘 要
由于量子计算在大整数分解等问题上展现出的强大计算能力,研究者们一方面致力于研发实现通用量子计算机的实验技术,另一方面致力于设计出新型量子算法。近年来用于量子计算的超导量子芯片取得一系列突破性进展,量子云平台也随之应运而生,其中最典型的当属IBM量子云平台。
本文详细介绍了量子计算理论中量子比特、量子门、量子线路等基本概念,以及若干常见量子算法的理论;同时,还从硬件和软件两方面对IBM量子云平台的架构,进行了简要的说明。为了测试IBM量子云平台的性能,本文使用IBM开发的量子信息软件工具QISKit编写量子程序演示了Deutsch-Jozsa算法、Grover算法、Phase estimation以及Shor算法。最后,本文还探索了一个有趣的问题,即如何实现多比特GHZ态,文中共给出了Complete graph、Single expansion、Multiple expansion这三种实现方法。这些方法都能用来实现n-qubit GHZ态,但Single expansion极大受限于量子芯片的拓扑结构,Multiple expansion使得量子线路过于复杂而产生较大误差,因此,Single expansion是最好的选择。
关键词:量子算法;量子云平台;GHZ态;
Abstract
Due to the powerful computational capabilities of quantum computing in some problems, such as the factorization of large integers, researchers have been dedicated to develop experimental techniques for implementation of general-purpose computers, or to design new quantum algorithms. Quantum cloud platforms have emerged after a series of breakthroughs in superconducting quantum computing chips in recent years. The most typical platform is the IBM Quantum Cloud.
This paper introduces the basic concepts of quantum computing, including quantum bits, quantum gates, and quantum circuits, and several important quantum algorithms in details. Then, it will explain the architecture of IBM Quantum Cloud Platform briefly, in both hardware and software aspects. To test the performance of IBM Quantum Cloud Platform, QISKit, developed by IBM, is used to write quantum programs to demonstrate Deutsch-Jozsa algorithm, Grover’s algorithm, phase estimation and Shor’s algorithm. Finally, an interesting problem is explored, namely how to achieve multi-bit GHZ states. Three methods, i.e. complete graph, single expansion, and multiple expansion are given. These methods can all be used to achieve n-qubit GHZ states, however, the complete graph is greatly limited by the quantum chip’s topological structure, and the multiple expansion generates a very complicated quantum circuit and gets a large error. Therefore, the single expansion is the best choice.
Key Words:quantum algorithm;quantum cloud platform;GHZ state
目 录
第1章 引 言 1
1.1 研究背景及意义 1
1.2 研究现状 2
第2章 量子计算基础知识 5
2.1 量子比特 5
2.2 量子门 6
2.2.1 单量子门 6
2.2.2 CNOT量子门 7
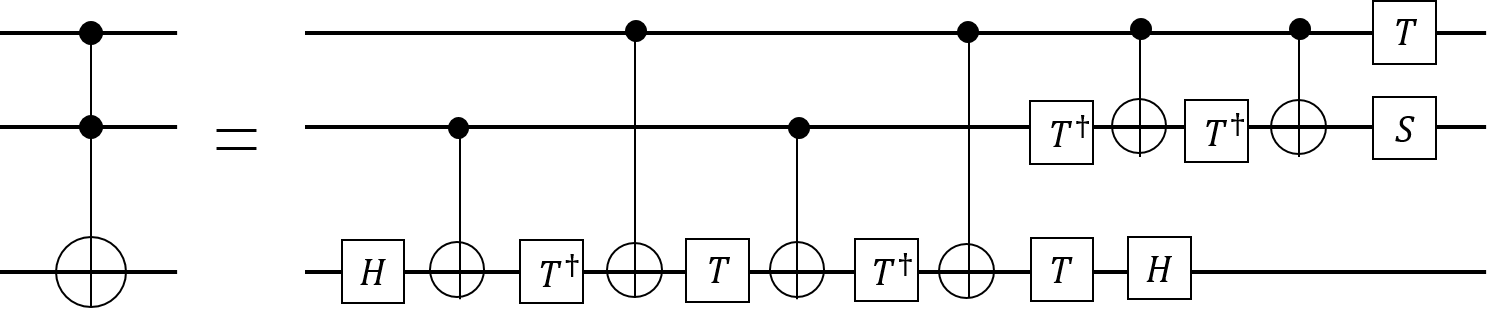
2.2.3 复合量子门 8
2.3 量子线路 9
第3章 量子计算云平台 11
3.1硬件部分 11
3.1.1 量子比特 11
3.1.2 量子门 13
3.1.3 读出 14
3.1.4 ibmqx4的具体信息 14
3.2 软件部分 16
第4章 常见量子算法及其实现 18
4.1 Deutsch-Jozsa算法 18
4.1.1 算法描述 18
4.1.2 算法实现 21
4.2 Grover算法 22
4.2.1 算法描述 22
4.2.2 算法实现 23
4.3 QFT和Phase estimation 24
4.3.1 算法描述 24
4.3.2 算法实现 27
4.4 Shor算法 28
4.4.1 算法描述 28
4.4.2 算法实现 29
第5章 GHZ态的探索研究 31
5.1 初衷与目标 31
5.2 实现方法 31
5.2.1 Complete graph 31
5.2.2 Single expansion 33
5.2.3 Multiple expansion 34
5.3 测试与分析 35
第6章 总结与展望 38
参考文献 39
附 录 42
致 谢 48
第1章 引 言
1.1 研究背景及意义
量子力学自二十世纪首次被提出以来,一直是当代物理学中最重要的基础理论之一,它不仅成功解释了许多经典物理所无法解释的物理现象,同时也推动了新兴学科和技术的诞生。得益于半导体物理学和半导体加工技术的迅猛发展,计算机从最初的真空晶体管,发展到现如今的大规模集成电路,其功能和性能已发生了翻天覆地的变化。然而,由于量子极限和散热等[1]问题无法彻底得到解决,芯片的集成规模难以进一步得到提高,经典计算机的运算能力也随之受到限制。因此,基于量子力学原理的量子计算机,有望从根本上解决上述的问题,极大地提升计算机的运算能力。本章将首先回顾量子计算机的研究概况,然后介绍量子计算的基础理论知识。

图1.1[2] NFS(数域筛法)和 Shor算法用于大整数因式分解
量子力学与经典力学最大的区别是量子叠加和量子纠缠。所谓的量子计算机,正是利用这些原理来实现量子并行运算,那么具体来说,与经典计算机相比,量子计算机有哪些优势呢?首先来看看大整数因式分解:给定一个整数Q,已知它是2个素数的乘积,要找出这2个素数。应用数学家Shor在1994年提出著名的Shor算法,在量子计算机上运行Shor算法可以有效地解决大整数因式分解,其复杂度随着问题的规模多项式增长。而到目前为止,对于大整数因式分解还没有找到有效的经典算法,最好的算法(即数域筛法,NFS)其复杂度也是随着问题的规模指数增长[3]。图1.1给出了Shor算法和NFS分解L位数所需时间的对比,从中可以看出:随着L的逐渐增大,Shor算法所需时间远小于NFS,这表明量子算法在此问题上有着巨大的优势。更重要的是,目前广泛使用的 RSA密钥系统的理论基础正是大整数因式分解的复杂性,Shor算法的提出使其安全性受到挑战。
另一个重要的例子是无序数据库量子搜索算法,该算法由Grover于1996年提出。现在考虑旅行商问题:假设我们有一张包含很多城市的地图,如何找到一条经过所有城市的最短路径。一个简单的办法是搜索所有可能的路径,从中找到最短的一条路径。如果我们总共有N条可能的路径,经典算法的搜索复杂度是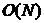 ,而量子搜索算法的复杂度是
,而量子搜索算法的复杂度是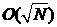 [4],这表明量子搜索算法比相应的经典算法具有平方量级的加速。而且,由于搜索算法本身有着广泛的应用范围,量子搜索算法可以使很多问题更快速地得到解决。这里所提到的两种量子算法,体现了量子计算机的强大运算能力,在国家安全和商业价值方面都具有巨大的潜力。
[4],这表明量子搜索算法比相应的经典算法具有平方量级的加速。而且,由于搜索算法本身有着广泛的应用范围,量子搜索算法可以使很多问题更快速地得到解决。这里所提到的两种量子算法,体现了量子计算机的强大运算能力,在国家安全和商业价值方面都具有巨大的潜力。
1.2 研究现状
目前,量子计算机的研究主要集中解决这两个问题:一是如何实现通用量子计算机;二是如何设计并利用量子算法来解决实际问题。下面分别介绍这两个方面的研究概况。
近二十年来,实验科学家们致力于实现通用量子计算机,尽管目前距离实现这一目标还有很长的路要走,但也取得了许多突破性的进展。2000年,IBM研究中心的David P. DiVincenzo提出了构建量子计算机的判据[5]:(1)系统由可扩展的量子比特构成;(2)量子比特可初始化成简单的基准态(如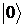 或
或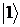 等);(3)系统的相干时间远大于量子门操作时间;(4)通用且完备的量子门操作集;(5)能够准确读取量子比特的态。对于任何量子比特技术,最重要的问题是:物理体系的什么性质可用来表征量子比特的“0”或“1”态[3]?随后,我们才需要考虑初始化、相干时间、量子门、测量等问题。量子计算机中的信息是隐藏在量子比特所处状态的,但量子比特却极易受到噪声的干扰。而真实系统总是存在噪声的,一方面来自外界环境,另一方面来自控制量子比特的仪器[6]。如何保证我们从量子比特中读取的信息尽量准确,则显得尤为重要。目前,普遍采取的思路是,基于量子纠错(QEC)理论来实现容错量子计算机。研究人员已提出多种实现量子容错的方法,但当前最大的研究热点是表面编码(surface code)。此编码方法的特点是:高容错阈值(约
等);(3)系统的相干时间远大于量子门操作时间;(4)通用且完备的量子门操作集;(5)能够准确读取量子比特的态。对于任何量子比特技术,最重要的问题是:物理体系的什么性质可用来表征量子比特的“0”或“1”态[3]?随后,我们才需要考虑初始化、相干时间、量子门、测量等问题。量子计算机中的信息是隐藏在量子比特所处状态的,但量子比特却极易受到噪声的干扰。而真实系统总是存在噪声的,一方面来自外界环境,另一方面来自控制量子比特的仪器[6]。如何保证我们从量子比特中读取的信息尽量准确,则显得尤为重要。目前,普遍采取的思路是,基于量子纠错(QEC)理论来实现容错量子计算机。研究人员已提出多种实现量子容错的方法,但当前最大的研究热点是表面编码(surface code)。此编码方法的特点是:高容错阈值(约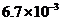 ),近邻量子比特相互作用,简单的错误校正提取线路,一套基于横向门的容错逻辑等[7]。
),近邻量子比特相互作用,简单的错误校正提取线路,一套基于横向门的容错逻辑等[7]。
综合考虑DiVincenzo提出的判据以及实现量子容错的要求,基于超导宏观量子态的超导量子比特系统被认为是最有可能实现容错量子计算机的方案之一,这方面的研究成果也层出不穷。1999年,Y. Nakamura等使用约瑟夫森结将超导电极构造成人工二能级系统,提出电荷量子比特[8];2002年,John M. Martinis等设计了一种基于大面积电流偏置约瑟夫森结的电路,提出Phase量子比特[9];2007年,Koch等提出一种新型量子比特结构(2D)Transmon,与电荷量子比特不同的是,Transmon采用显著增加约瑟夫森能与电荷能比值方法[10];2009年,Manucharyan等提出Fluxonium量子比特,将很多大结串联起来,然后与小的电容并联,很好地解决了电荷量子比特面临的电荷漂移问题[11];2013年,R. Barends等设计了一种可以降低辐射损失和缺陷耦合的几何结构,提出了Transmon的变异体Xmon量子比特[12];2016年,Yan等在磁通量子比特上并联了一个电容,提出一种命名为C-shunt flux qubit (CSFQ)的改进型磁通量子比特结构[13]。这些新型量子比特结构的提出,使得超导量子比特多方面的性能参数逐步得到提升,以退相干时间为例,该参数就实现了近6个数量级的提升。超导量子比特的飞速发展,自然推动了超导量子芯片的相关研究。2007年,J.Majer等利用传输线腔中的微波光子实现了量子总线(quantum bus),并用它耦合芯片中的两个超导量子比特[14];2014年,R. Barends等演示了多比特超导处理器中的一组通用逻辑门,实现了99.92%保真度的单比特门和99.4%保真度的两比特门[15];2017年,Abhinav Kandala等在由Transom量子比特构成的量子芯片上设计出变分量子本征值求解器,从实验上优化哈密顿问题,确定了不同大小分子的基态能量[16]。
以上是毕业论文大纲或资料介绍,该课题完整毕业论文、开题报告、任务书、程序设计、图纸设计等资料请添加微信获取,微信号:bysjorg。
相关图片展示:


课题毕业论文、开题报告、任务书、外文翻译、程序设计、图纸设计等资料可联系客服协助查找。



