基于细观方法的各向同性磁流变弹性体磁致模量分析毕业论文
2020-04-12 16:09:47
摘 要
磁流变弹性体是将磁性颗粒与高聚合物混合固化后形成的一类新型的智能复合材料,其力学性能可由外磁场控制,因此广泛应用于主动控制器件中,如运载工具的主动控制阻尼器、减噪器等。
本文考虑到各向同性磁流变弹性体(Magnetorheological Elastomers简称MREs)中存在的铁磁颗粒的空间位置存在随机分布的现象,假设相邻铁磁颗粒的间距满足对数正态分布,对磁流变弹性体的偶极子模型进行了修正,分析了各向同性随机颗粒分布情形下的磁流变弹性体磁致剪切模量并给出了磁致剪切模量的表达式。通过修正描述磁致颗粒空间相对位置的磁偶极子模型,更为精确地分析了各向同性磁流变弹性体的磁致剪切性能。该修正模型不仅能够对铁磁颗粒随机分布下的非耦合磁流变弹性体剪切模量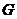 予以预测,给出其磁致剪切模量的概率密度分布的特征,并能够预测各向同性磁流变体的磁致剪切模量
予以预测,给出其磁致剪切模量的概率密度分布的特征,并能够预测各向同性磁流变体的磁致剪切模量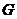 与空间位置的关系;同时该模型还可以在剪切方向固定时退化为传统偶极子模型,并可模拟颗粒链斜向分布时,磁流变弹性体的磁致剪切模量。
与空间位置的关系;同时该模型还可以在剪切方向固定时退化为传统偶极子模型,并可模拟颗粒链斜向分布时,磁流变弹性体的磁致剪切模量。
本文重点考虑了材料颗粒空间位置角度与颗粒间距这两种细观因素存在的随机性,为了精确描述磁流变弹性体的磁致效应,引入分布参量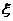 ,
,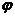 ,
,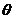 ,
, 来确定磁流变弹性体中任意相邻颗粒间的空间位置,基于磁偶极子理论,修正了磁流变弹性体的磁致模量的表达形式,引入概率统计的方法,理论分析了随机颗粒尺寸或间距下的磁流变弹性体磁致剪切模量的概率密度函数,一定程度上揭示了磁流变弹性体局部磁致剪切模量与这两种因素随机性间的规律。本文研究在一定程度丰富了各向同性磁流变弹性体磁致性能的理论分析基础,对各向同性磁流变弹性体中存在剪切模量分布不均匀的现象予以的合理解释。
来确定磁流变弹性体中任意相邻颗粒间的空间位置,基于磁偶极子理论,修正了磁流变弹性体的磁致模量的表达形式,引入概率统计的方法,理论分析了随机颗粒尺寸或间距下的磁流变弹性体磁致剪切模量的概率密度函数,一定程度上揭示了磁流变弹性体局部磁致剪切模量与这两种因素随机性间的规律。本文研究在一定程度丰富了各向同性磁流变弹性体磁致性能的理论分析基础,对各向同性磁流变弹性体中存在剪切模量分布不均匀的现象予以的合理解释。
关键词: 磁流变弹性体;偶极子模型;随机颗粒分布;磁致剪切模量
Abstract
Magnetorheological elastomer is a kind of new intelligent composite material formed by mixing and solidifying magnetic particles and high polymer. Its mechanical properties can be controlled by external magnetic field, so it is widely used in active control devices, such as active control damping of vehicles Device, noise reducer, etc.
This paper considers the existence of random distribution of ferromagnetic particles in isotropic magnetorheological elastomers (MREs), assuming that the spacing between adjacent ferromagnetic particles satisfies the lognormal distribution, and the magnetic flux The modified dipole model of the elastomer was modified to analyze the magnetohydrodynamic shear modulus of the magnetorheological elastomer with isotropic random particle distribution and the expression of the magnetostrictive modulus was given. By correcting the magnetic dipole model describing the relative position of the magnetic particles, the magnetic shear properties of isotropic magneto-rheological elastomers are analyzed more precisely. The modified model can not only predict the shear modulus of the uncoupled magnetorheological elastomer with random distribution of ferromagnetic particles, but also give the characteristics of the probability density distribution of the magnetic shear modulus, and can predict the isotropic magnetic properties. The relationship between the magnetic shear modulus and the spatial position of the rheological body; at the same time, the model can also degenerate into a traditional dipole model when the shear direction is fixed, and can simulate the oblique distribution of the particle chain, the magnetorheological elastomer The magnetic shear modulus.
This paper focuses on the randomness of the two mesoscopic factors: the spatial position angle of the material particle and the particle spacing. In order to accurately describe the magnetic induced effect of the magnetorheological elastomer, the distribution parameters are introduced to determine the magnetorheological elastomer. The spatial position between any adjacent particles, based on the theory of magnetic dipoles, modifies the expression form of the magnetic modulus of the magnetorheological elastomer and introduces the method of probability statistics to theoretically analyze the magnetic flow at random particle size or spacing. The probability density function of the magnetostrictive shear modulus of the variable elastomer reveals to a certain extent the local magnetic shear modulus of the magnetorheological elastomer and the randomness of these two factors. This paper studies the theoretical analysis basis of the magnetic properties of isotropic magneto-rheological elastomers to a certain extent, and provides a reasonable explanation for the presence of non-uniform shear modulus distribution in isotropic magneto-rheological elastomers.
Key Words:Magnetorheological elastomer;Dipole model;
Random particle distribution;Magnetic shear modulus
目 录
摘 要 I
Abstract II
第1章 绪论 1
1.1 研究背景和发展现状 1
1.1.1磁流变弹性体的磁弹性行为研究 1
1.1.2磁流变弹性体磁弹性行为分析与磁偶极子模型 1
1.2研究意义 3
1.3本文工作 3
第2章 各向同性磁流变弹性体偶极子概率模型 5
2.1磁偶极子理论 5
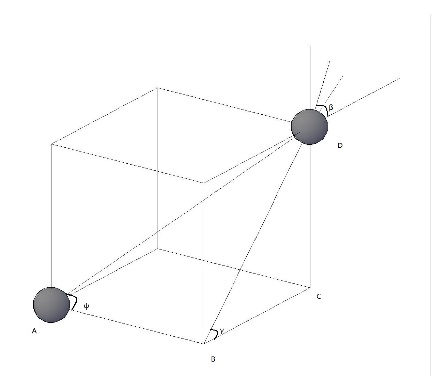
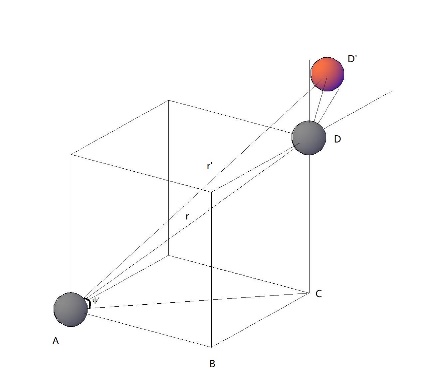
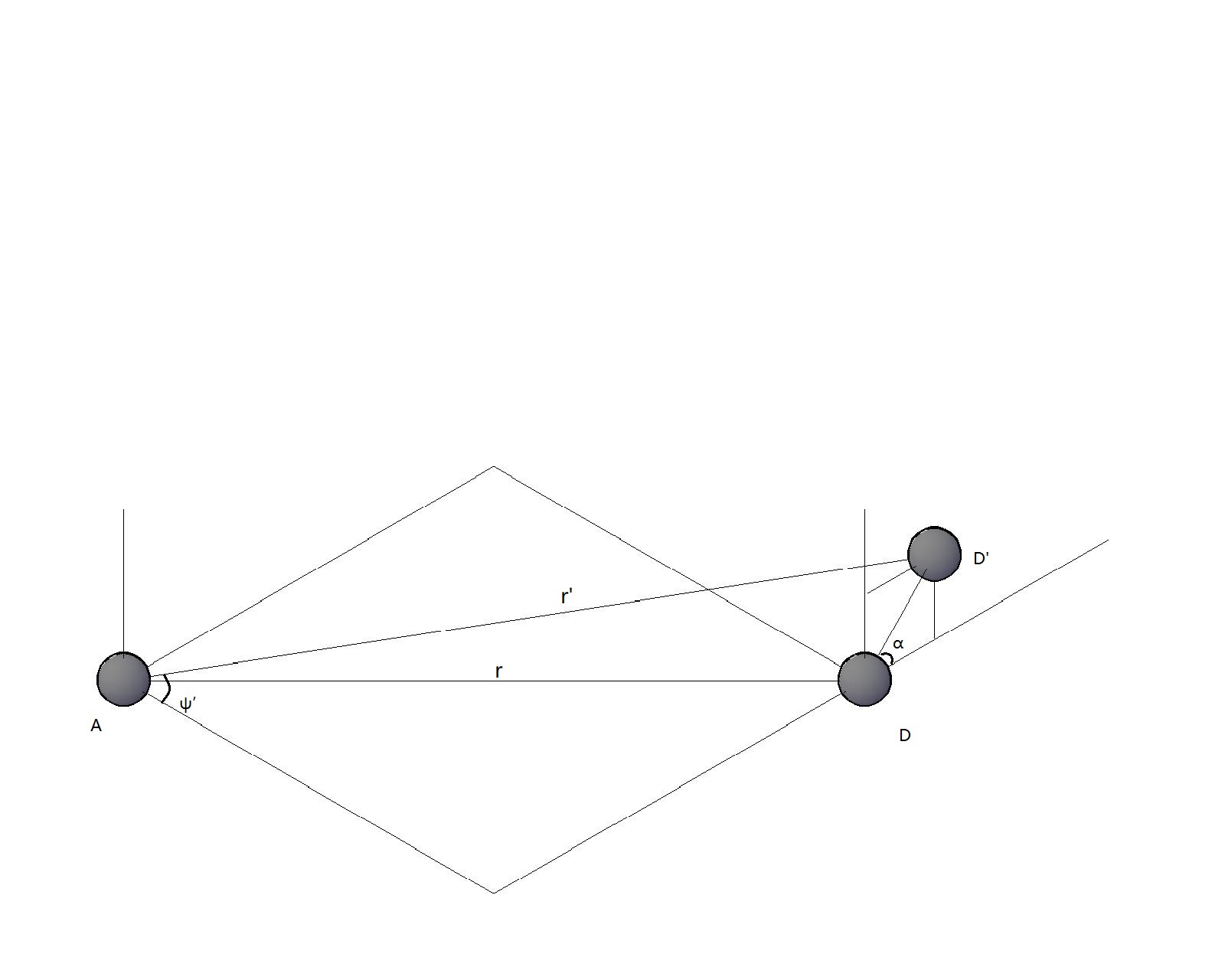
2.2偶极子模型的建立 5
2.3 两种描述粒子空间位置的偶极子模型 6
2.3.1 一种用以描述磁致颗粒空间位置的磁偶极子模型 7
2.3.2 简化参量后的修正模型 10
第3章 各向同性磁流变弹性体磁致模量的不均匀性分析 14
第4章 数值结果及讨论 17
结论 19
参考文献 20
致谢 22
第1章 绪论
1.1 研究背景和发展现状
随着现代工业的迅猛发展和科学技术的快速进步,诸多智能材料被陆续研发出来并应用于各领域中,其中磁流变材料因具有优秀的磁流变效应而受到广泛的关注。磁流变弹性体(Magnetorheological Elastomers, 简称MREs)作为磁流变材料家族中的一员,是将高磁化率的铁磁性微小颗粒嵌入较软的聚合物基体中,通过外加磁场或无磁场情形下固化制备出的具有某种特定细观结构的智能颗粒夹杂复合材料。磁流变弹性体材料兼容了力学、磁学和电学等多场相互控制的特性,因此有着更为广泛的应用前景[1]。磁流变弹性体作为磁流变液的一种派生材料,较磁流变液的最大优势在于颗粒不会随时间而沉降,同时也不需要在磁流变材料的使用过程中,随时保持工作位置的密封性,这使得对磁流变弹性体材料的研究受到国内外工业界和学术界的普遍关注。
1.1.1 磁流变弹性体的磁弹性行为研究
针对磁流变弹性体的研制与性能研究已有二十余年的历史,自1990年此类材料呈现出在磁场下独特的粘弹性特性,陆续有学者开展了这方面的研究,至今保持了很高的热度。Lord公司的研究人员Jolly、Carlson等人[2]初步测试和分析了磁流变弹性体的力学性能,其制备的磁流变弹性体剪切模量初始值在0.8T的外场下比无磁场时增加约40%;随后,Ginder等人[3]对天然橡胶基的磁流变弹性体进行了建模分析,研究了其粘弹性行为。近年来,Johnson等人[4]通过实验和理论研究,研究了磁流变弹性体的动态剪切特性,分析了磁弹性体中颗粒体积比对材料性能的影响。Molchanov等人[5]通过对应力控制流变仪的各种振幅进行动态剪切振动的研究,对磁弹性体的粘弹性特性进行了研究并且在垂直于剪切面上的磁场中,对材料的磁致响应进行了分析。Qi等人[6]进行了磁流变弹性体的应力松弛行为的实验和建模研究,发现其应力松弛行为依赖于所处的磁场和温度环境。
1.1.2 磁流变弹性体磁弹性行为分析与磁偶极子模型
磁流变弹性体由于外部磁场环境作用,其内部磁性颗粒将产生强烈相互作用:一种空间长程电磁力作用,进而带动周围基体产生形变;由于基体相对较软,材料整体上表现出显著的超磁致伸缩性。磁流变弹性体不仅在模量与阻尼磁场可控性上表现出优异的性能,而且表现出优秀的超磁致伸缩行为。为了分析磁流变弹性体的磁流变行为,早期学者们运用磁偶极子模型,开展了一系列的理论分析工作。他们将单一颗粒视为一个磁偶极子,在磁场的作用下颗粒因磁化而出现相互作用,磁偶极子的相互作用能反映出这一作用。该模型是研究磁流变液等材料磁控剪切性能时较为观有效的方法,因此被沿用下来分析磁流变弹性体的磁控性能。Jolly、Davis和Shen等人[7,8,9]均从磁偶极子理论出发,结合相关实验,进行了对磁流变弹性体磁控性能的解释性工作:Jolly[7]将弹性体中近似链状的颗粒结构视为是理想的平行结构,建立了磁流变弹性体磁偶极子模型,预测了磁致剪切模量的变化。Davis[8]采用磁偶极子理论分析了加入铁磁颗粒前后材料的力学行为的变化,给出了最佳体积分数的概念以及预测了相对磁致剪切模量的最大值。Shen等人[9]考虑了链内的颗粒在外加磁场中自身磁极化产生磁场,建立了磁偶极子耦合物理场模型,较为精细地预测了磁致剪切模量。Hong等人[11]发现磁流变弹性体中会出现有限长颗粒链,结合颗粒链分布特征,基于磁偶极子理论,开展了对磁流变弹性体的磁控力学性能的理论分析工作。Diguet等人[12]从磁偶极子相互作用的角度,理论解释了磁流变弹性体磁致伸缩效应的原因。重庆大学的余淼等人[13]将铜线圈绕制在磁流变弹性体的内部,研究了其力学性能;而且运用磁偶极子模型分析了磁流变弹性体磁控特性。Yin等人[14,15]运用该方法分析磁流变弹性体内部颗粒的平均磁场,通过计算两个颗粒间的相互作用力,结合细观力学方法得出的材料各向异性模量,等效获得磁流变弹性体的磁致模量。在细观力学理论的分析过程中,颗粒与基体的弹性作用可以由颗粒间的相互作用来等效表出。Ausanio等人[16]研究了外部磁场作用下磁流变弹性体的相对弹性变形及其与磁矩和内部弹性力矩之间的平衡关系。Lanotte等人[17]在假定磁流变弹性体中颗粒均匀分布的基础上研究了因存在扭矩而发生粒子旋转的磁流弹性体的磁致特性。Coquelle等人[18]在准静态建模中考虑了颗粒之间的间隙,应用有限元方法研究了无磁场时单轴张力状态下的磁流变弹性体的磁致响应,该模型的基础。党辉等人[19]在考虑磁流变弹性体中链的方向分布的基础上,对磁流变弹性体的偶极子模型作出了修正.用局部场的方法计算了链的势能,引入了分布函数来描述链的分布,并分析了与磁场方向不一致的斜链的磁流变效应,进而通过积分叠加求得 含有分布链的磁流变弹性体的磁流变效应.在磁流变弹性体的理论模型中,引入了制备磁场和基体性质等影响因素,结果表明磁流变弹性体内铁磁颗粒链方向与外加磁场方向趋于一致的可能性最大。朱应顺等人[20]提出了磁流变弹性体的柱状和层状结构模型,预测得到了层状对应的磁致剪切模量要高于相同颗粒体积分数下的链状结构的磁流变弹性体;Zhang等人[21]分析了铁磁颗粒体心立方结构分布的磁流变弹性体,基于磁偶极子理论分析了相应的力学性能。
通过Kankanala等人的理论工作可以发现,磁流变弹性体的宏观理论建模可以借鉴已经发展的较为成熟的磁弹性理论。用于分析均匀电磁介质的电磁弹性力学理论已经发展了近半个世纪,目前国际上比较认可的成熟理论模型有:基于磁偶极子物理理论建立起的磁体力偶模型(Moon-Pao,1968),基于公理化方法建立的磁弹性力学模型(Pao-Yeh,1973),基于理性力学方式建立的磁弹性力学模型(Eringen-Maugin,1980),基于Maxwell应力张量的变分原理模型(van de Ven, 1984)。国内兰州大学的Zhou与Zheng建立了弹性材料的磁体力模型和基于广义变分原理获得材料磁体力的磁弹性力学模型。
以上是毕业论文大纲或资料介绍,该课题完整毕业论文、开题报告、任务书、程序设计、图纸设计等资料请添加微信获取,微信号:bysjorg。
相关图片展示:
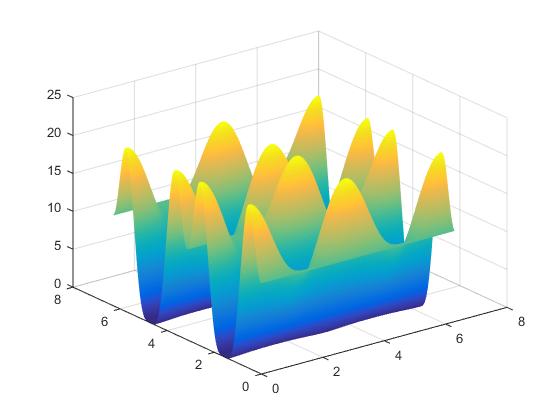
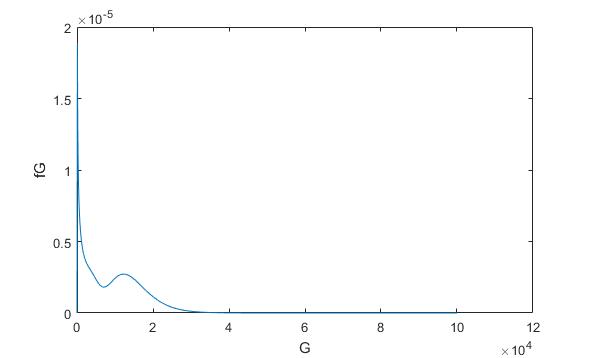
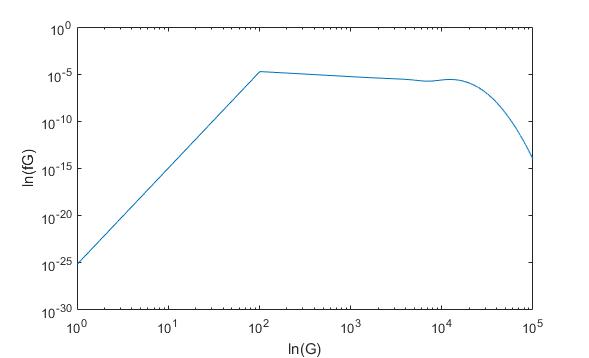
课题毕业论文、开题报告、任务书、外文翻译、程序设计、图纸设计等资料可联系客服协助查找。



