数据驱动的微分方程学习:稀疏优化方法毕业论文
2020-04-24 11:15:08
摘 要
微分方程提供了物理和生命科学的基本模型,在数学领域,对微分方程的研究着重在几个不同的方面,但大多数都是关心微分方程的解,然而只有少数简单的微分方程可以求得解析解。虽然根据观测数据求得微分方程模型和参数较为困难,但是随着科学技术的发展,数据驱动的发现方法进入人们的视线并为研究大型数据集和学习提供了数值工具。这些方法可以为研究人员提供重要的技术来支持和扩大他们的科学发现之路。
本文首先介绍了从稀疏编码中发现偏微分方程的过程,并举伯格斯方程的例子具体介绍。之后详细介绍稀疏优化算法以及用多项式插值法计算导数的过程。接着,用三个仿真例子验证该方法,得出该方法的实用性和一些局限性。
该方法具有计算效率高、鲁棒性强的优点,并被证明适用于包括纳维-斯托克斯、量子谐振子和扩散方程在内的多个科学领域的各种典型问题。此外,该方法还可以通过使用不同初始数据的多个时间序列来消除潜在的非唯一动态项之间的歧义。该方法为参数化时空系统的控制方程和物理规律的发现提供了一种很有前途的新技术。
关键词:数据驱动 偏微分方程 稀疏优化算法
Data-driven differential equation learning: sparse optimization methods
Abstract
Differential equation provides the basic model of physics and life science. In the field of mathematics, the study of differential equation focuses on several different aspects, but most of them are concerned with the solution of differential equation. However, only a few simple differential equations can be solved analytically. Although it is difficult to obtain differential equation models and parameters based on observation data, with the development of science and technology, data-driven discovery methods come into people's attention and provide numerical tools for studying large data sets and learning. These methods can provide researchers with important technologies to support and expand their path to scientific discovery.
This paper first introduces the process of finding partial differential equations from sparse coding, and gives an example of burgess equation. Then the sparse optimization algorithm and the process of calculating the derivative with polynomial interpolation method are introduced in detail. Then, three simulation examples are used to verify the method, and the practicability and some limitations of the method are obtained.
This method has the advantages of high computational efficiency and strong robustness, and has been proved to be suitable for many typical problems in many scientific fields, including navier-stokes, quantum harmonic oscillator and diffusion equation. In addition, this method can eliminate the ambiguity between potential non-unique dynamic items by using multiple time series of different initial data. This method provides a promising new technique for the discovery of governing equations and physical laws of parametric space-time systems.
Keywords: Data-driven; Partial differential equation; Sparse optimization algorithm
目 录
第一章 引言 4
1.1 研究背景和意义 4
1.2 研究现状 4
1.3 本文的方法概述 5
第二章 基于稀疏编码发现偏微分方程 6
2.1 模型 6
2.1.1 伯格斯方程 7
2.2 稀疏优化算法 8
2.2.1 偏微分方程稀疏回归 9
2.3 数值求导 11
2.3.1 拉格朗日插值 11
2.3.2 切比雪夫多项式 12
第三章 实验仿真 13
3.1发现Navier-Stokes方程 13
3.2 传感器的动态运动 14
3.3 消除动态系统 15
第四章 总结与展望 17
4.1 总结 17
4.2 展望 17
参考文献 19
致谢 21
第一章 引言
1.1 研究背景和意义
数据驱动的发现方法在过去十年中由于传感器、数据存储和计算资源成本的急剧下降而得以实现,它对科学产生了革命性的影响,促进了对实验产生的高维数据进行表征的各种创新。对于如何从表现出时空活动的时间序列数据中发现潜在的物理规律和/或控制方程,人们知之甚少。传统的推导偏微分方程的理论方法植根于守恒定律、物理原理和/或现象学行为。这些基本原理的推导导致了物理、工程和生物科学中普遍存在的许多规范模型。然而,仍然有许多复杂的系统无法对适当的变量选择(例如,神经科学、电网、流行病学、金融和生态学)进行定量分析描述甚至特征描述。本文的方法根据在固定数量的空间位置收集的时间序列数据导出控制方程。利用稀疏回归的创新,我们发现了最准确地表示来自大量潜在候选函数库的数据的控制偏微分方程的项。测量可以在欧拉框架中进行,其中传感器在空间上是固定的,或者在拉格朗日框架中,传感器随动力学运动。我们通过仅仅从时间序列数据中重新发现大量的物理规律,证明了该方法的成功。
1.2 研究现状
动力系统数据驱动发现的方法[1]包括无方程建模[2]、人工神经网络[3]、非线性回归[4]、经验动态建模[5,6]、正态识别[7]、非线性拉普拉斯光谱分析[8]、紧急行为建模[9]和动力学自动推理[10-12]。在这一系列的发展中,开创性的贡献利用符号回归和进化算法[13,14]能够直接从数据中确定非线性动力系统。近年来,稀疏性[15]被用来以一种高效的计算方式稳健地确定控制动力系统[16,17]。进化[14]和稀疏[16]符号回归方法都通过选择通过帕累托分析平衡模型精度和复杂性的简约模型来避免过度拟合。本文的方法能够从一个大的库中选择正确的线性、非线性和空间导数项,从而从数据中识别偏微分方程。只有那些最能提供动力学信息的项才被选为所发现的偏微分方程的一部分。这里提出的创新非常重要,因为它有效地处理时空数据,这是许多规范模型的基本特征。以往的稀疏促进方法能够从数据中识别常微分方程(ode),但不能处理时空数据或高维测量[16]。本文的方法有几个有利的实际特点:测量可以在固定或移动的框架(欧拉或拉格朗日)中收集,允许广泛应用于各种实验数据;该算法还可以通过创新的采样策略有效地处理高维数据。该算法,即非线性动力学的偏微分方程泛函辨识(PDE- find),被广泛应用于规范模型中。
1.3 本文的方法概述
本文首先介绍了从稀疏编码中发现偏微分方程的过程。之后详细介绍稀疏优化算法以及用多项式插值法计算导数的过程。接着,用三个仿真例子验证该方法,得出该方法的实用性和一些局限性。
基于稀疏编码发现偏微分方程
2.1 模型
本文考虑了一般形式的参数化非线性偏微分方程
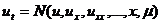 (2.1.1)
(2.1.1)
课题毕业论文、开题报告、任务书、外文翻译、程序设计、图纸设计等资料可联系客服协助查找。



